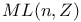Global symmetry group of a point set 194
Globally fixed geometrical invariant 153
Goursat's Rule for constructing subdirect products 317
Goursat's theorem 65
Greek element of a direct product group 60 436
Grey space group 361
Group 8 10
Group action = action of a group 44
Group of a J-vector 397
Group of a P-vector 397
Group of affine transformations referred to a coordinate system 117 122
Group of all affine transformations of an affine space = affine group 110
Group of all isometries of a Euclidean point space = Euclidean group 115
Group of all translations of an affine space 111
Group of an M-vector 397
Group of antisymmetry 358
Group of automorphisms of a complex vector space 523
Group of automorphisms of a group 45
Group of cambiant symmetry 360
Group of isometries = subgroup of a Euclidean group
Group of linear and antilinear transformations 526
Group of linear transformations referred to a basis 107
Group of permutations 14
Group of permutations generated by a subgroup 68
Group of permutations of a set 32
Group of primitive translations 259
Group of proper and improper rotations 62 201
Group of rotations at a point 116 148 149 163
Group of rotations of a plane 162
Group of rotations of space = point group 149
Group of rotations of space-time = subgroup of the space-time rotation group 169
Group of rotations of the first kind 156
Group of rotations of the second kind with inversion 156
Group of rotations of the second kind without inversion 156
Group of symmetry and antisymmetry 361
Group of transformations of a set onto itself 32
Group of various kinds of antisymmetry 360
Group product = product of elements of a group
H-M symbols = Hermann — Mauguin symbols
h-subgroup 62
Handedness = orientation 119
Heesch group = crystallographic group of space-time rotations 174 361 394 573
Heesch group compatible with a crystalline medium 498
Heesch — Shubnikov group 356 361 N12.8
Helical group 153 195 332 Nll.l
Helical spin arrangement 489
Helix, irrational discrete 336
Helix, rational discrete 336
Hemisymmorphic space group N9.3
Hermann — Mauguin symbols (= H-M symbols = international symbols), full and short 0
Hermann — Mauguin symbols for the Bravais subclasses of an affine class of space groups 273
Hermann — Mauguin symbols for the groups of rotations in a plane 163 164 T6.7
Hermann — Mauguin symbols for the line groups in a plane 312 Tll.1.1 Tll.1.2
Hermann — Mauguin symbols for the line groups of space 325
Hermann — Mauguin symbols for the magnetic groups of rotations (= magnetic point groups) 408
Hermann — Mauguin symbols for the net groups of space 312 T11.2
Hermann — Mauguin symbols for the one-dimensional space groups 274
Hermann — Mauguin symbols for the three-dimensional magnetic space groups M of the kind 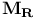 450 450
Hermann — Mauguin symbols for the three-dimensional magnetic space groups M of the kind 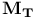 442 442
Hermann — Mauguin symbols for the two- and three-dimensional space groups 279 280 281
Hermann — Mauguin symbols for the two-dimensional magnetic space groups 224
Hermann — Mauguin symbols, modified, for the groups of rotations of space 158 T6.5
Hermann — Mauguin symbols, modified, for the subgroups of the space-time rotation group 170 T6.8 T6.9
Hermann — Mauguin symbols, standard, for the groups of rotations of space 155 158 T6.5
Hermann — Mauguin symbols, standard, for the subgroups of the space-time rotation group 170 T6.8 T6.9
Hermann's Theorem 260
Hermitian adjoint of a matrix 77
Hermitian form associated with a basis of a unitary vector space 521
Hermitian inner product (= scalar product) of two vectors 520 521
Hermitian matrix 77
Hexagonal Bravais system of point lattices (two- and three-dimensional) T8.2 T8.3
Hexagonal Bravais system of space groups (two- and three-dimensional) T9.1.3 T9.2.3
Hexagonal geometric-class system of groups of rotations (of a plane and of space) T6.2 T6.5 T6.7
Hexagonal groups of rotations (of a plane and of space) T6.2 T6.5 T6.7
Hexagonal ITC-system of space groups (two- and three-dimensional) T9.1.3 T9.2.2
Hexagonal point lattice (two- and three-dimensional) 234 243 244
Hilbert space N21.2
Him G 50
Holohedral class of groups of rotations 216 T6.2
Holohedral group of rotations 216
Holohedral matrix group 217
Holohedry of a magnetic point lattice 422
Holohedry of a magnetic point lattice at one of its points 422
Holohedry of a point lattice 216
Holohedry of a point lattice at a point 215
Holomorph of a group 45 50
Homogeneity of a transitive set 39
Homomorphism of a group into a group 23
Homomorphism of a group onto a group 22
Homomorphism theorem 23
Homomorphisms with the same kernel 50
I-groups of space-time rotations 156 168 173 T6.8
Icosahedral group (= dodecahedral group) of proper rotations 21 156 408 Npr
Ideal crystal 293
Identification 358
Identity automorphism 45 52
Identity element (= unit element) of a group 10
Identity permutation 31
Identity permutation representation of a group 70
Identity representation of a group 24 135
Identity rotation 13
Image of a group Npr
Image of a homomorphism 23
Image of an element of a set under a mapping 5
Image of an irreducible representation of a group Npr
Imperfect crystal 355
Improper motion = opposite isometry 121
Improper rotation 116 121 148 150 162
Improper subgroup 15
Incommensurate crystal 197 537
Incommensurate modulated point lattice 539
Indecomposable constituents of a matrix group 134
Indecomposable discrete group of isometries = space group 187 196 N7.7
Indecomposable matrix group 132 133
Indecomposable representation of a group 135
Index 2 Lemma 29
Index of a subgroup 19
Index-2 subgroups of a lattice group 414 417 T16.1 T16.2
Inducing a linear transformation by an affine transformation 110
Inequivalent matrix groups 76
Inequivalent matrix representations 135
Infinite axial group of rotations 160 T6.6
Infinite group 11
Infinite index of a subgroup 19
Infinite subgroups of the affine group T4.1
Infinite-dimensional (complex or real) vector space 89 N21.2
Inhomogeneous linear transformation 112 N4.2
Inhomogeneous Lorentz group = Poincare group N6.5
Inhomogeneous orthogonal-matrix group 116
Inhomogeneous rotation-matrix group associated with a basis 116
Injection 5
Inn G 46
Inner automorphism 46
Inner product (= scalar product) of two vectors 95 519
Inner product of two rays 521
Instant 87 101 165
Integral linear combination of lattice vectors 202
Integral matrix 79
Integral matrix group = subgroup of 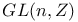 \mathbb \mathbb
Internal semidirect product of groups 56
International symbols = Hermann — Mauguin symbols 158
Intersection of two groups 16
intersection of two sets 3
Intransitive group of permutations 39
Intransitive set 39
Invariance group of a function 44
Invariance group of a magnetic dipole arrangement = - a spin arrangement
Invariance group of a physical crystal 381
Invariance group of a point set 191
Invariance group of a spin arrangement 400
| Invariance group of a subset 37 38
Invariance group of an atomic system 529 530
Invariance group of an electric dipole arrangement 408
Invariance group of the constitutive relations 397
Invariance of a point set under an isometry 191
Invariance of a subset under a permutation 37
Invariant spin arrangement N18.2
Invariant spin of a magnetic site group 478
Invariant spin of a magnetically admissible group of rotations T18.1
Invariant subgroup = normal subgroup 47
Invariant subspace of a carrier space 138
Invariant vector of a group in a carrier space 138
Inverse of a permutation 31
Inverse of an element of a group 10
Inversion = space inversion 150 152 167
Inversion group 151
Inversion group of a line 165
Inversion point 151
Irrational angle 161
Irrational discrete helix 336
Irrational helical spin arrangement 489 N18.5
Irrational lattice group 550
Irrational point lattice 550
Irrational standard basis 550
Irreducible carrier space 138
Irreducible constituents of a matrix group 134
Irreducible matrix group 132 135
Irreducible representation of a group 135
Irreducible representations of the dihedral group T5.1
Iso G 49
Isometric Euclidean point spaces 127
Isometric Euclidean vector spaces 127
Isometry group = Euclidean group 103
Isometry of a Euclidean point space 115 116
Isomorph of a group 45 47
Isomorphism class of crystallographic groups of rotations of space T6.3
Isomorphism class of groups 8 14
Isomorphism class of groups of isometries 123
Isomorphism class of space groups 123 262
Isomorphism of affine spaces 93
Isomorphism of groups 14
Isomorphism of vector spaces 90
IT-number of a space group 272
ITC = either ITC 52 or ITC 83
ITC 52 = International Tables for X-Ray Crystallography, Vol. I 158 197
ITC 83 = International Tables for Crystallography, Vol. A 158 197
ITC-system of affine classes of space groups 277
ITC-system of arithmetic classes of space groups 277
ITC-system of geometric classes of space groups 277
J-Heesch group 397 T19.1
J-Heesch — Shubnikov group 494
Jacobi matrix 100 125 T3.1
Jacobi transformation 100 N3.4
JM-Heesch group 397 T19.1
Jordan's Theorem 222 268 N8.5
JP-Heesch group 397 T19.1
Junior group of symmetry and antisymmetry 361
K-class of simple point sets 294
K-orbit of a point 189
Kernel of a homomorphism 23
Klassengleiche Untergruppe = R-subgroup 261
Kramers operator 531 N21.6
Kronecker product (= direct product) of matrices 143
Kronecker product (= direct product) of matrix representations 143 145
Kronecker symbol 36
Lagrange's theorem 19
Latin element of a direct product group 60 436
Lattice = point lattice
Lattice group 187 195 201
Lattice line 201
Lattice of a Bravais superspace group 552
Lattice of a magnetic space group 439
Lattice of a space group 250
Lattice of an infinite decomposable group of isometries 306
Lattice plane 201
Lattice point 201
Lattice vector 201
Layer group = net group
Leader of a Bravais flock 227 240 269
Left cosets of a subgroup 8 19
Left-coset array for a site group of a space group 291 T10.1.1
Left-handed coordinate systems 120
Length of a translation 116
Line = one-dimensional Euclidean point space 164
Line group 196 306 N7.4 Nll.l
Line group as a subgroup of a two-dimensional space group 313
Line group associated with a pair of quotient groups 320 T11.4
Line group associated with a two-dimensional group of rotations and a one-dimensional space group 316
Line group in a plane 311 Tll.l
Line group in space 311 T11.5
Line in an affine space 93
Linear combination of vectors 89
Linear component of a rigid motion N4.4
Linear constituent of a rigid motion N4.4
Linear group of a vector space 103 104
Linear independence of vectors 89
Linear part of an affine transformation 113 128
Linear part of an element of a magnetic space group 439
Linear part of an element of the Newton group 166 438
Linear part of an isometry 116 128 N4.4
Linear transformation of a vector space 104 113
Linearly independent translations 115
Local symmetry group of a point set 194
Local symmetry of a point set 194
Lorentz equations 398
Lorentz group (inhomogeneous) = Perineal group N6.5
M-Heesch group 397 T15.3 T19.1
M-Heesch-Shubnikov group 494
Macromolecule 196 328
Macroscopic field equations of Maxwell 394 398
Magnetic basis of a magnetic lattice group 418 T16.2
Magnetic basis of a magnetic point lattice 422 T16.2
Magnetic Bravais class 423
Magnetic charge density 396 N16.3
Magnetic coordinate system for a magnetic lattice group 418
Magnetic coordinate system for a magnetic point lattice 422
Magnetic crystal 475
Magnetic dipole arrangement (— spin arrangement) 355
Magnetic dipole moment 349
Magnetic families of the groups 422
Magnetic families of the groups; 4mm; 42m T15.1
Magnetic family of a group of isometries 404
Magnetic family of a lattice group 417
Magnetic family of the group 4/mmm T15.2
Magnetic field strength 394
Magnetic group 62 356 357 375
Magnetic group (Definition (D2)) 402 N15.2
Magnetic group (Definition (Dl)) 401 N15.2
Magnetic group corresponding to a two-colour group 375 406
Magnetic group of rotations = magnetic point group 401 406
Magnetic induction 394
Magnetic lattice group 401 406
Magnetic lattice group coholohedral with a lattice group 422
Magnetic line group 401
Magnetic linear group 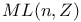 419 N16.2 419 N16.2
Magnetic net group 401
Magnetic order 490
Magnetic point group = magnetic group of rotations 401 406
Magnetic point lattice 420
Magnetic point lattice generated by a magnetic lattice group 420
Magnetic site group 477
Magnetic site point group 477
Magnetic space group 359 401
Magnetic space group, one-dimensional 437 T11.1.1
Magnetic space group; 2-dimensional 437 T11.2
Magnetic space group; 2-dimensional, corresponding to a net group 436
Magnetic space group; 2-dimensional, corresponding to a two-colour space group 436
Magnetic space group; 3-dimensional, corresponding to a two-colour three-dimensional space group 437
Magnetic space group; 3-dimensional, of the kind 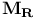 436 438 436 438
Magnetic space group; 3-dimensional, of the kind 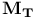 436 438 436 438
|
 |
|
О проекте
|
|
О проекте



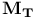
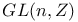 \mathbb
\mathbb