|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Miklowitz J. Ч The theory of elastic waves and waveguides |
|
|
 |
| ѕредметный указатель |
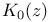 function, integral representation for 329 function, integral representation for 329
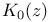 function, Lapwood's integral representation for 330 function, Lapwood's integral representation for 330
Acceleration 43
Acoustics 17
Additional effects 576Ч578
Airy function 388 423 429 438
Airy function, derivatives of 437
Amplitude of P wave 121
Amplitude of SH wave 154
Amplitude of SV wave 121
Amplitude ratios see Reflection coefficients; Transmission coefficients
Analytical continuation of functions, use of 286
Angle, critical 132 139Ч144 163Ч164
Angle, incident 120Ч121 155Ч156
Angle, reflection 120Ч131 155Ч156
Angle, refraction 157 161 165
Anharmonic overtones, infinite plate See Modes thickness
Anisotropic media, for Lamb's problem of a transversely isotropic half space 576
Anisotropic media, for waveguides 576
Anisotropic media, recent work, surveys on 576
Anisotropic media, surfaces of 3
Anisotropic media, waves in, early work, surveys on 576
Anomalous dispersion 187
Anomalous dispersion in transient response of a plate 421
Antiplane, displacement source problem, infinite solid 363Ч364
Antiplane, displacement-potential relations of 153 154
Antiplane, gauge condition in 153
Antiplane, SH waves of 152Ч156 170Ч174
Antiplane, shear deformation 152. See also SH wave Wave
Antiplane, strain-potential relations of 154
Antiplane, stress-potential relations of 154Ч155
Antiplane, tangential surface load problem, half space 363
Antisymmetric edge load problems, plate, rod, semi-infinite 435
Antisymmetric edge load problems, plate, semi-infinite 435
Antisymmetric line loads, problem of, plate, infinite 429Ч430
Approximate theories, waveguide See Waveguides approximate
Asymptotic expansions 250Ч277
Asymptotic expansions of integrals 255Ч277
Asymptotic expansions of integrals, integrals in 256
Asymptotic expansions of integrals, integrals in, critical points of 256
Asymptotic expansions of integrals, integrals in, Fourier 256
Asymptotic expansions of integrals, integrals in, integrand conditions of 256
Asymptotic expansions of integrals, integrals in, Laplace 256
Asymptotic expansions of integrals, methods for, Cagnard Ч deHoop technique, method in, applications of 319Ч323 438Ч443
Asymptotic expansions of integrals, methods for, Laplace's method 262Ч264
Asymptotic expansions of integrals, methods for, Laplace's method, applications of 268 325;
Asymptotic expansions of integrals, methods for, parts integration 257 261Ч262
Asymptotic expansions of integrals, methods for, parts integration, application of 251
Asymptotic expansions of integrals, methods for, stationary phase, method of 271Ч275
Asymptotic expansions of integrals, methods for, stationary phase, method of, applications of 275Ч277 387Ч388 404Ч408 423Ч424 470Ч474
Asymptotic expansions of integrals, methods for, steepest descents, method of 264Ч270
Asymptotic expansions of integrals, methods for, steepest descents, method of, applications of 323Ч328 550Ч551
Asymptotic expansions of integrals, methods for, Van der Waerden's method 270
Asymptotic expansions of integrals, methods for, Van der Waerden's, application of 270
Asymptotic expansions of integrals, methods for, Watson's lemma 257
Asymptotic expansions of integrals, methods for, Watson's lemma, applications of 260 326 327Ч328
Asymptotic expansions, nature of 251Ч252
Asymptotic expansions, Poincare's definition of 252Ч253
Asymptotic expansions, properties of 253Ч255
Asymptotic expansions, properties of, differentiation 255
Asymptotic expansions, properties of, integration 254Ч255
Asymptotic expansions, properties of, product, quotient, sum 254
Asymptotic expansions, properties of, uniqueness 253Ч254
Axially symmetric compressional waves in circular cylindrical rod 220Ч223
Axially symmetric diffraction problems for spherical cavity 565Ч567
Axially symmetric plate problems 470Ч476
Axially symmetric torsional waves in circular cylindrical rod 217Ч220
Axially symmetric torsional waves in thin plate 290
Axially symmetric vertical point load problem, half space 333Ч348
Axially symmetric waves 68 338Ч348 470Ч476
Bar velocity 222
Bernoulli Ч Euler beam (bending theory) 6 8. approximate
Bessel functions, modified 283 523Ч525 562Ч565
Bessel functions, modified, asymptotic expansions of 283
Bessel functions, modified, Hankel function relation 287
Bessel functions, ordinary, asymptotic expansion of 469
Bilateral Laplace transform 241Ч242
Bilateral Laplace transform in cylindrical cavity diffraction problem 537Ч542
Bilateral Laplace transform, properties of 242
Body force problems 78Ч94
Body force problems, center of compression in 91Ч92
Body force problems, center of rotation in 92Ч93
Body force problems, distributed source of potentials in 83Ч84
Body force problems, distributed source of potentials in, retarded potential solutions for 84 88 94
Body force problems, double forces in 91Ч93
Body force problems, early work on 4
Body force problems, general solution for displacement in 84Ч85
Body force problems, governing inhomogeneous wave equations for 80
Body force problems, line source of potentials in 85
Body force problems, line source of potentials in, solution for 86
Body force problems, point load in 86Ч91
Body force problems, point load in, dilation solution for 90
Body force problems, point load in, displacement solution for 89
Body force problems, point load in, rotation solution for 90
Body force problems, point load in, stress solution for 90
Body force problems, point load in, wavefronts, ramp input, for 90Ч91
Body force problems, point load in, waves generated by 90
Body force problems, point source of potentials, in 83Ч84
Body force problems, point source of potentials, in, solutions for 82Ч83
Body force problems, time harmonic 93
Body waves in bounded media 68Ч69
Body waves in bounded media, cylindrical wave surfaces of 69
Body waves in bounded media, generation of interface waves by 68Ч69
Body waves in bounded media, interference of 69
Body waves in bounded media, reflection and refraction of 69
Body waves, fundamental 57Ч63
Body waves, fundamental, dilatation 58
Body waves, fundamental, dilatational displacement 58
Body waves, fundamental, equivolumnal displacement 57Ч58
Body waves, fundamental, governing equations for 57Ч63
Body waves, fundamental, propagation speeds for 57Ч58
Body waves, fundamental, rotation 58
Body waves, time harmonic 69Ч70
Body waves, time harmonic, axially symmetric 70
Body waves, time harmonic, frequency of 69
Body waves, time harmonic, Helmholtz equations for 69
Body waves, time harmonic, nodal points of 70
Body waves, time harmonic, standing 70
Body waves, time harmonic, trains of 70
Body waves, time harmonic, wave number of 69
Body waves, time harmonic, wavelength of 69
Body waves, types of 63Ч68
Body waves, types of, axially symmetric 68
Body waves, types of, nonaxially symmetric 68
Body waves, types of, plane 63Ч67
Body waves, types of, spherically symmetric 67
Boundary-initial value problems fundamental 46Ч47
Boundary-initial value problems fundamental, integral representations in 94Ч96
Boundary-initial value problems fundamental, integral representations in Kirchhoff's formula 95
Boundary-initial value problems fundamental, integral representations in Love's formula 95Ч96
Boundary-initial value problems fundamental, integral transform methods in see Integral transform methods
Boundary-initial value problems fundamental, method of characteristics in 112Ч115
Boundary-initial value problems fundamental, uniqueness of solutions of 3 47 50Ч51
Boundary-initial value problems fundamental, uniqueness of solutions of, discontinuous loadings 52
Boundary-initial value problems fundamental, uniqueness of solutions of, finite body 47 50Ч51
Boundary-initial value problems fundamental, uniqueness of solutions of, infinite anisotropic body 51
Boundary-initial value problems fundamental, uniqueness of solutions of, infinite body 51
Boundedness condition, solution, algebraic 452 461
Boundedness condition, solution, algebraic, approximation corresponding to long time 454Ч455 462
Boundedness condition, solution, for semiinfinite plate with nonmixed edge conditions 446Ч448 461Ч462
Boundedness condition, solution, integral equations representing 448
Branches of frequency equations for, plate, approximations 369 381 475
Branches of frequency equations for, plate, infinite 7. See also Rayleigh Ч Lamb frequency equation
Branches of frequency equations for, rod, approximations 7Ч8 219 368Ч369 381
Branches of frequency equations for, rod, infinite circular cylindrical 7. See also Pochhammer frequency equations
Bromwich contour 236
Bulk modulus (Modulus of compression) 41
Buried line dilatational source in half space 329Ч332
Cagniard Ч deHoop method in half plane diffraction problem 490 492Ч496 498Ч499 504Ч516
Cagniard Ч deHoop method, for nonaxymmetric, surface normal point traveling load problem 351Ч360
| Cagniard Ч deHoop method, for nonaxymmetric, surface normal point traveling load problem, displacements in 357Ч360
Cagniard Ч deHoop method, for nonaxymmetric, surface normal point traveling load problem, integral equations for 356 358 359
Cagniard Ч deHoop method, for nonaxymmetric, surface normal point traveling load problem, integration paths in, deformed 353 357Ч358
Cagniard Ч deHoop method, for nonaxymmetric, surface normal point traveling load problem, Laplace transformed 355Ч356 359
Cagniard Ч deHoop method, for nonaxymmetric, surface normal point traveling load problem, principal value integrals in 359
Cagniard Ч deHoop method, for nonaxymmetric, surface normal point traveling load problem, singularities and controur integrations in 352Ч355 357Ч359
Cagniard Ч deHoop method, for nonaxymmetric, surface normal point traveling load problem, transformations in, basic 351 352 357 358Ч359
Cagniard Ч deHoop method, for nonaxymmetric, surface normal point traveling load problem, wavefront approximations in 361
Cagniard Ч deHoop method, for plane-strain problems 302Ч319 329Ч332
Cagniard Ч deHoop method, for plane-strain problems, displacements in 312Ч314
Cagniard Ч deHoop method, for plane-strain problems, integral equations for 310 312
Cagniard Ч deHoop method, for plane-strain problems, integration paths in, deformed 303Ч306 307Ч308 311
Cagniard Ч deHoop method, for plane-strain problems, Laplace transformed 307 309 310 311Ч312
Cagniard Ч deHoop method, for plane-strain problems, principal value integrals in 311
Cagniard Ч deHoop method, for plane-strain problems, singularities, contour integration in 303Ч306
Cagniard Ч deHoop method, for plane-strain problems, transformations in, basic 302 303
Cagniard Ч deHoop method, for plane-strain problems, wavefront approximations in 319Ч323
Cagniard's method, early use of 5
Calculus of variations, use of 369Ч373
Carrier wave 187
Carrier wave, modulation of 187
Carrier wave, modulation of, frequency of 187
Carrier wave, of simple wave group 187
Cauchy problems See Initial value problem
Cauchy Ч Goursat theorem, use of 259 286
Caustic 557 559
Caustic, singular stress at 558. See also Focusing wave
Cavity source problems 277Ч290
Cavity source problems, boundary-initial value problem 278
Cavity source problems, boundary-initial value problem, displacement-potential relation 279
Cavity source problems, boundary-initial value problem, Laplace transform solution method 278Ч281
Cavity source problems, boundary-initial value problem, solution 281
Cavity source problems, boundary-initial value problem, solution, response of stresses in 282
Cavity source problems, boundary-initial value problem, solution, static 281
Cavity source problems, boundary-initial value problem, solution, verification of 181
Cavity source problems, boundary-initial value problem, solution, wavefronts of 281
Cavity source problems, boundary-initial value problem, stress-potential relation 279
Cavity source problems, circular cylindrical cavity in plate, Kromm's solution method 290
Cavity source problems, circular cylindrical cavity in plate, uniform pressure on 282Ч290
Cavity source problems, circular cylindrical cavity in plate, uniform shear stress, rotary velocity on 290
Cavity source problems, circular cylindrical cavity, decaying uniform pressure on 290
Cavity source problems, circular cylindrical cavity, uniform, boundary-initial value problem 283
Cavity source problems, circular cylindrical cavity, uniform, displacement-potential relation 284
Cavity source problems, circular cylindrical cavity, uniform, Laplace transform solution method 283Ч287
Cavity source problems, circular cylindrical cavity, uniform, Laplace transform solution method, singularities, contour integration in 284Ч287
Cavity source problems, circular cylindrical cavity, uniform, pressure in 282Ч290
Cavity source problems, circular cylindrical cavity, uniform, solution 286Ч287
Cavity source problems, circular cylindrical cavity, uniform, solution by method of characteristics 290
Cavity source problems, circular cylindrical cavity, uniform, solution, static 289
Cavity source problems, circular cylindrical cavity, uniform, solution, stress responses in 287
Cavity source problems, circular cylindrical cavity, uniform, solution, verification of 288
Cavity source problems, circular cylindrical cavity, uniform, solution, wavefronts in 289Ч290
Cavity source problems, circular cylindrical cavity, uniform, stress-potential relations 284
Cavity source problems, spherical cavity, nonsymmetric sources 282
Cavity source problems, spherical cavity, uniform pressure on 277Ч282
Center of compression 91
Center of rotation 92
Characteristic length 1
Characteristics 75
Characteristics, method of 107Ч115
Characteristics, method of, for one-dimensional problems 107Ч115
Characteristics, method of, for one-dimensional problems, boundary-initial value problems, numerical method 112Ч115
Characteristics, method of, for one-dimensional problems, characteristic condition in 109
Characteristics, method of, for one-dimensional problems, characteristic directions in 109
Characteristics, method of, for one-dimensional problems, first hyperbolic theorem, initial values, numerical method 110Ч112
Characteristics, method of, for one-dimensional problems, second hyperbolic theorem, initial values, numerical method 112
Characteristics, method of, for one-dimensional problems, uniqueness of solution 112
Characteristics, method of, for one-dimensional problems, use of 290
Characteristics, method of, for two-dimensional problems 115
Characteristics, theory of 17. See also Wavefronts; propagating
Coefficients of reflection 123
Coefficients of transmission 160
Completeness of Lame solution 3 61Ч62 116
Composite materials, waves in, monographs on 577
Compressional waves in a thin circular cylindrical rod, approximate theories for 367Ч369 371Ч374 392Ч393
Compressional waves in a thin circular cylindrical rod, longitudinal impact, generated by 388Ч389 393
Compressional waves in a thin plate with circular cylindrical cavity, cavity wall pressure, generated by 287
Compressional waves in an infinite plate with circular cylindrical cavity, cavity wall normal displacement, generated by 474
Compressional waves in an infinite semi-infinite circular cylindrical rod, end load, generated by 466
Compressional waves in an infinite semi-infinite circular cylindrical rod, frequency equations for 221
Compressional waves in an infinite semi-infinite circular cylindrical rod, frequency spectra for 208Ч209 222
Compressional waves in an infinite semi-infinite circular cylindrical rod, motion generated by 222Ч223
Compressional waves in an infinite semi-infinite circular cylindrical rod, potential modes for 221
Compressional waves in an infinite semi-infinite circular cylindrical rod, shock tube excitation of 390Ч393 437
Compressional waves in an infinite solid generated by cavity pressure sources, circular cylindrical 287
Compressional waves in an infinite solid generated by cavity pressure sources, spherical 282
Compressional waves in an infinite, semi-infinite plate, cylindrical dilatational, equivolumnal wave surfaces in 179Ч180 210
Compressional waves in an infinite, semi-infinite plate, frequency equations for 183 197
Compressional waves in an infinite, semi-infinite plate, frequency equations for, branches of 197Ч201
Compressional waves in an infinite, semi-infinite plate, frequency spectra for 185 198 202
Compressional waves in an infinite, semi-infinite plate, longitudinal impact, generated by 436Ч437
Compressional waves in an infinite, semi-infinite plate, mixed edge pressure, generated by 436Ч437
Compressional waves in an infinite, semi-infinite plate, near base normal line loads, cantilever, generated by 465
Compressional waves in an infinite, semi-infinite plate, nonmixed edge line load, generated by 463Ч465
Compressional waves in an infinite, semi-infinite plate, nonmixed edge pressure, generated by 455Ч457
Compressional waves in an infinite, semi-infinite plate, nonmixed edge velocities, generated by 465Ч466
Compressional waves in an infinite, semi-infinite plate, normal line loads, generated by 420Ч422
Compressional waves in an infinite, semi-infinite plate, normal point loads, generated by 470Ч472
Compressional waves in an infinite, semi-infinite plate, P, SV waves in 178Ч180
Compressional waves in an infinite, semi-infinite plate, phase velocity spectra for 185
Compressional waves in an infinite, semi-infinite plate, thermal field, generated by 475Ч477
Compressional waves in an infinite, semi-infinite plate, thickness modes in 185
Conical flows, Buseman's method of 517. See also Self-similar solutions
Conical, waves 358 360Ч361
Convolution theorem of exponential Fourier tranform 245
Convolution theorem of Laplace transform 239
Convolution theorem, use of 313 541Ч542
Coordinates, cylindrical 68
Coordinates, rectangular Cartesian 19 42
Coordinates, spherical 67
Cusp-type wavefronts in anisotropic plates 443
Cutoff frequencies for plate, with mixed face conditions 188
Cutoff frequencies for plate, with mixed face conditions, group velocities at 189
Cutoff frequencies for plate, with mixed face conditions, P, SV waves at 189
Cutoff frequencies for plate, with mixed face conditions, phase velocities at 189
Cutoff frequencies for plate, with traction free faces 203Ч204
Cutoff waves, influence of in transient response of a plate 420 475Ч477
Cylindrical shell, circular, time harmonic waves in 226
Cylindrical waves, circular 68 70 77Ч78 286Ч289
Cylindrical waves, in diffraction 485Ч487 494Ч495 515Ч517
Cylindrical waves, in half space 314 316 319 331Ч332
Cylindrical waves, in plates 69 180Ч186 188Ч214 420Ч422 440Ч443 456Ч457 464Ч465
D'Alembert's principle 43 375
D'Alembert's solution for one-dimensional initial value problem 63Ч64
Deformation 30Ч38
Deformation and motion, description of Eulerian (spatial) 19
Deformation and motion, description of Lagrangian (material) 19Ч20
Deformation, finite 31
Deformation, infinitesimal 32
Deformation, pure 34 35Ч36
Delta functions, Dirac 80Ч82 240
Delta functions, Dirac, derivatives of 81
Delta functions, Dirac, for cartesian coordinates 81
Delta functions, Dirac, for spherical coordinates 81Ч82
Delta functions, Dirac, Laplace transform of 241
Delta functions, Dirac, symmetrical 300
Diffraction problems, elastic pulse by circular cylindrical obstacle 517Ч560
Diffraction problems, elastic pulse by circular cylindrical obstacle, Friedlander's representation of solution 520Ч521
Diffraction problems, elastic pulse by circular cylindrical obstacle, Friedlander's representation of solution, Poisson's summation formula 520Ч521
Diffraction problems, elastic pulse by circular cylindrical obstacle, Friedlander's representation of solution, Riemann surface in 0; interpreted as 521
Diffraction problems, elastic pulse by circular cylindrical obstacle, Friedlander's representation of solution, wave sum in 521
Diffraction problems, elastic pulse by circular cylindrical obstacle, Friedlander's representation of solution, waveform of function in 521
Diffraction problems, elastic pulse by circular cylindrical obstacle, line source by circular cylindrical cavity 518Ч536
Diffraction problems, elastic pulse by circular cylindrical obstacle, line source by circular cylindrical cavity, diffracted wavefront, ray 518Ч519
Diffraction problems, elastic pulse by circular cylindrical obstacle, line source by circular cylindrical cavity, illuminated zone 518Ч519
Diffraction problems, elastic pulse by circular cylindrical obstacle, line source by circular cylindrical cavity, incident wavefront, ray 518
Diffraction problems, elastic pulse by circular cylindrical obstacle, line source by circular cylindrical cavity, limiting cases of 519Ч520
Diffraction problems, elastic pulse by circular cylindrical obstacle, line source by circular cylindrical cavity, reflected wavefront, ray 518
Diffraction problems, elastic pulse by circular cylindrical obstacle, line source by circular cylindrical cavity, shadow zone 518
Diffraction problems, elastic pulse by circular cylindrical obstacle, line source by circular cylindrical cavity, source of diffracted wavefront 519
|
|
 |
| –еклама |
 |
|
|
 |
 |
|
 |
|
ќ проекте
|
|
ќ проекте



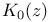 function, integral representation for
function, integral representation for