|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Rencher A.C. Ч Methods of multivariate analysis |
|
|
 |
| ѕредметный указатель |
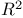 (squared multiple correlation) 332Ч333 337 349 355 361Ч362 365 375Ч376 422Ч423 (squared multiple correlation) 332Ч333 337 349 355 361Ч362 365 375Ч376 422Ч423
 -statistic: additional information, test for 136Ч139 -statistic: additional information, test for 136Ч139
 -statistic: and F-distribution 119 124 137Ч138 -statistic: and F-distribution 119 124 137Ч138
 -statistic: and profile analysis 139Ч148 -statistic: and profile analysis 139Ч148
 -statistic: and profile analysis, one sample 139Ч141 -statistic: and profile analysis, one sample 139Ч141
 -statistic: and profile analysis, two samples 141Ч148 -statistic: and profile analysis, two samples 141Ч148
 -statistic: assumptions for 122 -statistic: assumptions for 122
 -statistic: characteristic form 118 123 -statistic: characteristic form 118 123
 -statistic: chi-square approximation for 120 -statistic: chi-square approximation for 120
 -statistic: computation of 130Ч132 -statistic: computation of 130Ч132
 -statistic: computation of, by MANOVA 130 -statistic: computation of, by MANOVA 130
 -statistic: computation of, y regression 130Ч132 -statistic: computation of, y regression 130Ч132
 -statistic: for a subvector 136Ч139 -statistic: for a subvector 136Ч139
 -statistic: full and reduced model test 137 -statistic: full and reduced model test 137
 -statistic: likelihood ratio test 126 -statistic: likelihood ratio test 126
 -statistic: matched pairs 134Ч136 -statistic: matched pairs 134Ч136
 -statistic: one-sample 117Ч121 -statistic: one-sample 117Ч121
 -statistic: paired observations 134Ч136 -statistic: paired observations 134Ч136
 -statistic: properties of 119Ч120 123Ч124 -statistic: properties of 119Ч120 123Ч124
 -statistic: table of critical values for -statistic: table of critical values for  558Ч561 558Ч561
 -statistic: two-sample 122Ч126 -statistic: two-sample 122Ч126
Additional information, test for 136Ч139 231Ч233
Air pollution data 502
Airline distance data 508
Algebra, matrix see Matrix algebra
Analysis of variance: multivariate (MANOVA): additional information, test for 231Ч233
Analysis of variance: multivariate (MANOVA): and canonical correlation 376Ч377
Analysis of variance: multivariate (MANOVA): association, measures of 173Ч176
Analysis of variance: multivariate (MANOVA): assumptions, checking on 198Ч199
Analysis of variance: multivariate (MANOVA): contrasts 180Ч183
Analysis of variance: multivariate (MANOVA): discriminant function 165 184Ч185 191
Analysis of variance: multivariate (MANOVA): growth curves 221Ч230. See also Growth curves; Repeated measures designs
Analysis of variance: multivariate (MANOVA): H and E matrices 160Ч161
Analysis of variance: multivariate (MANOVA): higher order models 195Ч196
Analysis of variance: multivariate (MANOVA): individual variables, discriminant function 184Ч185 191
Analysis of variance: multivariate (MANOVA): individual variables, experimentwise error rate 183Ч185
Analysis of variance: multivariate (MANOVA): individual variables, protected tests 184
Analysis of variance: multivariate (MANOVA): individual variables, tests on 163Ч164 183Ч186
Analysis of variance: multivariate (MANOVA): Lawley Ч Hotelling test 167
Analysis of variance: multivariate (MANOVA): Lawley Ч Hotelling test, table of critical values 524Ч528
Analysis of variance: multivariate (MANOVA): likelihood ratio test 164
Analysis of variance: multivariate (MANOVA): mixed models 196Ч198
Analysis of variance: multivariate (MANOVA): mixed models, expected mean squares 196Ч197
Analysis of variance: multivariate (MANOVA): multivariate association, measures of 173Ч176
Analysis of variance: multivariate (MANOVA): one-way 158Ч161
Analysis of variance: multivariate (MANOVA): one-way contrasts 180Ч183
Analysis of variance: multivariate (MANOVA): one-way contrasts, orthogonal 181
Analysis of variance: multivariate (MANOVA): one-way model 159
Analysis of variance: multivariate (MANOVA): one-way, unbalanced 168
Analysis of variance: multivariate (MANOVA): Pillai's test 166
Analysis of variance: multivariate (MANOVA): profile analysis 199Ч201
Analysis of variance: multivariate (MANOVA): repeated measures 204Ч221. See also Repeated measures designs; Growth curves
Analysis of variance: multivariate (MANOVA): Roy's test (union-intersection) 164Ч166
Analysis of variance: multivariate (MANOVA): Roy's test (union-intersection), table of critical values 517Ч520
Analysis of variance: multivariate (MANOVA): stepwise discriminant analysis 233
Analysis of variance: multivariate (MANOVA): stepwise selection of variables 233
Analysis of variance: multivariate (MANOVA): test for additional information 231Ч233
Analysis of variance: multivariate (MANOVA): test on a subvector 231Ч233
Analysis of variance: multivariate (MANOVA): test statistics 161Ч173
Analysis of variance: multivariate (MANOVA): test statistics and  169 169
Analysis of variance: multivariate (MANOVA): test statistics eigenvalues 168
Analysis of variance: multivariate (MANOVA): test statistics, comparison of 169Ч170 176Ч178
Analysis of variance: multivariate (MANOVA): test statistics, power of 176Ч178
Analysis of variance: multivariate (MANOVA): tests on individual variables 163Ч174 183Ч186 191
Analysis of variance: multivariate (MANOVA): tests on individual variables, discriminant function 165 184Ч185 191
Analysis of variance: multivariate (MANOVA): tests on individual variables, experimentwise error rate 183Ч185
Analysis of variance: multivariate (MANOVA): tests on individual variables, protected tests 184
Analysis of variance: multivariate (MANOVA): two-way 188Ч195
Analysis of variance: multivariate (MANOVA): two-way contrasts 190Ч191
Analysis of variance: multivariate (MANOVA): two-way discriminant function 191
Analysis of variance: multivariate (MANOVA): two-way interactions 189Ч190
Analysis of variance: multivariate (MANOVA): two-way main effects 189Ч190
Analysis of variance: multivariate (MANOVA): two-way model 189
Analysis of variance: multivariate (MANOVA): two-way test statistics 190
Analysis of variance: multivariate (MANOVA): two-way tests on individual variables 191
Analysis of variance: multivariate (MANOVA): unbalanced one-way 168
Analysis of variance: multivariate (MANOVA): union-intersection test 164
Analysis of variance: multivariate (MANOVA): Wilks'  (likelihood ratio) test 161Ч164 (likelihood ratio) test 161Ч164
Analysis of variance: multivariate (MANOVA): Wilks'  (likelihood ratio) test, chi-square approximation 162 (likelihood ratio) test, chi-square approximation 162
Analysis of variance: multivariate (MANOVA): Wilks'  (likelihood ratio) test, F approximation 162 (likelihood ratio) test, F approximation 162
Analysis of variance: multivariate (MANOVA): Wilks'  (likelihood ratio) test, partial (likelihood ratio) test, partial  -statistic 232 -statistic 232
Analysis of variance: multivariate (MANOVA): Wilks'  (likelihood ratio) test, properties of 162Ч164 (likelihood ratio) test, properties of 162Ч164
Analysis of variance: multivariate (MANOVA): Wilks'  (likelihood ratio) test, table of critical values 501Ч516 (likelihood ratio) test, table of critical values 501Ч516
Analysis of variance: multivariate (MANOVA): Wilks'  (likelihood ratio) test, transformations to exact F 162Ч163 (likelihood ratio) test, transformations to exact F 162Ч163
Analysis of variance: univariate (ANOVA): one-way 156Ч158
Analysis of variance: univariate (ANOVA): one-way contrasts 178Ч180
Analysis of variance: univariate (ANOVA): one-way contrasts, orthogonal 179Ч180
Analysis of variance: univariate (ANOVA): one-way SSH, SSE, F-statistic 158
Analysis of variance: univariate (ANOVA): two-way 186Ч188
Analysis of variance: univariate (ANOVA): two-way contrasts 188
Analysis of variance: univariate (ANOVA): two-way F-test 188
Analysis of variance: univariate (ANOVA): two-way interaction 187
Analysis of variance: univariate (ANOVA): two-way main effects 187Ч188
Analysis of variance: univariate (ANOVA): two-way model 186
anova see Analysis of variance univariate
Association, measures of 173Ч176 349Ч351
Athletic record data 480
Bar steel data 192
Beetles data 150
Bilinear form 19Ч20
Biplots 531Ч539
Biplots, coordinates of points 533Ч534
Biplots, coordinates of points, correlation 534
Biplots, coordinates of points, cosine 534 537
Biplots, points for observations 531Ч534
Biplots, points for variables 531Ч534
Biplots, principal component approach 531Ч532 535
Biplots, singular value decomposition 532Ч533 535
Birth and death data 543
Bivariate normal distribution 46 84 88Ч89 133
Blood data 237
Blood pressure data 245
Bonferroni critical values 127
Bonferroni critical values, table 562Ч565
Box's M-test 257Ч259
Box's M-test, table of exact critical values 588Ч589
Bronchus data 154
Burt matrix 526Ч529
Byssinosis data 545Ч546
Calcium dat 56
Calculator speed data 210
Canonical correlation(s) 174 260 361Ч378
Canonical correlation(s) and discriminant analysis 376Ч378
Canonical correlation(s) and eigenvalues 362Ч363 377Ч378
Canonical correlation(s) and MANOVA 376Ч378
Canonical correlation(s) and MANOVA, dummy variables 376Ч377
Canonical correlation(s) and measures of association 362 373Ч374
Canonical correlation(s) and multiple correlation 361Ч362 366 376
Canonical correlation(s) and regression 368Ч369 374Ч376
Canonical correlation(s) with grouping variables 174
Canonical correlation(s) with test for independence of two subvectors 260 367Ч368
Canonical correlation(s), canonical variates see Canonical variates
Canonical correlation(s), definition of 362Ч364
Canonical correlation(s), properties of 366Ч367
Canonical correlation(s), redundancy analysis 373Ч374
Canonical correlation(s), subset selection 376
Canonical correlation(s), tests of significance 367Ч371
Canonical correlation(s), tests of significance, all canonical correlations 367Ч369
Canonical correlation(s), tests of significance, all canonical correlations and test of independence 367Ч368
Canonical correlation(s), tests of significance, all canonical correlations and test of overall regression 367Ч368 375
Canonical correlation(s), tests of significance, all canonical correlations, comparison of tests 368Ч369
Canonical correlation(s), tests of significance, subset of canonical correlations 369Ч371
Canonical correlation(s), tests of significance, subset selection 376
Canonical correlation(s), tests of significance, test of a subset in regression 375Ч376
Canonical variates: and regression 374Ч376
Canonical variates: correlations among 364
Canonical variates: definition of 363
Canonical variates: interpretation 371Ч374
Canonical variates: interpretation by correlations (structure coefficients) 373
Canonical variates: interpretation by rotation 373
| Canonical variates: interpretation by standardized coefficients 371Ч373
Canonical variates: redundancy analysis 373Ч374
Canonical variates: standardized coefficients 365 371Ч373
categorical variables see Dummy variables
Central Limit Theorem (Multivariate) 91
Characteristic form: of  -statistic 118 123 -statistic 118 123
Characteristic form: of t-statistic 117 122
Characteristic roots see Eigenvalues
Chemical data 340
Chi-square distribution 86 91Ч92 114
Cholesky decomposition 25Ч26
City crime data 456
Classification analysis (allocation) 299Ч321
Classification analysis (allocation), assigning a sampling unit to a group 299
Classification analysis (allocation), asymptotic optimality 302
Classification analysis (allocation), correct classification rates 307Ч309
Classification analysis (allocation), error rates 307Ч313. See also Error rates
Classification analysis (allocation), error rates as a stopping rule 311Ч313
Classification analysis (allocation), error rates, estimates of 307Ч313
Classification analysis (allocation), k-nearest neighbor rule 318Ч319
Classification analysis (allocation), nonparametric classification procedures 302 314Ч320
Classification analysis (allocation), nonparametric classification procedures, density estimators (kernel) 315Ч317
Classification analysis (allocation), nonparametric classification procedures, multinomial data (categorical variables) 314Ч315
Classification analysis (allocation), nonparametric classification procedures, multinomial data (categorical variables), dummy variables 315
Classification analysis (allocation), nonparametric classification procedures, nearest neighbor rule 318Ч320
Classification analysis (allocation), nonparametric classification procedures, nearest neighbor rule, k-nearest neighbor rule 318Ч319
Classification analysis (allocation), several groups 304Ч307
Classification analysis (allocation), several groups, linear classification functions 304Ч306
Classification analysis (allocation), several groups, linear classification functions, equal covariance matrices 304Ч305
Classification analysis (allocation), several groups, optimal classification rule (Welch) 305
Classification analysis (allocation), several groups, prior probabilities 305Ч307
Classification analysis (allocation), several groups, quadratic classification functions 306Ч307
Classification analysis (allocation), several groups, quadratic classification functions, unequal covariance matrices 306
Classification analysis (allocation), subset selection 311Ч313
Classification analysis (allocation), subset selection, stepwise discriminant analysis 311Ч313
Classification analysis (allocation), subset selection, stepwise discriminant analysis, error rate as a stopping rule 311Ч313
Classification analysis (allocation), two groups 300Ч303
Classification analysis (allocation), two groups, Fisher's classification function 300Ч302
Classification analysis (allocation), two groups, linear classification function 301Ч302
Classification analysis (allocation), two groups, optimal classification rule (Welch) 302
Classification analysis (allocation), two groups, prior probabilities 302
Cluster analysis 451Ч503
Cluster analysis and classification 451
Cluster analysis, average linkage method 463
Cluster analysis, centroid method 463Ч465
Cluster analysis, choosing the number of clusters 494Ч496
Cluster analysis, clustering observations 451Ч496
Cluster analysis, clustering variables 451 497Ч499
Cluster analysis, comparison of methods 478Ч479
Cluster analysis, complete linkage method 459Ч462
Cluster analysis, definition 451
Cluster analysis, dendrogram 456
Cluster analysis, dendrogram, crossover 471
Cluster analysis, dendrogram, examples of 458Ч459 461Ч462 464Ч465 467 469 472Ч473 476Ч477
Cluster analysis, dendrogram, inversion 471
Cluster analysis, dendrogram, reversal 471
Cluster analysis, dissimilarity 452
Cluster analysis, distance 451Ч454
Cluster analysis, distance, distance matrix 453
Cluster analysis, distance, Euclidean distance 452
Cluster analysis, distance, Minkowski metric 453
Cluster analysis, distance, profile of observation vector: level 454
Cluster analysis, distance, profile of observation vector: shape 454
Cluster analysis, distance, profile of observation vector: variation 454
Cluster analysis, distance, scale of measurement 453Ч454
Cluster analysis, distance, statistical distance 452Ч453
Cluster analysis, farthest neighbor method see Complete linkage method
Cluster analysis, flexible beta method 468Ч471
Cluster analysis, hierarchical clustering 452 455Ч481
Cluster analysis, hierarchical clustering, agglomerative method 455Ч479
Cluster analysis, hierarchical clustering, agglomerative method, average linkage 463
Cluster analysis, hierarchical clustering, agglomerative method, centroid 463Ч465
Cluster analysis, hierarchical clustering, agglomerative method, centroid, mean vectors 463
Cluster analysis, hierarchical clustering, agglomerative method, complete linkage 459Ч462
Cluster analysis, hierarchical clustering, agglomerative method, flexible beta 468Ч471
Cluster analysis, hierarchical clustering, agglomerative method, median 466
Cluster analysis, hierarchical clustering, agglomerative method, single linkage 456Ч459
Cluster analysis, hierarchical clustering, agglomerative method, Ward's method 466Ч468
Cluster analysis, hierarchical clustering, comparison of methods 478Ч479
Cluster analysis, hierarchical clustering, dendrogram 456
Cluster analysis, hierarchical clustering, divisive method 455 479Ч481
Cluster analysis, hierarchical clustering, divisive method, monothetic 479
Cluster analysis, hierarchical clustering, divisive method, polythetic 479Ч480
Cluster analysis, hierarchical clustering, properties 471Ц479
Cluster analysis, hierarchical clustering, properties, chaining 474
Cluster analysis, hierarchical clustering, properties, contraction 474
Cluster analysis, hierarchical clustering, properties, dilation 474
Cluster analysis, hierarchical clustering, properties, monotonicity 471
Cluster analysis, hierarchical clustering, properties, outliers 478Ч479
Cluster analysis, hierarchical clustering, properties, space contracting 474
Cluster analysis, hierarchical clustering, properties, space dilating 474
Cluster analysis, hierarchical clustering, properties, ultrametric 471
Cluster analysis, incremental sum of squares method see Ward's method
Cluster analysis, median method 466
Cluster analysis, nearest neighbor method see Single linkage method
Cluster analysis, nonhierarchical methods 481Ч494
Cluster analysis, nonhierarchical methods, density estimation 493
Cluster analysis, nonhierarchical methods, density estimation, dense point 493
Cluster analysis, nonhierarchical methods, density estimation, modes 493
Cluster analysis, nonhierarchical methods, mixtures of distributions 490Ч492
Cluster analysis, nonhierarchical methods, partitioning 481Ч490
Cluster analysis, nonhierarchical methods, partitioning, k-means 482Ч488
Cluster analysis, nonhierarchical methods, partitioning, k-means, seeds 482Ч487
Cluster analysis, nonhierarchical methods, partitioning, methods based on E and H 488Ч490
Cluster analysis, number of clusters: choosing the number of clusters 494Ч496
Cluster analysis, number of clusters: choosing the number of clusters, cutting the dendrogram 494Ц495
Cluster analysis, number of clusters: choosing the number of clusters, methods based on E and H 495Ч496
Cluster analysis, number of clusters: total possible number 455
Cluster analysis, optimization methods see Nonhierarchical methods partitioning
Cluster analysis, partitioning 452 481Ч490
Cluster analysis, plotting of clusters: discriminant functions 486Ч488 494
Cluster analysis, plotting of clusters: principal components 451 484
Cluster analysis, plotting of clusters: projection pursuit 451
Cluster analysis, profile of observation vector: level 454
Cluster analysis, profile of observation vector: shape 454
Cluster analysis, profile of observation vector: variation 454
Cluster analysis, similarity 451Ч455
Cluster analysis, single linkage method 456Ч459
Cluster analysis, tree diagram see dendrogram
Cluster analysis, validity of a cluster solution 496
Cluster analysis, validity of a cluster solution, cross validation 496
Cluster analysis, validity of a cluster solution, hypothesis test 496
Cluster analysis, variables and factor analysis 498
Cluster analysis, variables, clustering of 451 497Ч499
Cluster analysis, variables, correlations 497
Cluster analysis, Ward's method 466Ч468
Coated pipe data 135
Coefficient of determination see 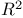
Commensurate variables see Variables commensurate
Communality see Factor analysis
Confidence interval (reference) 119 127
Contingency table: graphical analysis of see Correspondence analysis
Contingency table: higher-way table 526 528Ч529
Contingency table: two-way table 514Ч516 519 521
Contour plots 84Ч85
Contrast(s): contrast matrices in growth curves 222Ч225 227Ч230
Contrast(s): contrast matrices in repeated measures 206 208Ч221
Contrast(s): one-sample profile analysis 141Ч142
Contrast(s): one-way ANOVA 178Ч180
Contrast(s): one-way MANOVA 180Ч183
Contrast(s): orthonormal 206
Contrast(s): two-way ANOVA 188
Contrast(s): two-way MANOVA 190Ч191
Cork data 239
Correct classification rate 307Ч309
Correlation matrix: and covariance matrix 61
Correlation matrix: factor analysis on 418Ч419
Correlation matrix: partitioned 365
Correlation matrix: population correlation matrix 61
Correlation matrix: principal components from 383Ч384 393Ч397
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



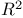 (squared multiple correlation)
(squared multiple correlation)  -statistic: additional information, test for
-statistic: additional information, test for  (likelihood ratio) test
(likelihood ratio) test