|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Кендалл М., Стюарт А. — Статистические выводы и связи |
|
|
 |
| Предметный указатель |
Линейная модель (linear model), общая линейная гипотеза 332
Линейная модель (linear model), оптимальные свойства критерия ОП 342—344
Линейная модель (linear model), смысл термина «линейная» 473—474
Линейная модель (linear model), статистика ОП в л.м. 334
Линейная модель (linear model), уточнение при одном дополнительном наблюдении, (упражнение 28.19) 497; см. «Наименьших квадратов оценки» «Регрессия»
Линейная модель (linear model), функция мощности критерия ОП 339—341
Линейная регрессия (linear regression) см. «Регрессия»
Линник Ю.В., задача о двух средних 269
Липпс (Lipps, G.F.), ранние работы о ранговой корреляции 640
Ллойд (Lloyd, E.H.), порядковые НК-оценки параметров масштаба и сдвига 126
Ллойд (Lloyd, E.H.), порядковые НК-оценки параметров масштаба и сдвига, (упражнение 19.10) 137
Логистическое распределение (logistic distribution), АОЭ критерия Вилкоксона, (упражнение 31.17) 685
Логистическое распределение (logistic distribution), МГД, (упражнение 17.5) 54
Логистическое распределение (logistic distribution), МП-оценка, (упражнение 18.29) 107
Логистическое распределение (logistic distribution), х.ф. и семиинварианты порядковых статистик, (упражнение 32.12) 714
Логнормальное распределение (lognormal distribution), МП-оценка, (упражнения 18.7—18.9, 18.19—18.20, 18.23) 101—102 104—105
Локс (Locks, M.O.), таблицы нецентрального t- распределения 342
Лоли (Lawly, D.N.), аппроксимации распределения статистики ОП 313
Лорент (Laurent, A.G.), цензурированные экспоненциальные выборки 706
Лотон (Lawton, W.H.), задача о двух средних 201
Льюис (Lewis, B.N.), таблицы с несколькими входами 777
Льюис, П. (Lewis, P.A.W.), таблицы критерия согласия 605
Льюис, Т. (Lewis, T.O.), НК-оценки в случае вырождения 124
Лэнкастер (Lancaster, H.O.), канонические корреляции и преобразование в двумерное нормальное распределение 761—762
Лэнкастер (Lancaster, H.O.), компоненты 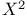 769 769
Лэнкастер (Lancaster, H.O.), компоненты 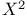 , (пример 33.13) 771—772 , (пример 33.13) 771—772
Лэнкастер (Lancaster, H.O.), компоненты 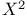 , (упражнение 33.15—33.18) 786 , (упражнение 33.15—33.18) 786
Лэнкастер (Lancaster, H.O.), полихорическое оценивание 752
Лэнкастер (Lancaster, H.O.), поправки на непрерывность при сложении значений величины 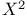 745 745
Лэнкастер (Lancaster, H.O.), таблицы с несколькими входами, (пример 33.14) 778 781
Лэнкастер (Lancaster, H.O.), таблицы с несколькими входами, (упражнение 33.8) 782—783
Лэнкастер (Lancaster, H.O.), таблицы с несколькими входами, (упражнения 33.27—33.28) 788—789
Мадански (Madansky, A.), кратчайшие доверительные интервалы 162
Мадански (Madansky, A.), таблицы с несколькими входами, (упражнения 33.24, 33.30) 788 790
Мадански (Madansky, A.), толерантные интервалы 628
Мадански (Madansky, A.), функциональные и структурные зависимости 511 528 539
Мадански (Madansky, A.), функциональные и структурные зависимости, (упражнение 29.16) 556
Майерс (Myers, M.H.), последовательные t-критерии 819
Майтра (Maitra, A.P.), достаточность 48
Мак Кей (McKay, A.T.), распределение экстремальных отклонений от среднего, (упражнение 32.21) 716—717
Мак Кендрик (McKendrick, A.G.), оценивание в цензурированных выборках, (упражнение 32.24) 717
Мак Корнак (McCornack, R.L.), таблицы критерия симметрии Вилкоксона 681
Мак Стьюарт (Mac Stewart, W.), мощность критерия знаков 690
Маккиннон (Mackinnon, W.J.), таблицы критерия знаков и доверительных интервалов для медианы 689 695
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), асимптотическая дисперсия, равная МГД 68—70
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), асимптотическая минимизация обобщенной дисперсии 85—86
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), асимптотические оптимальные свойства 62
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), в последовательных критериях, (упражнение 34.21) 831—832
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), для задач урезания и цензурирования 701—702
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), единственность при наличии достаточных статистик 59—61 80—82
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), МП-оценки для целочисленных параметров, (упражнения 18.21—18.22) 104—105
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), МП-оценки и достаточность, (пример 18.5) 59—61
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), МП-оценки и МГД-оценки 59—61
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), МП-оценки и МГД-оценки, (упражнение 18.32) 108
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), МП-оценки параметров сдвига и масштаба 93—97
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), неодинаковые исходные распределения 91—93
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), общее 58—108
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), отсутствие несмещенности, (пример 18.1) 61—62
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), отсутствие несмещенности, (пример 18.11) 82
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), поправки на группировку, (упражнения 18.24—18.25) 105—106
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), последовательные аппроксимации 75—79
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), применение для проверки согласия 570—574
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), принцип МП 58
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), семиинварианты 72—75
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), случаи неопределенности, (пример 18.4) 66—67
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), случаи неопределенности, (упражнения 18.17, 18.23, 18.33—18.35) 103—105 108
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), случай нескольких параметров 70—91
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), случай структурной и функциональной зависимости 506—511 512—518
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), совпадение с НК-оценками в нормальном случае 109 116
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), состоятельность и несостоятельность 64—67 83—84
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), состоятельность и несостоятельность, (пример 18.16) 92—93
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), состоятельность и несостоятельность, (упражнение 18.35) 108 514 516—517
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), упрощение асимптотической дисперсии и дисперсионной матрицы при наличии достаточности 71 84
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), характеризация исходных распределений, имеющих МП-оценки заданной формы, (упражнения 18.2—18.3) 100
Максимального правдоподобия (МП-)оценки (maximum likelihood (ML) estimators), эффективность и асимптотическая нормальность 67—72 83--86
Манн (Mann, H.B.), выбор классов для критерия согласия 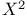 576 583—587 576 583—587
Манн (Mann, H.B.), дисперсия величины 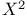 , (упражнение 30.3) 618 , (упражнение 30.3) 618
Манн (Mann, H.B.), критерий Вилкоксона 660
Манн (Mann, H.B.), критерий ранговой корреляции для тренда 647—649
Манн (Mann, H.B.), критерий ранговой корреляции для тренда, (упражнение 31.8) 684
Манн (Mann, H.B.), несмещенность критерия 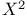 580 580
Манн (Mann, H.B.), таблицы Тэнга 340
Мантел (Mantel, N.), доверительные интервалы для нелинейных функций 175
Мариц (Maritz, J.S.), бисериальная корреляция 416
Марсалья (Marsaglia, G.), квадратичные формы от нецентральных нормальных величин 308
Марсалья (Marsaglia, G.), многомерная нормальная регрессия, (упражнение 27.21) 460
Масштабные параметры (scale parameters) см. «Сдвига и масштаба параметры»
МГД см. «Минимальная граница дисперсии»
МД см. «Минимальной дисперсии оценки»
Медиана (median), доверительные интервалы для нее 694—695
Медиана (median), доверительные интервалы для нее, (упражнение 32.4) 713
Медиана (median), критерии знаков для нее 689—692
Медиана (median), критерии знаков для нее, (упражнение 32.1) 712
Менделя данные о горохе (Mendelian pea data), (пример 30.1) 563
Менденхолл (Mendenhall, W.), цензурированные экспоненциальные выборки 705
Менденхолл (Mendenhall, W.),библиография по испытаниям на долговечность 705
Меррингтон (Merrington, M.), функции мощности критериев независимости в таблицах 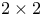 743 743
Метод моментов (method of moments) см. «Моменты»
Мешающий параметр (nuisance parameter) 279
Мешающий параметр (nuisance parameter), устранение его, (упражнение 30.18) 621
Мёрфи (Murphy R.В.), графики толерантных интервалов 697
Мизес (R. von Mises), критерий согласия 603
Микки (Mickey, M.R.), задача о двух средних 201
Микульский (Mikulskl, P.W.), эффективность ранговых критериев 672
Миллер (Miller, R.G., Jr.), оценивание с устраненным смещением 20
Миллер Л. (Miller, L.H.), таблицы критерия согласия Колмогорова 611
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)) 24—25
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), аналоги, (упражнение 17.23) 56
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), асимптотически достижимая МГД для любой функции от параметра 32
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), асимптотические улучшения в нерегулярных случаях, (упражнения 32.8—32.11) 713—714
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), МГД в конкретных задачах, (примеры 17.6—47.10) 26—27
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), МГД и достаточность 42—43
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), МГД меньшая, чем граница дисперсии, когда неизвестно несколько параметров, (упражнение 17.20) 56
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), МГД- и МД-оценки 27—28
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), МГД- и МП-оценка 59—61 68—70
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), МГД- и МП-оценка, (упражнение 18.4) 100
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), обобщение, (упражнение 18.32) 108
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), ослабление условий регулярности, (упражнения 17.21—17.22) 56
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), при последовательном выборе 819—821
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), улучшение 28—34
Минимальная граница дисперсии (МГД) (minimum variance bound (MVB)), условие достижимости 25 30
Минимальная достаточность (minimal sufficiency) см. «Достаточность»
Минимальной дисперсии (МД-)оценки (minimum variance (MV) estimators) 23—36
Минимальной дисперсии (МД-)оценки (minimum variance (MV) estimators), в классе несмещенных линейных комбинаций 115—116
Минимальной дисперсии (МД-)оценки (minimum variance (MV) estimators), единственность 34—35
Минимальной дисперсии (МД-)оценки (minimum variance (MV) estimators), единственность и полнота 254—255
Минимальной дисперсии (МД-)оценки (minimum variance (MV) estimators), МД- и МГД-оценки 27
Минимальной дисперсии (МД-)оценки (minimum variance (MV) estimators), МД- и МП-оценки 60—61
Минимальной дисперсии (МД-)оценки (minimum variance (MV) estimators), МД- и МП-оценки, (упражнение 18.13) 103
Минимальной дисперсии (МД-)оценки (minimum variance (MV) estimators), МД-оценки и достаточные статистики 44—45
Минимальной дисперсии (МД-)оценки (minimum variance (MV) estimators), МД-оценки и достаточные статистики, (упражнение 17.24) 56—57
Минимальной дисперсии (МД-)оценки (minimum variance (MV) estimators), случай урезания и цензурирования 702—703
Минимума хи-квадрат (МХК-) оценки (minimum Chi-square estimators) 132—136
Минимума хи-квадрат (МХК-) оценки (minimum Chi-square estimators), асимптотическая эквивалентность МП-оценкам, (упражнение 19.13) 138
Минимума хи-квадрат (МХК-) оценки (minimum Chi-square estimators), видоизмененные 133—134
Минимума хи-квадрат (МХК-) оценки (minimum Chi-square estimators), среднее и дисперсия, (упражнение 19.14) 138
Митра (Mitra, S.К.), гипотезы в таблицах с несколькими входами 780
Митра (Mitra, S.К.), модели для таблицы 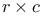 749 749
Митра (Mitra, S.К.), урезанное распределение Пуассона, (упражнение 32.20) 716
Многократные сравнения (multiple comparisons), в таблицах 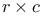 752 752
Многомерное нормальное распределение (multi-normal distribution), бисериальные методы, (упражнение 26.12) 420
Многомерное нормальное распределение (multi-normal distribution), дисперсия квадратичной формы, (упражнение 19.3) 136
Многомерное нормальное распределение (multi-normal distribution), инвариантность свойства независимости при ортогональном преобразовании 444
Многомерное нормальное распределение (multi-normal distribution), инвариантность свойства независимости при ортогональном преобразовании, (упражнение 27.7) 458
Многомерное нормальное распределение (multi-normal distribution), множественная корреляция 450—457
Многомерное нормальное распределение (multi-normal distribution), несмещенность критериев ОП о независимости 329
Многомерное нормальное распределение (multi-normal distribution), предельные значения величины 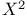 , (упражнения 33.7—33.8) 782—783 , (упражнения 33.7—33.8) 782—783
Многомерное нормальное распределение (multi-normal distribution), с матрицей внутриклассовой корреляции, (упражнения 27.17—27.18) 459
Многомерное нормальное распределение (multi-normal distribution), случаи, когда существует одномерная достаточная статистика без РНМ критерия, (пример 22.11) 240—241
Многомерное нормальное распределение (multi-normal distribution), частная корреляция и регрессия 423—430
| Многомерное нормальное распределение (multi-normal distribution), частная корреляция и регрессия, (упражнения 27.4, 27.6, 27.21) 457—458 460
Множественная корреляция (multiple correlation) 445—456
Множественная корреляция (multiple correlation), безусловное распределение в многомерном нормальном случае 450—454
Множественная корреляция (multiple correlation), безусловное распределение в многомерном нормальном случае, (упражнения 27.14—27.16) 459
Множественная корреляция (multiple correlation), геометрическая интерпретация 447
Множественная корреляция (multiple correlation), коэффициент 445—447
Множественная корреляция (multiple correlation), м.к. с некоррелированными регрессорами, (упражнение 27.20) 460
Множественная корреляция (multiple correlation), несмещенное оценивание в многомерном нормальном случае 456—457
Множественная корреляция (multiple correlation), отсеивание переменных 448—449
Множественная корреляция (multiple correlation), условное выборочное распределение в нормальном случае 449—450
Множественная корреляция (multiple correlation), условное выборочное распределение в нормальном случае, (упражнение 27.13) 458
Мозес (Moses, L.E.), критерии различия в масштабе 675
Молдон (Mauldon, J.G.), фидуциальный парадокс 212
Моменты (moments), метод моментов, эффективность 97—100
Моменты (moments), метод моментов, эффективность, (упражнения 18.9, 18.17, 18.20, 18.27—18.28) 102—104 106—107
Морэн (Moran, P.A.P.), распределение множественного коэффициента корреляции 452
Мошмэн (Moshman J.), двойная выборка 826
Мощность (power), критерия 223—225
Мощность (power),функция мощности 242; см. «Критерии для проверки гипотез»
МП см. «Максимального правдоподобия оценки»
Муд (Mood, A.M.), двухвыборочные критерии 674
Муд (Mood, A.M.), критерий для проверки случайности, основанный на медиане, (упражнение 31.12) 684
Муд (Mood, A.M.), критические значения для критерия знаков 689
Мультиномиальное распределение (multinomial distribution), критерии согласия для данных о горохе, (пример 30.1) 563
Мультиномиальное распределение (multinomial distribution), критерий однородности 788
Мультиномиальное распределение (multinomial distribution), м.р. как основа критериев согласия 559—574
Мультиномиальное распределение (multinomial distribution), МП-оценка числа классов, когда все вероятности одинаковы, (упражнение 18.10) 102
Мультиномиальное распределение (multinomial distribution), последовательная аппроксимация МП-оценки, (пример 18.10) 77—79
Мультиномиальное распределение (multinomial distribution), эффективность критериев ОП 370
Мур (Moore, A.Н.), цензурированные логнормальные выборки 707
Мур (Moore, A.Н.), цензурированные нормальные выборки 704
Мур П. (Moore, P.G.), оценивание, использующее две лучшие порядковые статистики, (упражнение 32.14) 715
МХК см. «Минимума хи-квадрат оценки»
Мэсси (Massey, F.J., Jr.), мощность критерия Колмогорова 613—616
Мэсси (Massey, F.J., Jr.), мощность критерия Колмогорова, (упражнение 30.16) 620
Мэсси (Massey, F.J., Jr.), таблицы критерия согласия Колмогорова 611
Наилучшие асимптотически нормальные (НАН) оценки (best asymptotically normal (BAN) estimators) 131—136
Наименьших квадратов (НК-) оценки (least squares (LS) estimators) 109—131
Наименьших квадратов (НК-) оценки (least squares (LS) estimators) в 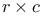 таблицах 760; см. «Линейная модель» «Регрессия» таблицах 760; см. «Линейная модель» «Регрессия»
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), (упражнения 19.1—19.8) 136—137
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), геометрическая интерпретация 116—117
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), двухэтапные, (упражнение 28.24) 498—499
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), использование дополнительной информации, (упражнения 28.17—28.18) 496—497
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), линейная модель 111—126
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), матрица рассеяния 113
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), МД-свойство 115—116
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), минимизация обобщенной дисперсии 117—118
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), несмещенность 113
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), неэффективность в пуассоновском случае, (упражнение 19.16) 138
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), НК-оценки в линейной регрессионной модели 472—493
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), общая линейная гипотеза 336
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), оценивание дисперсии ошибки 118—120
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), порядковое оценивание параметров сдвига и масштаба 126—131
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), порядковое оценивание параметров сдвига и масштаба, (упражнения 19.10—19.12) 137—138
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), приближенная линейная регрессия 382—384 434—435
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), принцип НК 109—111
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), роль предположения нормальности 120
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), случай вырождения 122—125
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), уточнение для дополнительного наблюдения, (упражнение 28.19) 497
Наименьших квадратов (НК-) оценки (least squares (LS) estimators), эквивалентность с МП-оценками в нормальном случае 109—116
Найт (Knight, W.), обратный выбор 795
НАН см. «Наилучшие асимптотически нормальные оценки»
Нарайн (Narain, R.D.), несмещенные критерии ОП для независимости 329
Независимость (independence), доказательства, использующие достаточность и полноту, (упражнение 23.6—23.10) 296
Независимость (independence), доказательства, использующие достаточность и полноту, критерии 633—647
Независимость (independence), доказательства, использующие достаточность и полноту, н. и корреляция 373—374
Независимость (independence), доказательства, использующие достаточность и полноту, н. и связь 721 сноска
Независимость (independence), доказательства, использующие достаточность и полноту, частоты 722—723
Нейман (Neyman, J.), доверительные интервалы 139 154
Нейман (Neyman, J.), достаточность и подобные области 254
Нейман (Neyman, J.), достаточность, подобные области и независимость, (упражнения 23.3—23.4) 295
Нейман (Neyman, J.), интервалы для правого конца равномерного распределения, (упражнения 20.3—20.4) 179
Нейман (Neyman, J.), критерии для проверки гипотез 219
Нейман (Neyman, J.), критерии ОП в k нормальных выборках, (упражнения 24.4—24.6) 346—347
Нейман (Neyman, J.), максимальная мощность 224
Нейман (Neyman, J.), метод ОП 301
Нейман (Neyman, J.), наиболее селективные интервалы 161—162
Нейман (Neyman, J.), НАН-оценки 131—133
Нейман (Neyman, J.), несмещенные критерии 277
Нейман (Neyman, J.), несущественные и структурные параметры 512
Нейман (Neyman, J.), НКО критериев для нормальных параметров, (пример 22.8) 237
Нейман (Neyman, J.), проверка простой гипотезы 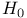 против простой против простой 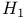 225 225
Нейман (Neyman, J.), РНМ критерии и достаточные статистики 239
Нейман (Neyman, J.), РНМ критерии и достаточные статистики, (упражнение 22.11) 248
Нейман (Neyman, J.), смещенность критерия для нормальной дисперсии, (пример 23.12) 273
Нейман (Neyman, J.), состоятельное оценивание структурной зависимости 514 534
Нейман (Neyman, J.), состоятельность критерия согласия 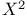 579 579
Нейман (Neyman, J.), состоятельность МП-оценок 93 514
Нейман (Neyman, J.), таблицы функции мощности (-критерия 340
Нейман (Neyman, J.), «гладкий» критерий согласия 593—596; см. «Типа A B C
Неймана — Пирсона лемма (Neyman — Pearson lemma) 225 229
Неймана — Пирсона лемма (Neyman — Pearson lemma), обобщение 280—281
Непараметрические гипотезы (non-parametric hypotheses) 220—221
Непараметрические гипотезы (non-parametric hypotheses), н.г. и свободные от распределения методы 629
Несмещенное оценивание (unbiassed estimation) 17—19
Несмещенное оценивание (unbiassed estimation) абсурдное, (упражнение 17.26) 57; см. «Смещение при оценивании»
Несмещенные критерии (unbiassed tests) 271
Несмещенные критерии (unbiassed tests), н.к. и подобные критерии 275—276
Несущественные параметры (incidental parameters) 512
Нецентральное  -распределение (non-central -распределение (non-central  -distribution) 305—310 339 -distribution) 305—310 339
Нецентральное  -распределение (non-central -распределение (non-central  -distribution) и АОЭ 368—369 -distribution) и АОЭ 368—369
Нецентральное  -распределение (non-central -распределение (non-central  -distribution), (упражнение 24.19) 350 -distribution), (упражнение 24.19) 350
Нецентральное  -распределение (non-central -распределение (non-central  -distribution), (упражнения 24.1—24.3) 345—346 -distribution), (упражнения 24.1—24.3) 345—346
Нецентральное F-распределение (non-central F-distribution) 337—341
Нецентральное t-распределение (non-central t-distribution) 341—342
Нецентральные доверительные интервалы (non-central confidence intervals) 144—145
Нётер (Noether, G.E.), АОЭ 355
Нётер (Noether, G.E.), доверительные интервалы для отношения биномиальных параметров, (упражнение 20.9) 180
Нётер (Noether, G.E.), консервативность свободных от распределения процедур в дискретных случаях 667
НК см. «Наименьших квадратов оценки»
НКО, наилучшая критическая область (BCR, best critical region) 225; см. «Критерии для проверки гипотез»
Нормальное распределение (normal distribution), АОЭ выборочной медианы, (примеры 25.2, 25.4, 25.5) 358 364 368
Нормальное распределение (normal distribution), асимптотически наиболее мощные критерии для среднего, (пример 25.1) 353
Нормальное распределение (normal distribution), байесовские интервалы 205—207
Нормальное распределение (normal distribution), в общей линейной гипотезе 333—344
Нормальное распределение (normal distribution), выбор классов для критерия 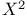 574 574
Нормальное распределение (normal distribution), границы для дисперсии при оценивании стандартного отклонения, (упражнение 17.6) 54
Нормальное распределение (normal distribution), данные о функциональной зависимости, (примеры 29.1—29.7) 518 521 529 534 540 541 543
Нормальное распределение (normal distribution), двойная выборка для среднего и дисперсии 824—826
Нормальное распределение (normal distribution), доверительные и фидуциальные интервалы для задачи о двух средних 190—205
Нормальное распределение (normal distribution), доверительные и фидуциальные интервалы для задачи о двух средних, (пример 23.10) 268—269
Нормальное распределение (normal distribution), доверительные и фидуциальные интервалы для задачи о двух средних, (пример 23.16) 288—290
Нормальное распределение (normal distribution), доверительные и фидуциальные интервалы для задачи о двух средних, (пример 24.2) 303—304
Нормальное распределение (normal distribution), доверительные и фидуциальные интервалы для задачи о двух средних, (упражнения 21.4—21.5, 21.9—21.10) 217 218
Нормальное распределение (normal distribution), доверительные интервалы для дисперсии, (пример 20.6) 156—158
Нормальное распределение (normal distribution), доверительные интервалы для дисперсии, (упражнение 20.10) 180
Нормальное распределение (normal distribution), доверительные интервалы для дисперсии, (упражнение 20.6) 179
Нормальное распределение (normal distribution), доверительные интервалы для дисперсии, (упражнение 23.18) 298
Нормальное распределение (normal distribution), доверительные интервалы для отношения двух дисперсий, (упражнение 20.7) 18
Нормальное распределение (normal distribution), доверительные интервалы для отношения двух дисперсий, (упражнение 23.18) 298
Нормальное распределение (normal distribution), доверительные интервалы для отношения двух средних, (пример 20.7) 172—174
Нормальное распределение (normal distribution), доверительные интервалы для среднего при неизвестной дисперсии 170—172
Нормальное распределение (normal distribution), доверительные интервалы для среднего, (примеры 20.1, 20.3, 20.5) 141—143 148—149 153—155
Нормальное распределение (normal distribution), доверительные области для среднего и дисперсии, (упражнение 20.5) 179
Нормальное распределение (normal distribution), доказательства свойств независимости, использующие полноту, (упражнения 23.8, 23.9) 296
Нормальное распределение (normal distribution), достаточность при оценивании среднего и дисперсии, (пример 17.17) 48
Нормальное распределение (normal distribution), использование в критериях нормальных меток 651—653
Нормальное распределение (normal distribution), использование двухвыборочного критерия 654—655 657
Нормальное распределение (normal distribution), критерии для выпадающих наблюдений 707—710
Нормальное распределение (normal distribution), критерии ОП для k выборок, (упражнения 24.4—24.6) 346—347
Нормальное распределение (normal distribution), МГД для дисперсии, (пример 17.10) 27
Нормальное распределение (normal distribution), МГД для среднего, (пример 17.6) 26
Нормальное распределение (normal distribution), минимальность и одномерная достаточность, (упражнение 23.31) 300
Нормальное распределение (normal distribution), МП-оценка общего среднего для совокупностей с разными дисперсиями, (упражнение 18.30) 107
Нормальное распределение (normal distribution), МП-оценка среднего и дисперсии, (примеры 18.11, 18.13) 82 86
Нормальное распределение (normal distribution), МП-оценка среднего, функционально связанного с дисперсией, (упражнение 18.31) 108
Нормальное распределение (normal distribution), МП-оценка стандартного отклонения, (пример 18.8) 72
Нормальное распределение (normal distribution), непригодность метода смешанных семиинвариантов для оценивания функциональной зависимости 526—529 548—549
Нормальное распределение (normal distribution), несмещенная МД-оценка квадрата среднего, (упражнение 17.7) 54
Нормальное распределение (normal distribution), несмещенная МП-оценка для среднего, (пример 18.2) 62
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



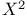
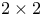
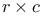
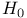 против простой
против простой 
 -распределение (non-central
-распределение (non-central