|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Кендалл М., Стюарт А, — Теория распределений |
|
|
 |
| Предметный указатель |
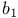 , , 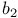 , , 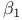 , , 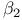 см. «Асимметрия» «Эксцесс» см. «Асимметрия» «Эксцесс»
 -распределение 510—517 -распределение 510—517
 -распределение, аппроксимации -распределение, аппроксимации  -распределения 513—517 -распределения 513—517
 -распределение, аппроксимации -распределение, аппроксимации  -распределения (упражнение 16.8) 545 -распределения (упражнение 16.8) 545
 -распределение, рекуррентные соотношения для центральных моментов (упражнение 16.3) 544 см. -распределение, рекуррентные соотношения для центральных моментов (упражнение 16.3) 544 см.
 -распределение, связь с нормальным, t и F-распределениями 528—529 -распределение, связь с нормальным, t и F-распределениями 528—529
 -распределение, таблицы 512—513 -распределение, таблицы 512—513
 -распределение, форма 511 -распределение, форма 511
 -распределение, х.ф. и моменты, сходимость к нормальному, ф.р. 511—512 -распределение, х.ф. и моменты, сходимость к нормальному, ф.р. 511—512
 -распределение, х.ф. и моменты, сходимость к нормальному, ф.р. (упражнение 16.7) 545 -распределение, х.ф. и моменты, сходимость к нормальному, ф.р. (упражнение 16.7) 545
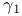 , , 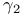 см. «Асимметрия» «Эксцесс» см. «Асимметрия» «Эксцесс»
 — величина, служащая критерием при различении типа распределений Пирсона 212 — величина, служащая критерием при различении типа распределений Пирсона 212
 — величина, служащая критерием при различении типа распределений Пирсона, бесконечность — величина, служащая критерием при различении типа распределений Пирсона, бесконечность  для III типа (упражнение 6.5) 245 для III типа (упражнение 6.5) 245
 — величина, служащая критерием при различении типа распределений Пирсона, равенство V единице для V типа (упражнение 6.6) 245 — величина, служащая критерием при различении типа распределений Пирсона, равенство V единице для V типа (упражнение 6.6) 245
(пример 4.5) 144—146
(упражнение 11.16) 377
(упражнение 5.23) 207
F-распределение см. «Дисперсионного отношения распределение»
J-образные распределения 23—27
k-статистики 385—445
k-статистики в выборках из конечной совокупности 414—419
k-статистики в терминах симметрических произведений и сумм 388—390
k-статистики как семиинварианты 385
k-статистики, двумерный случай 424—430
k-статистики, доказательство правил для нахождения выборочных семиинвариантов 430—437
k-статистики, многомерные k-статистики для оценивания нелинейных функций от семиинвариантов 418—420
k-статистики, многомерные k-статистики для оценивания нелинейных функций от семиинвариантов (упражнения 12.18—19) 423
k-статистики, определение 385
k-статистики, п.ф.м. k-статистик (упражнения 12.14—16) 422—423
k-статистики, правила для выборочных семиинвариантов в случае нормального исходного распределения (пример 12.5) 400
k-статистики, правила для нахождения выборочных семиинвариантов 390—401
k-статистики, структурные свойства 438—440
k-статистики, тензорная запись формул 440—443
k-статистики, формулы для выборочных семиинвариантов 402—411
k-статистики, формулы для выборочных семиинвариантов в нормальном случае 409—411
m-е значения см. «Экстремальные значения» «Порядковые
t-распределение см. «Стьюдента распределение»
U-образные распределения 26—27
X.ф. см. «Характеристическая функция»
Z-преобразование см. «Корреляции коэффициент»
z-распределение см. «Дисперсионного отношения распределение»
Абдель Ати (Abdel Aty S.H.), таблицы многомерных k-статистик 418
Аборт, распределение женщин по времени между зачатием и абортом (таблица 1.22) 48
Абсолютные моменты (absolute moments) 93
Абсолютные моменты (absolute moments) (упражнение 3.15) 133
Абсолютные моменты (absolute moments), неравенство Ляпунова для а.м. 93
Австралийские свадьбы, распределение а.с. (таблица 1.8) 24
Австралийские свадьбы, распределение а.с., моменты распределения а.с. (пример 3.1) 85
Австралийские свадьбы, распределение а.с., моменты распределения а.с., асимметрия и эксцесс распределения а.с. (пример 3.18) 126
Антимода (antimode) 64
Апостериорная (posterior) вероятность 276
Аппроксимация выборочных распределений (approximation to sampling distributions) 380
Аппроксимация с применением метода перевала (approximation by the method of the steepest descent) 373
Априорная (prior) вероятность 276
Асимметрические распределения (asymmetrical distributions) 23—25 см.
Асимметрия (skewness) 25
Асимметрия (skewness), выборочные моменты 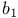 411—412 411—412
Асимметрия (skewness), выборочные моменты 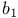 (упражнение 12.9) 421 (упражнение 12.9) 421
Асимметрия (skewness), меры а. 124—125
Асимметрия (skewness), меры а. (упражнение 3.22) 135
Асимметрия (skewness), стандартные ошибки 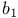 325—336 325—336
Афолт (Upholt W.M.), данные (таблица 1.5) 22
Байеса теорема (Bayes’theorem) 275
Байеса теорема (Bayes’theorem) (упражнение 4.20) 170
Байеса теорема (Bayes’theorem) (упражнения 8.1—2) 284—285
Байеса теорема (Bayes’theorem) при выборочном изучении качественных признаков (упражнение 9.3) 315
Байеса теорема (Bayes’theorem), максимальное правдоподобие 280—282
Байеса теорема (Bayes’theorem), постулат 276—282
Бартлетт (Bartlett M.S.), характеризация нормального распределения 503
Бернулли числа и полиномы (Bernoulli numbers and polynomials) 118—119
Бета-распределение (Beta distribution) первого и второго рода 210—212
Бета-распределение (Beta distribution) первого рода, арифметическое среднее (пример 2.2) 58
Бета-распределение (Beta distribution) первого рода, геометрическое и гармоническое средние (пример 2.4) 59—60
Бета-распределение (Beta distribution) первого рода, дисперсия (пример 2.8) 72
Бета-распределение (Beta distribution), полиномы Якоби при разложении в ряды 228
Бета-распределение (Beta distribution), преобразование Джонсона (упражнения 6.14—15) 247—248 см.
Бёрр (Burr I.W.), подгонка ф.р. 242—243
Бёрр (Burr I.W.), подгонка ф.р. (упражнение 6.19) 248—249
Билетов выбор или лотерея (ticket sampling) 296
Биномиальное распределение (binomial distribution), асимметрия и эксцесс (пример 3.19) 126
Биномиальное распределение (binomial distribution), асимптотическая нормальность (пример 4.6) 153—154
Биномиальное распределение (binomial distribution), в выборочном изучении качественных признаков 305—307
Биномиальное распределение (binomial distribution), в выборочном изучении качественных признаков (упражнение 9.14) 317
Биномиальное распределение (binomial distribution), двумерное 199—201
Биномиальное распределение (binomial distribution), неполные моменты (упражнения 5.2—3) 202
Биномиальное распределение (binomial distribution), общие сведения 171—178
Биномиальное распределение (binomial distribution), ошибки при нормальной аппроксимации 178
Биномиальное распределение (binomial distribution), производящая функция 45
Биномиальное распределение (binomial distribution), производящая функция моментов (характеристическая функция) (пример 3.5) 92
Биномиальное распределение (binomial distribution), производящая функция, моменты (пример 2.3) 58
Биномиальное распределение (binomial distribution), производящая функция, моменты (пример 2.9) 72
Биномиальное распределение (binomial distribution), производящая функция, моменты (пример 3.2) 86—88
Биномиальное распределение (binomial distribution), распределение среднего (пример 11.10) 360
Биномиальное распределение (binomial distribution), с отрицательным индексом см. «Отрицательное биномиальное распределение»
Биномиальное распределение (binomial distribution), смешанные биномиальные совокупности 180—182
Биномиальное распределение (binomial distribution), смешанные биномиальные совокупности (упражнение 5.6) 203
Биномиальное распределение (binomial distribution), среднее отклонение (упражнение (5.4) 202
Биномиальное распределение (binomial distribution), таблицы 177—178
Биномиальное распределение (binomial distribution), факториальные моменты (пример 3.8) 99
Биномиальное распределение (binomial distribution), факториальные моменты (упражнение 3.7) 131
Биномиальное распределение (binomial distribution), факториальные семиинварианты (пример 3.14) 111
Биномиальное распределение (binomial distribution), функция распределения 175—178
Биномиальное распределение (binomial distribution), х.ф. моменты и семиинварианты 173—175
Биномиальное распределение (binomial distribution), х.ф. моменты и семиинварианты (упражнение 5.1) 201—202
Бобы, гистограмма (рис. 1.6) 41
Бобы, подгонка распределения типа Пирсона (пример 6.1) 214—216
Бобы, подгонка с помощью логнормального распределения (пример 6.5) 237—238
Бобы, подгонка с помощью рядов Грам-Шарлье (пример 6.2) 224—225
Бобы, распределение (таблица 1.15) 40
Бозе (Bose S.S), распределение дисперсионного отношения коррелированных величин (упражнение 16.16) 546—547
Болдуин (Baldwin E.M.), таблица процентных точек г-распределения 521
Большие выборки (large samples), аппроксимации в случае б.в. см. «Стандартные ошибки»
Больших чисел закон (Law of large Numbers) 267—268
Больших чисел закон (Law of large Numbers) (упражнение 7.20) 274
Больших чисел закон (Law of large Numbers) усиленный 268
Борткевич (Bortkiewicz L.), данные о самоубийствах (таблица 1.6) 22
Браун (Brown F.A.C) см. «Эйтчисон»
Бридж, вероятности при игре в б. (пример 7.2) 254—256
Бросание костей (dice-throw), данные Уэлдона (пример 9.10) 808
Бросание костей (dice-throw), данные Уэлдона (таблица 1.14) 38
Бросание костей (dice-throw), данные Уэлдона (таблица 1.16) 45
Бросание костей (dice-throw), данные Уэлдона (таблица 5.1) 173
Букер (Booker H.S.), данные (таблица 1.21) 47
Бьенэме — Чебышева неравенство (Bienayme — Tchebycheff inequality) 128—129 149 267
Бьенэме — Чебышева неравенство (Bienayme — Tchebycheff inequality) в связи со стандартными ошибками 325
Бьенэме — Чебышева неравенство (Bienayme — Tchebycheff inequality) в случае выборочного изучения качественных признаков (упражнение 9.4) 315
Бэбингтон Смит (Babington Smith B.), данные о работе с датчиком случайных чисел (пример 9.6) 291—292
Бэбингтон Смит (Babington Smith B.), данные о телефонных номерах (таблица 1.4) 22
Бэбингтон Смит (Babington Smith B.), таблицы случайных чисел 298 304
Бэйкер (Baker G.A.), распределение суммы случайных переменных, плотность распределения каждой из которых задается в виде ряда типа А (упражнение 11.10) 375
Варианта (variate) 16
Варианта (variate), преобразования вариант 35—37 43—44
Вариация (variation), коэффициент в. 74—75
Вариация (variation), стандартная ошибка в. (пример 10.5) 324—325 326 336
Ватсо (Watson G.S.) полиномы Якоби в разложении бета-распределения 229
Вероятность (probability) 250—285
Вероятность (probability), априорная и апостериорная в. 276 см. «Правдоподобие»
Вероятность (probability), в непрерывном случае 257—258
Вероятность (probability), в. и статистические распределения 259—260
Вероятность (probability), важность точного описания множества элементарных исходов (примеры 7.1—2) 253—256
Вероятность (probability), важность точного описания множества элементарных исходов (упражнения 7.6, 7.11) 271—272
Вероятность (probability), геометрическая в. (пример 7.4) 258
Вероятность (probability), геометрическая в. (упражнения 7.9—11) 272
Вероятность (probability), исчисление в. 250—274
Вероятность (probability), основные правила 252—253
Вес, распределение мужчин по в. (таблица 1.10) 26
Вист, распределение карт при игре в в. (таблица 5.5) 191
Возвращение (replacement), выбор с и без в. 287
Возвращение (replacement), выбор с и без в. (пример 9.12) 312—313
Возвращение (replacement), выбор с и без в. (упражнения 9.8—9) 316
| Волд (Wold H.), критерий Карлемана для проблемы моментов в случае многомерных распределений 160
Волд (Wold H.), поправки Шеппарда 113 117—118 121
Волд (Wold H.), таблица случайных нормальных отклонений 299
Вторая предельная теорема (Second Limit theorem) 165—167
Ву (Woo T.L.), данные о черепах (таблица 1.18) 46
Выбор (sampling) билетов или лотерея 296
Выбор (sampling) из гипотетической совокупности 288
Выбор (sampling) из непрерывных совокупностей 304—305
Выбор (sampling) с и без возвращения 287 см.
Выборочное распределение (sampling distribution) 265—266 см.
Выборочное распределение (sampling distribution) многомерное 373
Выборочное распределение (sampling distribution), аналитический способ нахождения 341—351
Выборочное распределение (sampling distribution), аппроксимация в.р. 380—445
Выборочное распределение (sampling distribution), геометрический способ нахождения 351—359
Выборочное распределение (sampling distribution), отношений 367—373
Выборочное распределение (sampling distribution), отыскание в.с. сумм с помощью метода индукции 365—367
Выборочное распределение (sampling distribution), получение с помощью х.ф. 359—365
Выборочное распределение (sampling distribution), роль в выборочной теории 311
Выборочное распределение (sampling distribution), точные в.р. 341—379
Выборочные моменты (sampling moments) см. «k-статистики»
Вырожденное распределение (unit distribution), х.ф. (пример 4.3) 143
Гамбел (Gumbel E.J.), двумерные ф.р. (упражнение 1.22) 53
Гамбел (Gumbel E.J.), редуцированный размах и редуцированная. средина размаха 469—471
Гамбел (Gumbel E.J.), таблицы распределений крайних значений 470—471
Гамбел (Gumbel E.J.), теория экстремальных (крайних) значений 453 (сноска) 456 460—461
Гамбел (Gumbel E.J.), функция распределения размаха (упражнение 14.19) 476
Гамбургер (Hamburger H.), проблема моментов 157 (сноска)
Гамма-распределение (Gamma distribution), как распределение квадрата нормальной случайной величины (упражнение 4.18) 170
Гамма-распределение (Gamma distribution), логарифмическое преобразование (Джонсона) (упражнение 6.13) 247
Гамма-распределение (Gamma distribution), однозначное определение по моментам (упражнение 4.6) 168
Гамма-распределение (Gamma distribution), приближение к нормальному (пример 6.4) 233—234
Гамма-распределение (Gamma distribution), разложение Грам-Шарлье типа А (пример 6.3) 227—228
Гамма-распределение (Gamma distribution), связь с полиномами Лагерра при разложении в ряд 228
Гамма-распределение (Gamma distribution), семиинварианты и обращение х.ф. (пример 4.4) 143—144 см.
Гамма-распределение (Gamma distribution), характеризация (упражнение 15.22) 509
Гарвуд (Garwood F.), аппроксимация  -распределения (таблица 16.1) 516 -распределения (таблица 16.1) 516
Гаусс (Gauss C.) и нормальное распределение 192 (сноска)
Гаусса — Винклера неравенство (Gauss — Winckier inequality) (упражнение 3.18) 134
Гейен (Gayen A.K.), z-преобразование коэффициента корреляции 540 (сноска)
Генеральная совокупность (population) как основное понятие статистической теории 15
Генеральная совокупность (population), гипотетическая г.с. 39
Генеральная совокупность (population), существующая г.с. 38—39
Генеральная совокупность (population), типы г.с. 287—288
Геометрические вероятности (geometric probabilities) (пример 7.4) 258
Геометрические вероятности (geometric probabilities) (упражнения 7.9—11) 272
Гёльдера неравенство (Holder’s Inequality) 62
Гёльдера неравенство (Holder’s Inequality) (упражнение 3.15) 133
Гипергеометрическое распределение (hypergeometric distribution) 188—191
Гипергеометрическое распределение (hypergeometric distribution) при выборе для изучения качественных признаков (пример 9.12) 312—313
Гипергеометрическое распределение (hypergeometric distribution), предельные формы 197—198
Гипергеометрическое распределение (hypergeometric distribution), факториальные моменты (упражнение 5.26) 207
Гипергеометрическое распределение (hypergeometric distribution), х.ф. и моменты 189—190
Гипотезы 280—283
Гипотетическая совокупность (hypothetical population) 39
Гипотетическая совокупность (hypothetical population), выбор из нее 288
Гири (Geary R.C.), независимость среднего и дисперсии выборки из нормальной генеральной совокупности (пример 12.7) 401—402
Гири (Geary R.C.), независимость среднего и дисперсии выборки из нормальной генеральной совокупности (упражнение 11.19) 377—378
Гири (Geary R.C.), распределение отношения 369
Гири (Geary R.C.), распределение отношения (упражнение 11.11) 375—376
Гистограммы (histogram) 19
Гистограммы (histogram) двумерные 39-41
Главное значение (principal value) в связи с математическим ожиданием 89 (сноска)
Главное значение (principal value) в связи с математическим ожиданием (упражнение 7.19) 274
Годвин (Godwin H.J.), моменты порядковых статистик 450
Годвин (Godwin H.J.), неравенства чебышевского типа 130
Годвин (Godwin H.J.), распределение среднего отклонения 334
Гомоскедастичность (homoscedastic) 530
Госсет (Gosset W.S.) см. «Стьюдент»
Грам-Шарлье ряды (Gram-Charlier series) двумерные 244
Грам-Шарлье ряды (Gram-Charlier series) двумерные (упражнение 6.16) 248
Грам-Шарлье ряды (Gram-Charlier series) двумерные (упражнения 6.10—11) 246—247
Грам-Шарлье ряды (Gram-Charlier series) типа А 219—228
Грам-Шарлье ряды (Gram-Charlier series) типа А (упражнение 6.8) 246
Грам-Шарлье ряды (Gram-Charlier series), подгонка к данным о бобах (пример 6.2) 224—225
Грам-Шарлье ряды (Gram-Charlier series), распределение сумм 228 см.
Грам-Шарлье ряды (Gram-Charlier series), распределение сумм (упражнение 11.10) 375
Грам-Шарлье ряды (Gram-Charlier series), соответствующие ф.р. 224
Грам-Шарлье ряды (Gram-Charlier series), условия сходимости 225—227
Грам-Шарлье ряды (Gram-Charlier series), условия сходимости (упражнение 6.9) 246
Графическое представление частотных распределений (graphical representation of frequency-distributions) см. «Полигон частот» «Гистограмма»
Гринберг (Greenberg B.), таблица дисперсий порядковых статистик в нормальном случае 452
Гринвуд (Greenwood M.), данные о несчастных случаях на производстве (таблица 5.3) 183
Гулдберг (Guldberg S.), семиинварианты многомерных распределений (упражнение 5.19) 206
Гэлбран (Galbrun H.), сходимость рядов Грам-Шарлье 226
Дайсон (Dyson F.J.), эксцесс (упражнение 3.20) 134
Даниэлс (Daniels H.E.), метод перевала 373—374
Даниэлс (Daniels H.E.), распределение отношений 369
Даниэлс (Daniels H.E.), распределение отношений (упражнение 11.24) 379
Датчик случайных чисел (randomizing machine) (пример 9.3) 291—292
Двойное экспоненциальное (Лапласа) распределение (double exponential (Laplace) distribution), дисперсия средней широты (пример 14.5) 469
Двойное экспоненциальное (Лапласа) распределение (double exponential (Laplace) distribution), обращение х.ф. (упражнение 4.3) 168
Двумерное (binomial distribution) 199—201
Двумерное (binomial distribution) нормальное распределение (normal distribution) (пример 1.1) (пример 3.17) 121
Двумерное (binomial distribution) нормальное распределение (normal distribution) как предел двумерного биномиального распределения 200—201
Двумерное (binomial distribution) нормальное распределение (normal distribution), выбор из д.н.р. 529—544
Двумерное (binomial distribution) нормальное распределение (normal distribution), двумерные ряды Грам-Шарлье и дифференциальное уравнение (упражнения 6.16—17) 248
Двумерное (binomial distribution) нормальное распределение (normal distribution), дисперсии и ковариации k-статистик (пример 15.1) 481
Двумерное (binomial distribution) нормальное распределение (normal distribution), дисперсии и ковариации k-статистик (упражнения 13.1—2 и 13.7—8) 443 444
Двумерное (binomial distribution) нормальное распределение (normal distribution), моменты (пример 3.19) 126
Двумерное (binomial distribution) нормальное распределение (normal distribution), моменты ковариации выборки (пример 13.3) 442—443
Двумерное (binomial distribution) нормальное распределение (normal distribution), недостаточность знания одномерных нормальных распределений (упражнение 15—20) 508
Двумерное (binomial distribution) нормальное распределение (normal distribution), однозначность определения по моментам (упражнение 4.17) 170
Двумерное (binomial distribution) нормальное распределение (normal distribution), пуассоновское распределение (упражнение 5.11)
Двумерное (binomial distribution) нормальное распределение (normal distribution), распределение коэффициента корреляции выборки 529—543
Двумерное (binomial distribution) нормальное распределение (normal distribution), распределение коэффициентов регрессии выборки 542—544
Двумерное (binomial distribution) нормальное распределение (normal distribution), распределение отношения случайных величин (упражнение 11.22) 378—379
Двумерное (binomial distribution) нормальное распределение (normal distribution), совместная х.ф. квадратов величин (упражнение 4.19) 170
Двумерное (binomial distribution) нормальное распределение (normal distribution), теорема Шеппарда с медианой дихотомии 485
Двумерное (binomial distribution) нормальное распределение (normal distribution), теорема Шеппарда с медианой дихотомии (упражнения 15.7—8) 506—507
Двумерное (binomial distribution) нормальное распределение (normal distribution), условная ковариация при линейных связях (упражнение 15.18) 508
Двумерное (binomial distribution) нормальное распределение (normal distribution), х.ф. суммы случайных величин (упражнение 7.13) 273
Двумерное (bivariate) биномиальное распределение
Двумерные (bivariate) распределения (distributions) 39—44
Двумерные (bivariate) распределения (distributions) (упражнение 1.22) 53
Двумерные (bivariate) распределения (distributions), k-статистики (k-statistics) 424—430
Двумерные (bivariate) распределения (distributions), подгонка 244
Двумерные моменты и семиинварианты (moments and cumulants) 120—124
Двумерные моменты и семиинварианты (moments and cumulants), стандартные ошибки их 327—328
Дербин (Durbin J.), полиномы Якоби в разложении бета-распределения 229
Децили (deciles) 65 см.
Децили (deciles), интердецильная широта 67
Децили (deciles), стандартные ошибки д. 337
Джеймс (James G.S.), преобразование случайной переменной (упражнение 13.6) 444
Джеймс (James G.S.), разложение суммы квадратов 497
Дженкинсон (Jenkinson A.F.), асимптотическое распределение экстремальных значений 454
Джеффрейс (Sir Harold Jeffreys) и постулат Байеса 277 (сноска)
Джини (Gini C.), коэффициент рассеяния 75
Джини (Gini C.), коэффициент средней разности 74 333—335
Джонсон (Johnson N.L.), моменты дисперсионного отношения 414
Джонсон (Johnson N.L.), моменты порядковых статистик 452
Джонсон (Johnson N.L.), моменты порядковых статистик (упражнения 14.1 и 14.3) 472—473
Джонсон (Johnson N.L.), подгонка двумерных распределений 244
Джонсон (Johnson N.L.), система преобразований вариант 234—235 239 242
Джонсон (Johnson N.L.), среднее отклонение биномиального распределения (упражнение 5.4) 202
Джонсона преобразования (Johnson transformations) 234—243
Джонсона преобразования (Johnson transformations) к данным об облачности (пример 6.6) 239—240
Джонсона преобразования (Johnson transformations), использование при подгонке распределения к данным о бобах (примеры 6.5, 6.7) 237—238 241—242
Джонсона преобразования (Johnson transformations), применение к гаммараспределению (упражнение 6.13) 247
Джэксон (Jackson D.) о медиане 63
Дискретные распределения (discontinuous distributions) 21—23 28—29 32
Дискретные распределения (discontinuous distributions), обращение соответствующих им х.ф. 140—141
Дисперсионного отношения распределение (variance-ratio distribution) (пример 11.20) 369—371
Дисперсионного отношения распределение (variance-ratio distribution), аппроксимации z-распределения 525—528
Дисперсионного отношения распределение (variance-ratio distribution), вид F-распределения 523
Дисперсионного отношения распределение (variance-ratio distribution), моменты F-распределения (упражнение 16.1) 544
Дисперсионного отношения распределение (variance-ratio distribution), общие сведения 521—529
Дисперсионного отношения распределение (variance-ratio distribution), отношение к нормальному, 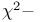 и t-распределению 528—529 и t-распределению 528—529
Дисперсионного отношения распределение (variance-ratio distribution), отношение между F- и z-распределениями 522—523
Дисперсионного отношения распределение (variance-ratio distribution), приближение z-распределения к нормальному 524
Дисперсионного отношения распределение (variance-ratio distribution), распределение в случае коррелированных нормальных случайных величин (упражнение 16.16) 546—547
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 ,
,  ,
, 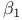 ,
, 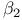
 -распределение
-распределение 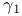 ,
, 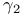
 — величина, служащая критерием при различении типа распределений Пирсона
— величина, служащая критерием при различении типа распределений Пирсона  и t-распределению
и t-распределению