|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Кендалл М., Стюарт А, — Теория распределений |
|
|
 |
| Предметный указатель |
Нормальное распределение (normal distribution), квадратичные формы от нормальных случайных величии 489—500
Нормальное распределение (normal distribution), комбинаторные правила для k-статистик (упражнения 13.10—11) 444—445
Нормальное распределение (normal distribution), математические ожидания отношений моментов (упражнение 11.5) 374
Нормальное распределение (normal distribution), методы оценки стандартного отклонения исходного распределения 332
Нормальное распределение (normal distribution), моменты вероятностей (упражнение 5.10) 203—204
Нормальное распределение (normal distribution), моменты и п.ф.м. (пример 3.4) 90
Нормальное распределение (normal distribution), моменты медианы и других порядковых статистик 447—450
Нормальное распределение (normal distribution), моменты медианы и других порядковых статистик (пример 14.1) 451—452
Нормальное распределение (normal distribution), моменты медианы и других порядковых статистик (упражнение 14.14) 475
Нормальное распределение (normal distribution), моменты среднего отклонения 333—334
Нормальное распределение (normal distribution), моменты средней разности 334—335
Нормальное распределение (normal distribution), независимость среднего выборки и любой другой k-статистики как характеристическое свойство, некоррелированность среднего выборки и любой другой k-статистики как характеристическое свойство (упражнение 12.20) 423
Нормальное распределение (normal distribution), независимость среднего и дисперсии выборки как характеристическое свойство (пример 11.7) 354—355
Нормальное распределение (normal distribution), независимость среднего и дисперсии выборки как характеристическое свойство (пример 12.7) 401—402
Нормальное распределение (normal distribution), независимость среднего и дисперсии выборки как характеристическое свойство (примеры 15.4—6) 495—496 499 500—503
Нормальное распределение (normal distribution), некоррелированность k-статистик (пример 12.5) 400
Нормальное распределение (normal distribution), неравенство для интеграла от нормальной плотности (упражнение 15.5) 506
Нормальное распределение (normal distribution), нормальность распределения линейной функции от независимых нормальных случайных величин (пример 11.2) 346—347
Нормальное распределение (normal distribution), нормальность распределения линейной функции от независимых нормальных случайных величин (пример 11.5) 352—353
Нормальное распределение (normal distribution), обращение х.ф. (пример 4.1) 141—142
Нормальное распределение (normal distribution), однозначность определения по моментам (пример 4.7) 160
Нормальное распределение (normal distribution), отношение между нормальным и связанными с ним распределениями 528—529
Нормальное распределение (normal distribution), подгонка к данным о ростах (таблица 5.6) 196
Нормальное распределение (normal distribution), распределение отношения нормальных случайных величин (пример 11.21) 372—373
Нормальное распределение (normal distribution), распределение отношения нормальных случайных величин (упражнение 11.11) 375—376
Нормальное распределение (normal distribution), распределение отношения нормальных случайных величин (упражнение 11.22) 378—379
Нормальное распределение (normal distribution), распределение отношения случайного отклонения от среднего выборки к стандартному отклонению выборки (упражнение 16.20) 547 см. «Многомерное
Нормальное распределение (normal distribution), распределение размаха и его таблицы 452
Нормальное распределение (normal distribution), распределение среднего выборки (пример 11.12) 361
Нормальное распределение (normal distribution), распределение среднего выборки (пример 11.7) 354—355
Нормальное распределение (normal distribution), распределение суммы квадратов 342—343
Нормальное распределение (normal distribution), распределение суммы квадратов (пример 11.16) 364—365
Нормальное распределение (normal distribution), распределение суммы квадратов (пример 11.18) 366—367
Нормальное распределение (normal distribution), распределение суммы квадратов (пример 11.6) 353—354
Нормальное распределение (normal distribution), распределение экстремального значения (пример 14.3) 548
Нормальное распределение (normal distribution), распределения, связанные с нормальным 510—548
Нормальное распределение (normal distribution), семиинварианты (пример 3.11) 108—109
Нормальное распределение (normal distribution), случайные нормальные отклонения 299
Нормальное распределение (normal distribution), среднее отклонение 196
Нормальное распределение (normal distribution), стандартная ошибка медианы (пример 10.7) 330—331
Нормальное распределение (normal distribution), стандартная ошибка семиинтерквартильной широты (пример 10.8) 332
Нормальное распределение (normal distribution), таблицы моментов порядковых статистик 452
Нормальное распределение (normal distribution), ф.р. 192—193
Нормальное распределение (normal distribution), ф.р. (упражнения 5.12—18) 204—206
Нормальное распределение (normal distribution), х.ф. квадрата нормальной случайной величины (упражнение 4.18) 170
Нормальное распределение (normal distribution), х.ф. совместного распределения нормальной случайной величины и ее квадрата (упражнение 7.15) 273
Нормальное распределение (normal distribution), характеризации нормального распределения 500—506
Нормальное распределение (normal distribution),таблицы 195—196
Нормированное распределение (standard measure) 74—75
Нормированное распределение (standard measure), преобразование семиинвариантов при переходе к н.р. 100—101
Нормированное распределение (standard measure), преобразование х.ф. при переходе к н.р. (пример 4.6) 153—165
Нормированное распределение (standard measure), преобразование х.ф. при переходе к н.р. (пример 4.9) 166—167
Нэйр (Nair U.S.), моменты средней разности 335
Облачность, данные об интенсивности о. (таблица 1.11) 26
Облачность, подгонка с помощью преобразования Джонсона и распределений Пирсона I типа (пример 6.6) 239—240
Обратные вероятности (inverse probability) см. «Байеса теорема»
Обратный выбор для изучения качественных признаков (inverse sampling for attributes) (пример 9.13) 313—314
Ожидание, среднее значение (expectation, expected value) 79—80
Ортогональные полиномы Лаггера и Якоби 228—229
Ортогональные полиномы Чебышева — Эрмита 217—219
Ортогональные преобразования 346—347
Ортогональные преобразования, характеристическое свойство нормального распределения 504—505
Ортогональные преобразования, Хельмерта о.п. (пример 11.3) 347—348
Отношение, моменты 413—414
Отношение, распределение 367—373
Отношение, распределение (упражнения 11.11—13, 11.22) 375—377 378—389
Отношение, стандартная ошибка о. 324
Отрицательное биномиальное распределение (negative binomial distribution) 185—186
Отрицательное биномиальное распределение (negative binomial distribution) в последовательном выборе для изучения качественных признаков (пример 9.13) 313—314
Отрицательное биномиальное распределение (negative binomial distribution) в последовательном выборе для изучения качественных признаков (упражнение 9.12) 316
Отрицательное биномиальное распределение (negative binomial distribution) как комбинация пуассоновского и логарифмического распределений (упражнение 5.21) 206
Отрицательное биномиальное распределение (negative binomial distribution) как пауссоновское распределение со случайным параметром, имеющим распределение типа III 184
Отрицательное биномиальное распределение (negative binomial distribution), х.ф. и семиинварианты 186
Отрицательное экспоненциальное распределение (negative exponential distribution) см. «Экспоненциальное распределение»
Оуэн (Owen D.B.), многомерный нормальный интеграл 483
Оуэн (Owen D.B.), таблицы гипергеометрического распределения 191
Оценивание (estimation) в случае больших выборок 312
Оценивание (estimation) при изучении качественных признаков 305—314
Ошибки (errors) см. «Стандартные ошибки»
П.ф.м., производящая функция моментов (moment-generating function) 91—93
П.ф.с, производящая функция семиинвариантов (cumulant-generating function) 100
П.ф.ф.м., производящая функция факториальных моментов (factorial moment-generating function) 98—99
П.ф.ф.м., производящая функция факториальных моментов (factorial moment-generating function), обращение (упражнение 3.24) 135
Параметры (parameters) 55
Парето кривая (Pareto curve) и средняя разность (упражнение 2.19) 82
Первая предельная теорема (First limit theorem) 149—151
Первая предельная теорема (First limit theorem), обращение 151—153
Перевала метод, использование при построении аппроксимации 373—374 471
Перестановки случайные (random permutations) (пример 9.7) 302
Пирс (Pearce Т.V.), данные (таблица 1.22) 48
Пирс (Pearse G.E.), данные (таблица 1.11) 26
Пирсон Е. (Pearson E.S.), выборочное распределение 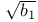 411—413 411—413
Пирсон Е. (Pearson E.S.), выборочное распределение 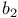 (упражнение 12.10) 421 (упражнение 12.10) 421
Пирсон Е. (Pearson E.S.), распределение отношения случайного отклонения от среднего к стандартному отклонению выборки (упражнение 16.20) 547
Пирсон Е. (Pearson E.S.), распределение размаха 466 471
Пирсон Е. (Pearson E.S.), таблицы  512 512
Пирсон Е. (Pearson E.S.), таблицы распределения размаха 466 471
Пирсон К. (Pearson K.), данные о плодовитости конематок (таблица 1.19) 46
Пирсон К. (Pearson K.), данные о распределении карт в висте (таблица 5.5) 191
Пирсон К. (Pearson K.), данные о трипанозомах (таблица 1.13) 28
Пирсон К. (Pearson K.), коэффициент вариации 75
Пирсон К. (Pearson K.), критерий согласия  и и  -распределение 492 -распределение 492
Пирсон К. (Pearson K.), мера асимметрии 124 210
Пирсон К. (Pearson K.), моменты биномиального распределения (упражнение 5.5) 202
Пирсон К. (Pearson K.), моменты порядковых статистик в нормальном случае 450
Пирсон К. (Pearson K.), неравенство чебышевского типа 129
Пирсон К. (Pearson K.), поправки к группировке 117
Пирсон К. (Pearson K.), разложение варианты в терминах ее ф.р. 450—451
Пирсон К. (Pearson K.), распределение разности случайных переменных III типа (упражнение 11.15) 377
Пирсон К. (Pearson K.), табулирование тетрахорических функций 225
Пирсоновские распределения (Pearson distributions) ,рекуррентные соотношения между моментами 209
Пирсоновские распределения (Pearson distributions) как предел гипергеометрических 198
Пирсоновские распределения (Pearson distributions), асимметрия 210
Пирсоновские распределения (Pearson distributions), критерий для различения типа 212
Пирсоновские распределения (Pearson distributions), общие сведения 208—216
Пирсоновские распределения (Pearson distributions), подгонка 214—216
Пирсоновские распределения (Pearson distributions), рекуррентные соотношения для х.ф. и семиинвариантов (упражнение 6.7) 246 см.
Питмэн (Pitman E.J.G.), моменты коэффициента корреляции выборки в случае независимых наблюдений (упражнение 6.17) 547
Питмэн (Pitman E.J.G.), производные х.ф. и моменты 163
Питмэн (Pitman E.J.G.), характеристическое свойство гамма-распределения (упражнение 15.22) 509
Плодовитость, распределение конематок в соответствии с п. (таблица 1.19) 46
Плэкетт (Plackett R.L.), границы для среднего значения размаха 467
Плэкетт (Plackett R.L.), многомерный нормальный интеграл 483
Подвыборки среднее значение (subsample mean), стандартная ошибка в разности между средними выборки и подвыборки (упражнение 10.20) 339
Подоходный налог, распределение лиц в соответствии с п.н. 18 19 31
Пойа (Polya Q.), неравенство для нормального интеграла (упражнение 5.17) 206
Пойа (Polya Q.), нормальная ф.р. (упражнение 5.18) 206
Пойа (Polya Q.), Пойа — Эйпли распределение (упражнение 5.8) 203
Полигон частот (frequency polygon) 19
Полигон частот (frequency polygon), двумерный случай 39—41
Полсон (Paulson E.), нормализация распределения дисперсионного отношения 527—528
Поправки к группировке (corrections for grouping) 57 72—73 111—120 124
Поправки к группировке (corrections for grouping) (упражнения 3.10, 3.13) 132 см.
Порядковые статистики (order-statistics) 349 446—476
Порядковые статистики (order-statistics), асимптотические распределения 452—461
Порядковые статистики (order-statistics), асимптотические распределения (упражнение 14.21) 476
Порядковые статистики (order-statistics), верхние границы для ожидаемых значений 462—463
Порядковые статистики (order-statistics), дисперсия (упражнение 14.6) 473
Порядковые статистики (order-statistics), моменты в нормальном случае 447—450
Порядковые статистики (order-statistics), размах и средина размаха 464—471
Порядковые статистики (order-statistics), распределение 319—351
Порядковые статистики (order-statistics), реккурентные соотношения между моментами и распределениями 461
Порядковые статистики (order-statistics), реккурентные соотношения между моментами и распределениями (упражнение 14.5) 473
Порядковые статистики (order-statistics), совместное распределение (упражнение 11.7) 50 446 463 446—476
Порядковые статистики (order-statistics), таблицы в нормальном случае 452
Порядковые статистики (order-statistics), таблицы распределений крайних значений 479
Последовательный выбор при изучении качественных признаков (sequential sampling for attributes) (пример 9.13) 313—314
Правдоподобие (likelihood) 276
Правдоподобие (likelihood) и теорема Байеса 280—283
Правдоподобие (likelihood) и теорема Байеса (упражнение 8.1—2) 284—285
| Правдоподобие (likelihood), принцип м.п. в случае выбора для изучения качественных признаков (упражнения 9.5, 9.10) 315 316
Правдоподобие (likelihood), принцип максимального правдоподобия 280—284
Правило следования Лапласа (succession rule of Laplace) (пример 8.3) 278—279
Правило следования Лапласа (succession rule of Laplace) (упражнение 8.4) 285
Предельные теоремы (limit theorems) см. «Первая предельная теорема» «Вторая «Центральная «Больших
Предложения, распределение по их длине (таблица 1.17) 46
Предсказание урожая, пристрастие (систематическая ошибка) при п.у., (пример 9.4) 292—293
Преобразования 35—37 43—45 342—344
Преобразования ортогональные 346—348
Преобразования, коэффициент корреляции см. «Корреляции коэффициент»
Преобразования, оставляющие порядки величин семиинвариантов без изменения (упражнение 13.6) 444
Преобразования, п., уравнивающие дисперсию (упражнение 10.17) 339
Преториус (Pretorius S.T.), данные о бобах (таблица 1.15) 40
Преториус (Pretorius S.T.), данные о бобах (таблица 6.1)
Преториус (Pretorius S.T.), данные об австралийских свадьбах (таблица 1.8) 24
Преторнус (Pretorius S.T.), двумерные распределения 223
Пристрастие (bias) (систематическая ошибка) 289—294
Пристрастие (bias) (систематическая ошибка) в предсказании урожая (пример 9.4) 292—293
Пристрастие (bias) (систематическая ошибка) при выборе растений (пример 9.1) 289—290
Пристрастие (bias) (систематическая ошибка) при считывании результатов случайного эксперимента (пример 9.3) 291—292
Пристрастие (bias) (систематическая ошибка) при считывании со шкал (пример 9.2) 290—291
Проблема моментов (problem of moments) (упражнение 3.12) 132
Проблема моментов (problem of moments), общие сведения 156—161 166—167
Проблема моментов (problem of moments), общие сведения (упражнения 4.13, 4.17) 169 170
Проблема моментов (problem of moments), п.м. и сходимость рядов типа А (упражнение 6.9) 246
Производящая функция моментов (moment-generating functions) (н. ф. м.) 91—93
Производящая функция частот (frequencygenerating function) 45
Производящая функция частот (frequencygenerating function), дисперсии (пример 2.9) 72
Производящая функция частот (frequencygenerating function), нахождение среднего (пример 2.3) 58
Простой случайный выбор (simple random sampling) 286—287
Прямоугольное распределение (uniform distribution) см. «Равномерное распределение»
Псевдослучайные числа (pseudo-random numbers) 304
Пуассоновское распределение (Poisson distribution) в сочетании с логарифмическим распределением (п. р.) приводит к отрицательному биномиальному распределению (упражнение 5.21) 206
Пуассоновское распределение (Poisson distribution) при изучении качественных признаков (упражнение 9.5) 315
Пуассоновское распределение (Poisson distribution) со случайным параметром (упражнение 4.16) 170 183—188
Пуассоновское распределение (Poisson distribution) трехмерное (упражнение 5.11) 204
Пуассоновское распределение (Poisson distribution), моменты (упражнение 3.1) 130
Пуассоновское распределение (Poisson distribution), общие сведения 178—185
Пуассоновское распределение (Poisson distribution), однозначность определения по моментам (упражнение 4.4) 168
Пуассоновское распределение (Poisson distribution), производящая функция частот (упражнение 1.13) 52
Пуассоновское распределение (Poisson distribution), разбиение совокупности на группы и распределение Пойа — Эйпли (упражнение 5.8) 203
Пуассоновское распределение (Poisson distribution), разность двух пуассоновских вариант (упражнение 3.8) 131
Пуассоновское распределение (Poisson distribution), распределение временных интервалов (упражнение 16.6) 545
Пуассоновское распределение (Poisson distribution), распределение Неймана типа А со случайными параметрами как результат комбинации двух пуассоновских распределений (упражнение 5.7) 203
Пуассоновское распределение (Poisson distribution), распределение среднего, выборки (пример 11.11) 360
Пуассоновское распределение (Poisson distribution), смесь распределений 180—185
Пуассоновское распределение (Poisson distribution), сумма независимых пуассоновских величин есть пуассоновская величина (упражнение 7.14) 273
Пуассоновское распределение (Poisson distribution), сходимость к нормальному распределению (пример 4.9) 166—167
Пуассоновское распределение (Poisson distribution), условное в связи с критерием согласия  (упражнение 15.21) 508—509 (упражнение 15.21) 508—509
Пуассоновское распределение (Poisson distribution), ф.р. и таблицы 179—180
Пуассоновское распределение (Poisson distribution), факториальные моменты (упражнение 5.26) 207
Пуассоновское распределение (Poisson distribution), х.ф. и семиинварианты (пример 3.10) 108 178—179
Пуассоновское распределение (Poisson distribution), х.ф. суммы случайного числа (с п.р.) случайных величин (упражнение 5.22) 206
Пшеницы растения, распределение по высоте (таблицы 9.1) 289
Пэрмэн (Pairman E.), поправки к группировке 117
Равномерное распределение (rectangular, distribution) дискретное (х.ф. и семиинварианты) (упражнение 3.23) 135
Равномерное распределение (rectangular, distribution), дисперсия медианы (пример 14.2) 452
Равномерное распределение (rectangular, distribution), дисперсия медианы (упражнение 10.15) 339
Равномерное распределение (rectangular, distribution), дисперсия среднего отклонения (упражнение 10.19) 339
Равномерное распределение (rectangular, distribution), дисперсия, среднее отклонение и средняя разность (упражнение 2.5) 81
Равномерное распределение (rectangular, distribution), моменты средней разности 335
Равномерное распределение (rectangular, distribution), преобразования к р.р. 37
Равномерное распределение (rectangular, distribution), преобразования к р.р. (упражнение 1.21) 53
Равномерное распределение (rectangular, distribution), распределение отношения наибольших значений (упражнение 11.20) 378
Равномерное распределение (rectangular, distribution), распределение произведения наибольших значений (упражнение 11.21) 378
Равномерное распределение (rectangular, distribution), распределение произведения равномерно распределенных случайных величин (упражнение 11.6) 374—375
Равномерное распределение (rectangular, distribution), распределение произведения равномерно распределенных случайных величин (упражнение 16.4) 544
Равномерное распределение (rectangular, distribution), распределение среднего геометрического (пример 11.15) 363—364
Равномерное распределение (rectangular, distribution), распределения порядковых статистик, бета-распределение 447
Равномерное распределение (rectangular, distribution), распределения порядковых статистик, распределение отношения средины размаха к размаху (упражнение 14.17) 475
Равномерное распределение (rectangular, distribution), распределения порядковых статистик, распределение размаха (упражнение 14.16) 475
Равномерное распределение (rectangular, distribution), распределения порядковых статистик, распределение разности двух средних размаха (упражнение 14.18) 475—476
Равномерное распределение (rectangular, distribution), распределения порядковых статистик, распределение средины размаха (упражнение 14.13) 474—475
Равномерное распределение (rectangular, distribution), распределения порядковых статистик, совместное распределение размаха и средины размаха (упражнение 14.12) 474
Равномерное распределение (rectangular, distribution), точное распределение среднего выборки (пример 11.14) 361—362
Равномерное распределение (rectangular, distribution), точное распределение среднего выборки (пример 11.9) 357—359
Равномерное распределение (rectangular, distribution), х.ф. и семиинварианты (упражнение 3.23) 135
Разложение суммы квадратов (decomposition of sums of squares) 497—500
Разложение суммы квадратов (decomposition of sums of squares) (упражнение 15.16—17) 508
Размах (range) 67—68
Размах (range), асимптотическое распределение 467—469
Размах (range), асимптотическое распределение (упражнение 14.20) 476
Размах (range), границы для математического ожидания 466—467
Размах (range), редуцированный размах 469—471
Размах (range), существование математического ожидания (упражнение 14.15) 475
Размах (range), точное распределение 464—466
Размах (range), точное распределение (упражнение 14.19) 476
Райдер (Rider P.R.), распределение произведения наибольших значений в выборках из равномерных распределений (упражнение 11.21) 378
Рао см. «Кендалл Д.»
Расположение (location), меры р. 54—67
Распределение, зависящее от случайных параметров (contagious distribution) см. «Типа А распределение»
Рассеяние (dispersion), меры р. 67—79
Рассеяния коэффициент (concentration coefficient) 75—77
Рассеяния коэффициент (concentration coefficient), кривая рассеяния 76
Рассеяния матрица (dispersion matrix) 480—481
Рассеяния матрица (dispersion matrix) (упражнения 15.1—3, 15.9—11) 506 507
Расширенные симметрические функции (augmented symmetric functions) 382
Рафф (Raff M.S.), ошибка при аппроксимации биномиального распределения нормальным 178
Регрессия (regression), в линейной регрессионной модели (упражнение 16.5) 544—545
Регрессия (regression), коэффициенты 541—542
Регрессия (regression), линейность в случае двумерного нормального распределения 529—530
Регрессия (regression), распределение коэффициентов в случае выборки из генеральной совокупности с двумерным нормальным распределением 542—544
Регрессия (regression), стандартные ошибки коэффициентов р. (упражнение 16.13) 546
Редуцированные размах и средина размаха (reduced range and midrange) 469—471
Романовский В., о моментах биномиального распределения (упражнение 5.2) 202
Рост, распределение мужчин по ростам (таблица 1.7) 23
Рост, распределение мужчин по ростам среднее (пример 2.1) 56—58
Рост, распределение мужчин по ростам, квартили (пример 2.6) 66
Рост, распределение мужчин по ростам, кривая распределения (рис. 2.1) 66
Рост, распределение мужчин по ростам, медиана (пример 2.5) 63
Рост, распределение мужчин по ростам, подгонка с помощью нормального распределения (таблица 5.6) 197
Рост, распределение мужчин по ростам, полигон частот (рис. 1.3) 24
Рост, распределение мужчин по ростам, семиинварианты (пример 3.9) 107
Рост, распределение мужчин по ростам, среднее отклонение и стандартное отклонение (пример 2.7) 70—71
Рост, распределение мужчин по ростам, средняя разность (пример 2.10) 78—79
Рост, распределение мужчин по ростам, стандартная ошибка среднего (пример 10.1) 321
Рост, распределение мужчин по ростам, стандартные ошибки старших моментов (упражнение 10.1) 337
Рост, распределение мужчин по ростам, факториальные и обычные моменты (пример 3.7) 97—98
Рубин (Ruben H.), многомерный нормальный интеграл 488
Рубин (Ruben H.), моменты наибольших порядковых статистик для выборок из нормальной генеральной совокупности 461
Сакамото (Sakamoto H.), характеристическое свойство нормального распределения 502
Самоубийства, данные о с. (таблица 1.6) 22
Самоубийства, с. и пуассоновское распределение 183
Сархан (Sarhan A.E.), таблица дисперсий порядковых статистик в нормальном случае 452
Сас (Szasz O.), условия для х.ф. 147
Свертка (convolution) случайных величин см. «Сумма с.в.»
Семиинварианты (cumulants) многомерные 121—124
Семиинварианты (cumulants) после второго (упражнение 4.11) 169
Семиинварианты (cumulants), вычисление 107—110
Семиинварианты (cumulants), обращение в нуль начиная со второго (пример 4.3) 143
Семиинварианты (cumulants), определение 99—100
Семиинварианты (cumulants), поправки к группировке 119—120 124
Семиинварианты (cumulants), поправки к группировке (упражнение 3.13) 132
Семиинварианты (cumulants), производящая функция с. 100
Семиинварианты (cumulants), свойства инвариантности 100
Семиинварианты (cumulants), связь с моментами 101—106
Семиинварианты (cumulants), стандартные ошибки (пример 10.4) 324
Семиинварианты (cumulants), стандартные ошибки (упражнение 10.12) 338—339
Семиинварианты (cumulants), структурные свойства 438—440 см.
Семиинварианты (cumulants), существование 106—107
Семиинтерквартильная широта (с.и.ш.) (semi-interquartile range) см. «Интерквартильная широта»
Семиннварнаитов производящая функция (п.ф.с.) (cumulant-generating function) или логарифм характеристической функции 100
Сёге (Szego) 228 см.
Сигнум-функция (sgn x) 138
Симметрические функции (symmetric functions), общие сведения 380—390
Симметрические функции (symmetric functions), общие сведения (упражнение 12.19) 423
Симметрические функции (symmetric functions), таблицы 102—103 (сноска) 383
Симметричные распределения (symmetrical distributions) 23—25
Симметричные распределения (symmetrical distributions), верхние границы для средних значений порядковых статистик 462—163
Симметричные распределения (symmetrical distributions), граница для дисперсии медианы (упражнение 14.7) 474
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



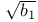
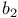 (упражнение 12.10)
(упражнение 12.10) 