|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hughes B.D. — Random Walks and Random Environments: Random Environments (том 2) |
|
|
 |
| Предметный указатель |
AB percolation 55
Acceptance profile 63
Admissible current distribution 323
Admissible potential distribution 321
Alexander — Orbach conjecture 364 458—465 467
Alexander — Orbach scaling law 459 481
Animals See Lattice animals
Ant in the labyrinth, above percolation threshold 442—443 481
Ant in the labyrinth, at percolation threshold 443—444
Ant in the labyrinth, below percolation threshold 439—442
Ant in the labyrinth, biased 452
Ant in the labyrinth, defined 437
Ant in the labyrinth, dynamical scaling theories, dominant time scales 450—451 456—457
Ant in the labyrinth, dynamical scaling theories, extensions 451
Ant in the labyrinth, dynamical scaling theories, mean number of distinct sites visited 445—447
Ant in the labyrinth, dynamical scaling theories, mean-square displacement 447—448
Ant in the labyrinth, dynamical scaling theories, other applications 448—450
Ant in the labyrinth, rigorous results at 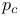 , Bethe lattice 466—467 , Bethe lattice 466—467
Ant in the labyrinth, rigorous results at 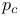 , square lattice 467—468 , square lattice 467—468
Ant in the labyrinth, rigorous results for 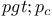 , Bethe lattice 482 , Bethe lattice 482
Ant in the labyrinth, rigorous results for 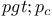 , hypercubic lattice 481 , hypercubic lattice 481
Ant in the labyrinth, Teles' scaling laws 468—481
Ant in the labyrinth, transience above 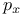 if if 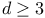 481 481
Ant in the labyrinth, trapping 494
Ant in the labyrinth, variations 496
Ant, blind 438
Ant, myopic 438
Antipercolation 55
Apparent fractal dimension of the backbone 296
Apparent fractal dimension of the infinite cluster 297—298
Arithmetic distribution 404
Backbone probability, bound for conductivity 335
Backbone probability, bounded 94 107
Backbone probability, for Bethe lattice 26—27
Backbone, apparent fractal dimension 296
Backbone, defined 94
Backbone, exponent bounds 107 271
Backbone, few rigorous results 52
Backbone, fractal model 359
Backbone, introduced for Bethe lattice 26
Backbone, node and link model 358
Backbone, node-link-blob model 360
Backbone, picture of 293
Bernoulli percolation models, bond See Bond percolation
Bernoulli percolation models, etymology 4
Bernoulli percolation models, site See Site percolation
Bethe lattice, ant in labyrinth for 466 482
Bethe lattice, backbone probability B(p) 26
Bethe lattice, cluster-size distribution 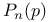 exact for exact for 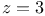 , derivation 37 , derivation 37
Bethe lattice, cluster-size distribution 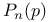 exact for exact for 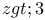 , quoted 37 , quoted 37
Bethe lattice, conduction problem on 343
Bethe lattice, connectivity function 244
Bethe lattice, defined 22
Bethe lattice, Durrett — Nguyen inequality sharp for 216
Bethe lattice, effectively 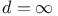 22 22
Bethe lattice, exponents  and and 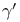 equal 202 equal 202
Bethe lattice, exponents same as periodic lattice above upper critical dimension 50
Bethe lattice, exponents summarized 198
Bethe lattice, free energy 205
Bethe lattice, gelation model 14
Bethe lattice, infinitely many infinite clusters above 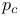 133 133
Bethe lattice, mean cluster size 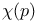 35 35
Bethe lattice, pair connectedness 244
Bethe lattice, percolation probability 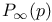 25 25
Bethe lattice, percolation threshold of 35
Bethe lattice, picture of 22
Bethe lattice, problems with concavity of F(p, h) 221
Bethe lattice, relatives of 27 37
Bethe lattice, should take 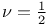 245 245
Bethe lattice, site-bond percolation on 54
Bethe lattice, susceptibility 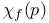 37 37
Bipartite lattice 56 175 464
Bipartite percolation 56
Blind ant 438
Boltzmann distribution 451
Boltzmann's constant 451
Bond bridge 21
Bond bridge, closed, defined 5
Bond bridge, open, defined 5
Bond percolation, clusters in 5
Bond percolation, defined 5
Bond percolation, equivalent to site percolation on covering lattice 13
Bond percolation, exact thresholds for d=2, bow-tie lattice 158
Bond percolation, exact thresholds for d=2, history 142—143
Bond percolation, exact thresholds for d=2, honeycomb lattice 156
Bond percolation, exact thresholds for d=2, overview of proofs 143
Bond percolation, exact thresholds for d=2, square lattice 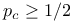 147 147
Bond percolation, exact thresholds for d=2, square lattice 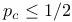 145 145
Bond percolation, exact thresholds for d=2, summarized 142
Bond percolation, exact thresholds for d=2, triangular lattice 156
Bond percolation, pictures of 5—11
Bond percolation, PostScript code to simulate 10
Bond percolation, wet set, cardinality of 11
Bond percolation, wet set, defined 11
Borel — Cantelli lemma 492
Braess's paradox 324
Branch conductance 344
Bridge bond 21
Buckingham — Gunton scaling law 249
Bus bars 326
Cardy's conjecture on crossing probabilities 261—264
Cauchy — Schwarz inequality See also Schwarz inequality
Cauchy — Schwarz inequality, stated 206 219
Cauchy — Schwarz inequality, used 215 219 222 225 227 267 346 413
Cayley tree, conduction problem on 343
Cayley tree, defined 22
Chebyshev's inequality, Markov's inequality as precursor 212
Chebyshev's inequality, used in ergodic theory 132
Chemical distance 476
Cluster shape 51
Cluster-size distribution, 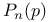 defined 15 defined 15
Cluster-size distribution, decay at low density 38—39
Cluster-size distribution, decay in high-density phase 45—46 125—126
Cluster-size distribution, exponential decay in low-density phase 108—111
Cluster-size distribution, for Bethe lattice 35—37
Commute time 474
Conditional distribution 138
Conditional expectation 114
Conditional expected number of pivotal sites 101
Conditional mean cluster size, given cluster size finite 37
Conditional probability density function for bond conductance after renormalization 351
Conditional probability density function for branch conductance on Bethe lattice 346
Conditional probability distribution for ant's cluster size 439
Conditional probability, 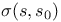 88 98 88 98
Conditional probability, definition recalled 88 101
Conditional probability, in definition of incipient infinite cluster 301
Conditional probability, that occupied site belongs to infinite cluster 28 52
Conditional probability, that open bond belongs to infinite cluster 30
Conditional probability, used 107 114 115 117 137
Conductivity exponent, conjectures 359 360 364—369
Conductivity exponent, dynamical scaling theory for 454
Conductivity exponent, Flory-type argument 361
Conductivity exponent, numerical estimates 369—371
Conductivity, effective 326
Conductivity, microscopic 348
Conductivity, specific 326
Conformal field theory 261
Connective constant, bounding critical probability 16—17
Connective constant, defined 2
Connectivity function, at percolation threshold 238—240
Connectivity function, decay of in low-density phase 97
Connectivity function, defined 88
Connectivity function, for Bethe lattice 244
Connectivity function, in high-density phase 242—244
Connectivity function, moments of 233
Connectivity function, scaling theory for 241
Contact process 69
Continuum percolation 68
Continuum resistance dimension 468
Convex function 328
| Coordination number, defined 2 22
Correlated percolation 58
Correlation length, critical exponent 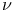 for 231 for 231
Correlation length, defined for percolation 229
Correlation length, definition via moments of pair-connectedness 233
Correlation length, divergence of 230
Correlation length, exponent bounds 231 235—238
Correlation length, in high-density phase 125 243
Correlation length, relevant to ant in labyrinth 454—456
Cover time 476
Covering lattice 12
Critical amplitudes 266 283
critical exponent 2
Critical exponents for percolation, defined,  , ,  and and  198 198
Critical exponents for percolation, defined, 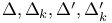 206—207 206—207
Critical exponents for percolation, defined, 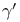 , ,  and and 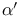 201—204 201—204
Critical exponents for percolation, estimates for d=3 288—289
Critical exponents for percolation, mean-field values 199
Critical exponents for percolation, on Bethe lattice 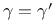 202 202
Critical exponents for percolation, overview 50
Critical exponents for percolation, rigorous scaling inequalities, Durrett and Nguyen 215—216
Critical exponents for percolation, rigorous scaling inequalities, Newman's 218—221
Critical exponents for percolation, scaling theories, alternative forms 211
Critical exponents for percolation, scaling theories, of Essam and Gwilym 211
Critical exponents for percolation, scaling theories, Stauffer's 208—210
Critical exponents for percolation, “exact” values for d=2 284—288
Critical probability, for high-density phase (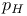 ), defined 15 ), defined 15
Critical probability, for high-density phase (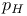 ), lower bound for square lattice bond problem 147—152 ), lower bound for square lattice bond problem 147—152
Critical probability, for high-density phase (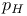 ), lower bound for triangular lattice site problem 161—162 ), lower bound for triangular lattice site problem 161—162
Critical probability, for low-density phase ( ), defined 33 ), defined 33
Critical probability, for low-density phase ( ), upper bound for square lattice bond problem 145—147 ), upper bound for square lattice bond problem 145—147
Critical probability, for low-density phase ( ), upper bound for triangular lattice site problem 162 ), upper bound for triangular lattice site problem 162
Critical probability, for slice, limit of 125 486
Critical probability, sponge-crossing (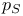 ), defined 124 ), defined 124
Critical probability, sponge-crossing (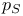 ), equal to ), equal to  and and 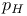 124. See also percolation threshold 124. See also percolation threshold
Criticality Theorem of groadbent and Hammersley 16
Crossing probability, Cardy's conjecture 261
Crossing probability, rigorous result for square lattice bond percolation at 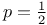 145 145
Decimation 252
Dense lattice 478
Dhar's formula 444 458 462 495
Diffusion constant for continuum diffusion 451—453 468
Diffusion constant for Temkin's model 397
Diffusion constant for the ant in the labyrinth 442 453 456
Diffusion constant on the infinite cluster 443 452 454 456
Diffusion process, contrast with percolation 4
Dimension, continuum resistance 468
Dimension, diode models 419
Dimension, first-passage time 477
Dimension, for infinite cluster 297
Dimension, fractal, apparent for backbone 296
Dimension, fractal, in scaling laws for ant in labyrinth 477
Dimension, fracton 458
Dimension, harmonic 444 445 459 462 464 467 481 495
Dimension, resistance 469 477
Dimension, spectral 444 445 458 459 462 464 467 481 495
Directed percolation See percolation theory variations
Dirichlet's Principle, analogue used 429 430
Dirichlet's Principle, stated and proved 321
Dirichlet's Principle, used 325 327 331 336
Discrete Tauberian Theorem, stated 36
Discrete Tauberian Theorem, used 36 205
Distance, chemical 476
Distance, graphical 476
Distance, stepping 86 89 91 97 230 294 476
Distribution, arithmetic 404
Drag coefficient 451
Dual lattices, applications to random resistor networks 328
Dual lattices, defined 143
Dual lattices, implications on percolation thresholds 152—156
Dynamical phase transition 392
Dynamical scaling theory for conductivity 454—455. See also ant in the labyrinth dynamical
Eden model 68
Effective conductance between sites 321
Effective conductivity 326
Effective conductivity, one dimension 319
Effective conductivity, series and parallel bounds 327
Effective medium approximation, cluster improvements 353
Effective medium approximation, estimates of percolation threshold 353
Effective medium approximation, for bond percolation conduction 352
Effective medium approximation, for site percolation conduction 355
Effective resistance between sites 321
Eigenfunction expansion techniques 393
Eigenvalue, multiple-path diffusion 425
Eigenvalue, renormalization transformation 253
Einstein, Albert 318
Ergodic theorem 131
Ergodic theory, applied to Temkin's model 396
Ergodic theory, introduced 127
Ergodic transformation 129
Euler transformation, used for high-density series 32
Euler transformation, used for low-density series 43
Event approximation lemma, stated but not proved 128
Event approximation lemma, used 129
Event, decreasing 91
Event, increasing See Increasing events
Event, invariant under transformation 128
Exchange matrix 423
Excursion in Temkin's problem 388
Expected number of clusters per lattice site 207
Face of a plane lattice 144 154 156 168
Finite-size scaling 259 266—267 340
First Brillouin zone 245
First-passage time, dimension 477
First-passage time, mean, related to electrical conduction 473—474
First-passage time, mean, related to mean commute time 475
First-passage time, on square lattice incipient infinite cluster 467
Fisher's Lemma 161
Fixed point, attractive 253
Fixed point, stable 253
Fixed point, unstable 253
FKG inequality See Harris-FKG inequality
Flory-type argument 361
Flow capacity 337
For Bethe lattice cluster size, conditioned on radius 37
Fortuin — Kasteleyn — Swendsen — Wang distribution 279
Fractal dimension 477
Fractal dimension, apparent, of the backbone 296
Fractal dimension, apparent, of the infinite cluster 297
Fractal model of backbone 359
Fractal structure, effective, effect on ant in labyrinth 442
Fractals, prior knowledge assumed 2
Fracton dimension 458
Fractons 458—459
Free energy, application to ant in labyrinth 439
Free energy, continuous differentiability of 204
Free energy, convexity of modified form 204
Free energy, F(p, h) defined 203
Free energy, zero-field E(p)=F(p,0), defined by series 164
Free energy, zero-field E(p)=F(p,0), equals mean number of clusters per lattice site 164
Free energy, zero-field E(p)=F(p,0), for Bethe lattice 205
Fully triangulated lattice, defined 168
Fully triangulated lattice, van den Berg's counter-example 47
Gamma function, defined xxiv
Gap exponents, defined 206
Gap exponents, known equal in two dimensions 213 251
Gap exponents, should be equal 210
Generalized master equation 410
Glauber model 70
Graphical distance 476
Grimmett, Kesten, and Zhang, lemma of 481
Grimmett, Kesten, and Zhang, theorem of 481
Hammersley's inequality for site-bond, percolation 53
Hammersley, John M. 3
Harmonic dimension 444 445 459 462 464 467 481 495
Harris — Fisher theorem 154
Harris — FKG inequality, stated and proved 90
Harris — FKG inequality, used 90—92 124 151 152 155 159 229 230 232 240 241 484
Harris' lemma, for a quadrant 147
Harris' lemma, for the half-plane 148
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



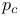 , Bethe lattice
, Bethe lattice 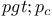 , Bethe lattice
, Bethe lattice 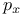 if
if 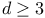
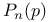 exact for
exact for 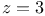 , derivation
, derivation 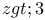 , quoted
, quoted 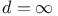
 and
and 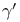 equal
equal 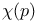
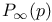
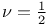
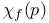
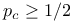
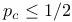
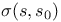
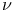 for
for  ,
, 
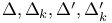
 and
and 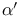
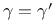
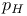 ), defined
), defined  ), defined
), defined 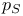 ), defined
), defined