|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hughes B.D. — Random Walks and Random Environments: Random Environments (том 2) |
|
|
 |
| Предметный указатель |
Harris' theorem, generalized by Fisher 153
Harris' theorem, proof of imitated 155 160 162 163
Harris' theorem, stated and proved 149
High-density phase, connectivity function 242
High-density phase, correlation length, defined 243
High-density phase, correlation length, exponent 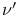 243 243
High-density phase, critical probability ph defined 15
High-density phase, decay of cluster-size distribution 45
High-density phase, defined 15
High-density phase, pair connectedness 242
Hoelder's inequality 219
Honeycomb lattice, dual (triangular lattice) admits Seymour — Welsh theorem 153
Honeycomb lattice, exact bond threshold 142
Honeycomb lattice, exponents same as for triangular 200
Hull, Monte Carlo algorithm for 178
Hull, only part of cluster boundary 300
Hull, used in bounding 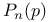 in high-density phase 45 in high-density phase 45
Hyperscaling relations for percolation 207 273
Increasing events, defined 89
Increasing events, Harris — FKG inequality 90
Increasing events, problems with for 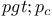 242 242
Increasing events, Russo's Formula 99
Increasing events, van den Berg — Kesten inequality 93
Infimum 15
Infinite cluster, backbone of See Backbone
Infinite cluster, uniqueness of See Uniqueness of infinite cluster
Infinite clusters, mean number is  for Bethe lattice above for Bethe lattice above 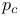 133 133
Infinite clusters, number of is 0, 1 or  133 133
Infinite clusters, number of is well defined 130
Integer part, defined xxiv
Integer part, used 40 96 98 115 237 268 483 487
Integrated density of states 458
Interior boundary 89
Intermediate phase 47
Invariant measures 438
Invasion percolation 63
Jensen's inequality, used 320 328 390 406 412 478
Josephson inequalities 273
Kagome lattice, bounds on bond threshold 170 171
Kagome lattice, can be drawn as modified square lattice 178
Kagome lattice, covering lattice of honeycomb lattice 160
Kagome lattice, site threshold 160
Kelvin — Dirichlet — Wattage lemma 322
Kesten — Golosov theorem 409
Kesten's theorem for myopic ants at 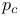 , Bethe lattice 466 , Bethe lattice 466
Kesten's theorem for myopic ants at 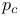 , square lattice 467 , square lattice 467
Kesten's theorem on scaling in two dimensions at the percolation threshold 249
Kesten's theorem on scaling in two dimensions, including approach to the threshold 251
Kesten, Harry 3
Kesten, Kozlov, and Spitzer, theorem of 404
Kinetic Ising model 70
Kirchhoff's law 472
Kirchhoff's law, stated 320
Kirchhoff's law, used 321—324 348 474 475
Landau symbols xix
Laplace transform defined 345 386
Laplace transform defined, used 345—346 400—401 469
Lattice animal expansion, cf. perimeter polynomials 42
Lattice animal expansion, defined 216
Lattice animal expansion, justifying differentiation of series expansions 108 164
Lattice animal expansion, used 38 51 216—228
Lattice animals 216 246 362
Lattice animals, upper critical dimensionality is d=8 362
Lattice trees 246
Lattice, Bethe 245
Lattice, Bethe, backbone probability B(p) 26
Lattice, Bethe, cluster-size distribution 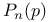 37 37
Lattice, Bethe, defined 22
Lattice, Bethe, Durrett — Nguyen inequality sharp for 216
Lattice, Bethe, exponents  and and 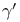 equal 202 equal 202
Lattice, Bethe, exponents summarized 198
Lattice, Bethe, free energy 205
Lattice, Bethe, gelation model 14
Lattice, Bethe, mean cluster size 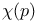 35 35
Lattice, Bethe, percolation probability 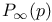 25 25
Lattice, Bethe, percolation threshold of 35
Lattice, Bethe, problems with concavity of F(p, h) 221
Lattice, Bethe, site-bond percolation on 54
Lattice, Bethe, susceptibility 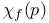 37 37
Lattice, bipartite 56 175 464
Lattice, dense 478
Lattice, dual of 143
Lattice, homogeneous 86
Lattice, honeycomb, bond threshold 142 156
Lattice, honeycomb, dual of triangular 144
Lattice, kagome, bounds on bond threshold 170 171
Lattice, kagome, can be drawn as modified square lattice 178
Lattice, kagome, covering lattice of honeycomb lattice 160
Lattice, kagome, site threshold 160
Lattice, pentagon 170
Lattice, quasicrystalline 181 339
Lattice, smooth 479
Lattice, square, 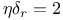 239 239
Lattice, square, 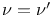 243 243
Lattice, square, 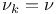 235 235
Lattice, square, bond threshold 142
Lattice, triangular 156
Lattice, triangular, bond threshold 142
Lattice, triangular, site threshold 160
Lattice, “bow-tie” 158 175 200
Lattice, “dice” 170
Law of large numbers, ergodic theory generalizes 127
Law of large numbers, strong form 319 332
Law of large numbers, weak form 319
Left excursion, defined 388
Left excursion, mean duration 397
Left recurrent, defined 388
Left recurrent, necessary and sufficient conditions 388
Lemma, Men'shikov's on coincidence of  and and 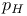 112 112
Lemma, Nguyen's first 235
Lemma, Nguyen's second 236
Lemma, Nguyen's third 237
Lemma, of Chandra et al. 475
Lemma, of Doyle and Snell 473 479
Lemma, of Durrett and Nguyen on concavity of free energy 221
Lemma, of Grimmett, Kesten, and Zhang, proved 486—494
Lemma, of Grimmett, Kesten, and Zhang, stated 481
Lemma, of Men'shikov et al. 115
Lemma, of Nash — Williams 471
Lemma, of Newman on continuity of 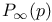 227 227
Lemma, of Oxley and Welsh 20
Lemma, on absence of infinite cluster sites from large box 483
Lemma, on connections between specified sites of large boxes 483
Lemma, on lower bound for 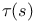 for for  232 232
Lemma, on upper bound for 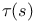 for for  230 230
Lemma, Tasaki's 268
Lemma, “mixing implies ergodic” 129
Long-range percolation 64
Loop currents 331
Low-density phase, bounds on the distribution of the wet set radius 95
Low-density phase, critical probability  defined 33 defined 33
Low-density phase, decay of pair connectedness 97
Low-density phase, decay of the cluster-size distribution 111
Low-density phase, defined 33
Low-density phase, lower bound for mean cluster size 102
Magnetization function, for long-range percolation 67
Magnetization function, for percolation 202
Magnetization function, relevance to ant in labyrinth 495
Mandelbrot, Benoit B. 3
Markov chain 438
Markov chain, formulation of ant in labyrinth 464
Markov chain, Markov process, reversible 443
Markov's inequality, stated and proved 212
Markov's inequality, used 214 413
Master equation, generalized 410
Master equation, with random transition rates 410
Matching lattices 165—168
Matching polynomial 167
Maximum principle, proof set as exercise 325
Maximum principle, used 349 474
| Maxwell, James Clerk 318
Mean cluster size, 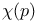 defined 33 defined 33
Mean cluster size, alternative expression 33
Mean cluster size, bounded below 102
Mean cluster size, low-density series for 40
Mean number of clusters per lattice, site 163 439
Mean-field percolation exponents, etymology 199
Mean-field percolation exponents, expected for  246 246
Mean-field percolation exponents, sufficient condition being  199 199
Mean-field percolation exponents, summarized 272
Mean-field percolation exponents, used in Flory-type argument 362
Mean-field percolation exponents, via Potts model 280—281
Measure-preserving transformation 128
Mellin transform 228 416 417
Men'shikov's coincidence lemma, stated and proved 112
Men'shikov's coincidence lemma, used 122
Men'shikov's theorem, proved 114—122
Men'shikov's theorem, stated 112
Men'shikov's theorem, used 152 160 162 218 226
Microscopic conductivity 348
Middle phase 47
Mixing property 129
Mobility 452
Monte Carlo simulation of cluster perimeters or hulls 178—180
Monte Carlo simulation of finite lattices 178
Monte Carlo simulation of single clusters 177—178
Montroll, Elliott W. 3
Mosaic, defined 144
Mosaic, used 153 154
Multifractals 317 360 430 446 505
Myopic ant 438
Neighbourhood of a site 89
Nested inside 472
Newman's lemma on continuity of the percolation probability 227
Nguyen's lemmas 235—237
Nguyen's theorem 234
Node and link model of backbone 358
Node-link-blob model of backbone 360
Non-linear conductance problems 324 332
O(), Landau symbol xix
Ohm's law 472
Ohm's law, stated 320
Ohm's law, used 321 322 324 348 474 475
Onductance 319
Order parameter for long-range percolation 67
Order parameter for percolation 202
Ornstein — Zernike approximation 273 281
Outer boundary of a percolation cluster 300
p-occupied site 107 137
Pair connectedness, at percolation threshold 238—240
Pair connectedness, decay of in low-density phase 97
Pair connectedness, defined 88
Pair connectedness, for Bethe lattice 244
Pair connectedness, in high-density phase 242—244
Pair connectedness, moments of 233
Pair connectedness, scaling theory for 241
Partially oriented percolation 66
Pentagon lattice 170
Percolation See also Percolation theory variations
Percolation conduction problem, defined (bond problem) 333
Percolation conduction problem, effective medium approximation 352—355
Percolation conduction problem, exponent bounds from finite-size scaling 341
Percolation conduction problem, exponent inequalities 335—338
Percolation conduction problem, finite-size scaling 340—342
Percolation conduction problem, likely behaviour 334
Percolation conduction problem, on Bethe lattice, ambiguities in exponent definitions 347—348
Percolation conduction problem, on Bethe lattice, effective medium approximation 347
Percolation conduction problem, on Bethe lattice, exact results 343—347
Percolation conduction problem, on Bethe lattice, potential correlations 348—349
Percolation conduction problem, position-space renormalization 350—352
Percolation conduction problem, renormalized effective medium approximation 356—357
Percolation conduction problem, Sierpinski lattice analogue 349
Percolation conduction problem, Straley's scaling theory 342—343
Percolation conduction problem, variations, continuum problem 339
Percolation conduction problem, variations, site problem 339
Percolation conduction problem, variations, superconductivity problem 338
Percolation of binary words 58
Percolation probability, bounded below 104—107
Percolation probability, continuity of, from left for 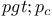 137—138 137—138
Percolation probability, continuity of, from right 137
Percolation probability, continuity of, if  227—228 227—228
Percolation probability, defined 15
Percolation probability, for Bethe lattice 22—26
Percolation probability, high-density series 27—33
Percolation probability, self-avoiding walk bounds 17—19
Percolation theory, bond model See Bond percolation
Percolation theory, contrast with diffusion 4
Percolation theory, counter-examples 47—48
Percolation theory, fundamental problems in, behaviour near threshold 50
Percolation theory, fundamental problems in, locating thresholds 49
Percolation theory, fundamental problems in, structural issues 51—52
Percolation theory, fundamental problems in, threshold problem 46—47
Percolation theory, general references 13—14
Percolation theory, history 4
Percolation theory, notational variation 19
Percolation theory, site model See Site percolation
Percolation theory, variations, AB percolation 55—58
Percolation theory, variations, bipartite percolation 56
Percolation theory, variations, chain percolation 71
Percolation theory, variations, contact process 69—70
Percolation theory, variations, continuum percolation 68—69
Percolation theory, variations, correlated percolation 58
Percolation theory, variations, directed compact percolation 62
Percolation theory, variations, directed percolation 54 59—60 145 187 246 291
Percolation theory, variations, Domany — Kinzel model 60—62
Percolation theory, variations, first-passage percolation 69
Percolation theory, variations, invasion percolation 63—64 184
Percolation theory, variations, long-range models 64—66
Percolation theory, variations, Mandelbrot percolation 70
Percolation theory, variations, mole's labyrinth 71
Percolation theory, variations, multiparameter bond models 69
Percolation theory, variations, partially oriented percolation 66—68
Percolation theory, variations, percolation of coalescing random walks 70
Percolation theory, variations, percolation on quasilattices 70
Percolation theory, variations, polychromatic percolation 54
Percolation theory, variations, site-bond percolation 52—54 187 265
Percolation theory, variations, topologically disordered lattices 58—59
Percolation threshold, bounds 168—171
Percolation threshold, conjectured relation to random walks 172—173
Percolation threshold, conjectures and empirical results 173—175
Percolation threshold, for slice 125
Percolation threshold, known values for d=2 49
Percolation threshold, numerical estimates 175—188
Percolation threshold, of Bethe lattice 35
Percolation threshold, well defined if no middle phase 47
Percolation, bond See Bond percolation
Percolation, site See Site percolation
Perimeter polynomials 40 166
Phonons 458
Picture of a lattice, defined 276
Pivotal site 99
Plaquettes 144
Polya random walk 71
Polychromatic percolation 54
Potts model, correspondence with percolation 277
Potts model, introduced 274
Potts model, mean-field theory 280
Probability space 127
Propagator matrix 424
Proposition of Sykes and Essam 168
q-state Potts model, correspondence with percolation 277
q-state Potts model, introduced 274
q-state Potts model, mean-field theory 280
Quasicrystalline lattice, percolation conduction problem for 339
Quasicrystalline lattice, percolation thresholds 181
Quasilattices 70
Random cluster model 278
Random resistor problem in d dimensions 325—328
Random resistor problem in two dimensions 328—332
Random resistor problem, non-linear 332—333
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



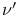
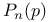 in high-density phase
in high-density phase 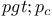
 for Bethe lattice above
for Bethe lattice above 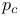
 and
and 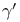 equal
equal 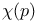
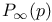
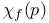
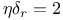
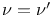
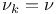
 and
and 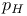
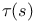 for
for 


