|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Blei R. Ч Analysis in Integer and Fractional Dimensions |
|
|
 |
| ѕредметный указатель |
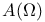 , absolutely convergent W-series 150 , absolutely convergent W-series 150
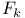 -measures see Frechet measures -measures see Frechet measures
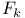 -variation see Frechet variation -variation see Frechet variation
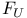 -measure associated with multi-parameter process Chapter XI -measure associated with multi-parameter process Chapter XI 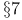
 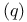 -process 369Ч370 -process 369Ч370
 (symmetric elements in (symmetric elements in 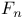 , that vanish on diagonals) 162Ч163 , that vanish on diagonals) 162Ч163
 independent product of 1-integrators Chapter XI independent product of 1-integrators Chapter XI 
 integrator 351Ч353 integrator 351Ч353
 , ,  -chaos 337Ч338 -chaos 337Ч338
 , generalized Wiener process 293Ч294 , generalized Wiener process 293Ч294
 , p-stable motion 373Ч374 , p-stable motion 373Ч374
 , Wiener process 110Ч111 292Ч293 , Wiener process 110Ч111 292Ч293
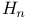 see also nth Wiener Chaos process see also nth Wiener Chaos process
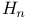 , , 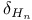 323 323
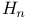 , definition 320 , definition 320
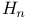 , properties 324 , properties 324
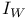 (definition) 290 see (definition) 290 see
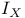 (definition) 358 (definition) 358
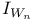 (definition) Chapter X (definition) Chapter X 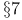 see see
 -bounded additive process 363 381 382 385 387 408 422 30) 423 -bounded additive process 363 381 382 385 387 408 422 30) 423
 -bounded process with orthogonal increments 357 359Ч360 379 388 419 422 -bounded process with orthogonal increments 357 359Ч360 379 388 419 422
 -factorizable 271 276 -factorizable 271 276
 -bounded martingales 363 387 (Exercise -bounded martingales 363 387 (Exercise
 -chaos, construction of exact n-chaos 338 -chaos, construction of exact n-chaos 338
 -chaos, definition 337 364 -chaos, definition 337 364
 -chaos, detection 526 528 -chaos, detection 526 528
 -chaos, for non-integer -chaos, for non-integer  (question) 338 (question) 338
 -chaos, general constructions 420 (Exercise 17) Chapter -chaos, general constructions 420 (Exercise 17) Chapter
 -chaos, homogeneous integrator 364 337 356Ч357 -chaos, homogeneous integrator 364 337 356Ч357
 -chaos, marking randomness 348 -chaos, marking randomness 348
 -chaos, variations of associated F-measures 337 356Ч357 -chaos, variations of associated F-measures 337 356Ч357
 -product, definition 475Ч476 -product, definition 475Ч476
 -product, deterministic constructions Chapter XIII -product, deterministic constructions Chapter XIII 
 -product, random constructions Chapter XIII -product, random constructions Chapter XIII 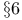
 -system (exact, asymptotic) see also -system (exact, asymptotic) see also  -chaos; -chaos;  -variable; sub- -variable; sub- -variable -variable
 -system (exact, asymptotic), examples 525Ч526 -system (exact, asymptotic), examples 525Ч526
 -variable (exact, asymptotic, standard) see also Sub- -variable (exact, asymptotic, standard) see also Sub- -variable -variable
 -variable (exact, asymptotic, standard) in limit theorems 335 524 -variable (exact, asymptotic, standard) in limit theorems 335 524
 -variable (exact, asymptotic, standard), definition 335 -variable (exact, asymptotic, standard), definition 335
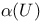 (optimal value of linear programming problem) 478 (optimal value of linear programming problem) 478
 -scale 'continuously' calibrated? 175 434 -scale 'continuously' calibrated? 175 434
 -scale applied to -scale applied to 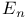 195Ч196 195Ч196
 -scale applied to -scale applied to 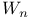 174Ч175 174Ч175
 -scale applied to 3/2-fold Cartesian product Chapter XII -scale applied to 3/2-fold Cartesian product Chapter XII 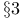
 -scale applied to general fractional Cartesian products Chapter XIII -scale applied to general fractional Cartesian products Chapter XIII 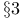
 -scale applied to homogeneous integrator 364 -scale applied to homogeneous integrator 364
 -scale in harmonic analysis setting 174 434 -scale in harmonic analysis setting 174 434
 -scale in probability theory setting Chapter X -scale in probability theory setting Chapter X 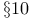
 -scale measuring complexity 175 -scale measuring complexity 175
 -scale measuring interdependence Chapter X -scale measuring interdependence Chapter X 
 -scale, relation to -scale, relation to  -scale 440 500 -scale 440 500
 -scale, relation to dim-scale Chapter XIII -scale, relation to dim-scale Chapter XIII 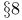
 -measurement see also -measurement see also  -scale -scale
 -measurement in harmonic analysis setting 174 434 -measurement in harmonic analysis setting 174 434
 -measurement in probability theory setting 298 -measurement in probability theory setting 298
 -set problem 56 -set problem 56
 -set union problem 56Ч57 -set union problem 56Ч57
 -space 46 see -space 46 see
 -uniformizability 40 53 54 56Ч57 Chapter Chapter 214 241 -uniformizability 40 53 54 56Ч57 Chapter Chapter 214 241
 -uniformizing constants 210 -uniformizing constants 210
 -uniformizing map 210 -uniformizing map 210
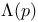 -set definition 55 173Ч174 202 -set definition 55 173Ч174 202
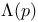 -set problem 56 338 524 -set problem 56 338 524
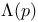 -space 55 58 -space 55 58
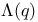 -process, -process, 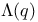 -process and the ' -process and the '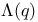 -set problem' 372 -set problem' 372
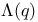 -process, -process, 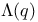 -process and the ' -process and the '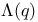 -set problem' for -set problem' for 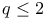 372 372
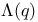 -process, -process, 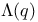 -process and the ' -process and the '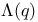 -set problem', constructions 366 (Exercise -set problem', constructions 366 (Exercise
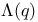 -process, -process, 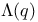 -process and the ' -process and the '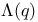 -set problem', definition 366 -set problem', definition 366
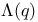 -system 366 -system 366
 (measure associated with (measure associated with  -bounded process) -bounded process)
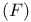 -type see Type -type see Type
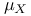 (F-measure associated with process X; definitions) 1-integrator X 351 (F-measure associated with process X; definitions) 1-integrator X 351
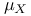 (F-measure associated with process X; definitions) 1-process X 395 530 (F-measure associated with process X; definitions) 1-process X 395 530
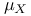 (F-measure associated with process X; definitions), U-integrator X 391 (F-measure associated with process X; definitions), U-integrator X 391
'Theoreme fondamental de la theorie metrique des produits tensoriels' see Grothendieck's 'theoreme fondamental de la theorie metrique des produits tensoriels'
'Zero knowledge' 282 284 330
A(G), absolutely convergent 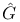 -series 15 -series 15
A(T), absolutely convergent Fourier series 149
Absolutely summing operators: definition 91Ч92
Absolutely summing operators: examples 92
Absolutely summing operators: study by Lindenstrauss and Pelczynski 54 87Ч88
Adaptive stochastic integration 290 317 Chapter 409Ч410
Algebraically independent spectral sets see also Steinhaus system
Algebraically independent spectral sets, definition 191Ч192 436
Algebraically independent spectral sets, example 192 436
Ambient product 458 see
Atomic-molecular hypothesis 280 281
Banach's theorem 53 173
Bimeasures see also Multi-measures
Bimeasures so dubbed 7
Bimeasures, historical connections 9 126Ч129
Bonami's inequalities, general setting 194
Bonami's inequalities, historical context 171Ч174
Bonami's inequalities, measurement of complexity 174Ч175
Bonami's inequalities, statement and proof 170Ч171
Bourgain's theorem 56 338 372 524
Brownian displacements in Einstein s model Chapter X 
Brownian displacements in Wiener's model Chapter X 
Brownian displacements, perceptions 282Ч283
Brownian motion see also Wiener process
Brownian motion in the mathematical literature 306Ч307
Brownian motion, first and further approximations Chapter X 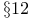
Brownian motion, heuristics leading to models 282Ч285 348
Brownian motion, history 279Ч282
Brownian motion, mathematical model (Wiener's) Chapter X 
Brownian motion, stochastic complexity 338Ч339
Brownian movement see Brownian motion
Brownian particle 282
Brownian sheet 293
Brownian trajectories as random walks 283Ч284 331 336
Brownian trajectories, assumptions about 282 329Ч330
Brownian trajectories, building blocks xiii 73 135 187 191
Brownian trajectories, properties expressed by Wiener process 289Ч290
Burkholder Ч Gundy martingale inequalities 197 (Exercise 11) 299
Caratheodory Ч Hahn Ч Jordan theorem in multidimensional measure theory Chapter VI 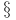 4 4
Carleson's theorem 147
Ceneralized Minkowski inequality 25 32 459
Central limit theorem 284 322 329 330 335 336 343 345
Chaos see  -chaos; homogeneous chaos; Wiener Chaos -chaos; homogeneous chaos; Wiener Chaos
Characteristic function of normal r.v. (in proof of Grothendieck's inequality) 54
Characters of compact Abelian groups 137
Characters, 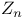 16 (Exercise 4) 34 16 (Exercise 4) 34
Characters,  138Ч139 138Ч139
Characters, 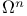 159 159
Circle group 29 55 109 136
Combinatorial complexity of random walks 333Ч334 521 524 528
Combinatorial device 488
Combinatorial dimension see also fractional Cartesian products;  -products -products
Combinatorial dimension in topological and measurable settings Chapter XIV 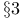
Combinatorial dimension, basic properties 476Ч477
Combinatorial dimension, definition (upper, lower, exact, asymptotic) 475Ч476
Combinatorial dimension, existence of  -dimensional sets 477Ч478 Chapter -dimensional sets 477Ч478 Chapter
Combinatorial dimension, measurement of interdependence 456Ч458 477
Combinatorial dimension, motivation 186Ч188 433Ч434 436
Combinatorial measurements in Walsh system W 493Ч494
Combinatorial-harmonic analytic gauge 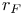 435Ч436 435Ч436
Complete boundedness (relation to LЧfactorisability and convolvability) 271Ч272
complexity see also interdependence; stochastic complexity; combinatorial complexity of random walks
Complexity 'hidden' in drunk's walks 334
Complexity,  -scale 174Ч175 Chapter -scale 174Ч175 Chapter
Complexity,  -scale 188Ч189 -scale 188Ч189
Complexity, evolving in W 137 499Ч500
Continuous geometries 517Ч518
Convolution in 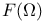 520 520
Convolution in 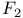 (preview) 78 Chapter (preview) 78 Chapter
Convolution in 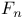 Chapter IX Chapter IX 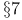
Convolution in 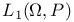 141 141
Convolution in 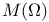 139Ч140 139Ч140
Convolver definition 266
Convolver examples Chapter IX 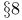
| Cover in definition of fractional Cartesian products 186Ч187 457Ч458
Cover in multilinear Grothendieck inequalities 227Ч228
Cover, k-cover 458
Cover, maximal k-cover 458
Cover, minimal k-cover 493
Crossnorms 81Ч82 see
Cylinder sets 202 (Hint 3) 518
Decision making machines Chapter X  524 see 524 see
Decoupling see also Mazur Ч Orlicz identity
Decoupling in general context 383Ч384
Decoupling in stochastic analysis 382Ч383 384
Dependence (functional) 456Ч457
Difference 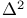 2Ч3 2Ч3
Difference 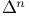 319 319
Differential-space 282 288 330
Diffusion equation 284
DIM see combinatorial dimension
DIMENSION see also Combinatoral dimension; Hausdorfr dimension
Dimension in continuous geometries 517Ч518
Dimension in diverse contexts 517
Dimension index of interdependence 427Ч428
Dimension of 1-process 395 530Ч531
Direct products 86Ч87 see
Dissociate sets in  191Ч192 191Ч192
Dissociate sets in  and W 185 and W 185
Dot product see also Inner product in Grothendieck's inequality
Dot product, alternative representation 40 43 45Ч46 51
Dot product, Grothendieck's representation 54Ч55
Drunk's walk 331Ч333 see
Drury's theorem 190
Dual group see Characters
Elementary tensors see also Building blocks
Elementary tensors as characters 159
Elementary tensors as products of 'building blocks' 73 135
Elementary tensors, definition 72 80
Elementary tensors, elementary U-tensors 442 450 506
Entropy in sense of Shannon 285
Entropy metric 190
Factorization see also Grothendieck factorization theorem;  -factorizable; Pietsch factorization theorem -factorizable; Pietsch factorization theorem
Factorization of linear maps 98
Factorization of multilinear functional 103Ч105 105
Finite Fourier transform 7 see
Fourier Ч Stieltjes series 136 see
Fourier Ч Wiener series 294 see stochastic
Fractional Cartesian products see also  -products -products
Fractional Cartesian products in dimension 3/2 448
Fractional Cartesian products, definition 457Ч458
Fractional Cartesian products, preview 186Ч187 226Ч227
Fractional sum 465
Frechet measures definition (in integer dimensions) 107
Frechet measures in fractional dimensions Chapter XII  Chapter Chapter
Frechet measures in harmonic analysis Chapter XIV 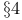
Frechet variation (definition) see also Tensor norms; variation
Frechet variation in fractional-dimensional setting 449 504
Frechet variation of function in one variable 515
Frechet variation of function in two variable 2Ч3
Frechet variation of product F-measures 255
Frechet variation of two-dimensional array 4 23
Frechet variation, 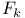 -variation in multidimensional measurable setting 111Ч112 -variation in multidimensional measurable setting 111Ч112
Frechet variation, 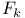 -variation in primal setting 60 -variation in primal setting 60
Frechet variation, 3/2-linear version 14
Frechet's theorem see also multilinear Riesz representation theorem
Frechet's theorem, general measurable version 123
Frechet's theorem, original statement 3
Frechet's theorem, simplest multidimensional version 10
Fubini-type property, statement 67Ч68
Fubini-type property, verified by Littlewood 72
Functional independence see also Independence
Functional independence of generalized Rademacher systems 28
Functional independence of Rademacher system 20 139 189
Functional independence, 'almost functional' independence 189
Functional independence, 1-Sidonicity 188Ч189
Functional independence, definition 187Ч188
Gauss matrix see also finite Fourier transform
Gauss matrix , isometry 28
Gauss matrix in 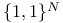 179Ч181 258 179Ч181 258
Gauss matrix, extremal property 62
Gauss matrix, three-dimentional version 62
Gaussian distributions in Brownian movement in Einstein's model 280 284 330Ч331
Gaussian distributions in Brownian movement in Wiener's model 285Ч286 330Ч331
Gaussian distributions in Brownian movement, consequence of maximum entropy 285
Gaussian distributions in Brownian movement, simple random walk model 283Ч284
Gaussiona series 300-301 342(Exercise
Generating set 153
Gliding hump argument 72 93
Grandmasters 137 300
Grothendieck factorization theorem see also Pietsch factorization theorem
Grothendieck factorization theorem in proof that every 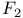 -measure is protectively bounded 257 -measure is protectively bounded 257
Grothendieck factorization theorem in stochastic integration 379 Chapter
Grothendieck factorization theorem, equivalent to Grothendieck's inequality Chapter V 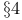 206Ч208 206Ч208
Grothendieck factorization theorem, multilinear extensions Chapter V 
Grothendieck factorization theorem, statement and proof 9 96Ч97
Grothendieck inequality see also multilinear Grothendieck inequality
Grothendieck inequality in proof of Grothendieck factorization theorem 97
Grothendieck inequality in proof that convolution is feasible 78 98Ч100
Grothendieck inequality in proof that every 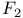 -measure is protectively bounded 257 -measure is protectively bounded 257
Grothendieck inequality, concise statement 39
Grothendieck inequality, constant in inequality 55 83
Grothendieck inequality, constructive proof 49
Grothendieck inequality, crucial step in 'self-contained' proofs 45
Grothendieck inequality, derivation from the Khintchin  - - inequality (problem) 40 inequality (problem) 40
Grothendieck inequality, dual formulation 80 84Ч85
Grothendieck inequality, equivalent to  -uniformizability (problem) 54 -uniformizability (problem) 54
Grothendieck inequality, equivalent to Grothendieck factorization theorem Chapter V 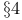
Grothendieck inequality, extending to  17 (Exercise 6) 17 (Exercise 6)
Grothendieck inequality, extending to higher dimensions (problem) 13 88
Grothendieck inequality, formulation by Lindenstrauss and Pelczynski 8 38 87 206
Grothendieck inequality, generalization of Littlewood's mixed-norm inequality 7 11 17
Grothendieck inequality, Grothendieck's original formulation and proof 54Ч55 58 80
Grothendieck inequality, multilinear extensions Chapter VIII
Grothendieck inequality, proofs based on  -uniformizability Chapter III -uniformizability Chapter III
Grothendieck inequality, restatements 8Ч9 38Ч39 80 83 92 206 272
Grothendieck inequality, theoreme fondamental 8 9 38 45 54 88
Grothendieck inequality, two-dimensional surprise 61
Grothendieck measure of Wiener product process 404
Grothendieck measure, definition 385
Grothendieck measure, examples 387 422
Grothendieck measure, products 399
Grothendieck's 'theoreme rondamental de la theorie metrique des produits tensoriels' 8 9 38 45 54 88
Grothendieck's 'theoreme rondamental de la theorie metrique des produits tensoriels', essence 45
Grothendieck's 'theoreme rondamental de la theorie metrique des produits tensoriels', milestone 8Ч9 38 54
Grothendieck's 'theoreme rondamental de la theorie metrique des produits tensoriels', two-dimensional statement 88
Grothendieck-type inequalities see also multilinear Grothendieck inequalities; protectively bounded Frechet measures; projectively bounded forms
Grothendieck-type inequalities in fractional dimensions 453 510
Grothendieck-type inequalities, expressed by protective boundedness 13Ч14 Chapter
Grothendieck-type inequalities, linked to product F-measures Chapter IX  451Ч452 451Ч452
Grothendieck-type inequalities, trilinear 11 225Ч226 429
Haar measure on 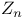 16 (Exercise 4) 34 16 (Exercise 4) 34
Haar measure on  140Ч141 140Ч141
Haar measure on locally compact Abelian groups 137
Haar Ч Wiener series 342 (Exercise 13 ii) see
Hadamard sets 150
Hausdorff dimension 517 see
Hidden variables Chapter X  521 see 521 see
Hilbert inequality (use by Littlewood) 6 15 62
Homogeneous chaos 311 348 see Wiener
Homogeneous integrator 362
Incidence 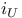 (definition) 468 (definition) 468
Indefinite stochastic integral 354 419
Independence see also Functional independence interdependence
Independence in basic context 456Ч457
Independence in Einstein's model of Brownian motion 284 329Ч330
Independence in Wiener's model of Brownian motion 285Ч286 330Ч331
Independence, algebraic 191Ч192 436
Independence, conveyed by sub-Gaussian system 297Ч299
Independence, functional 188
Independence, heuristic sense 329
Independence, philosophical 'exercise' 342 (Exercise 14)
Independence, statistical xvii
Independence, three notions of independence 299Ч300
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



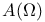 , absolutely convergent W-series
, absolutely convergent W-series 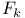 -measures
-measures 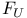 -measure associated with multi-parameter process
-measure associated with multi-parameter process 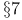

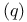 -process
-process 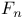 , that vanish on diagonals)
, that vanish on diagonals) 
 -chaos
-chaos 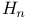
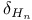
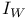 (definition)
(definition) 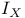 (definition)
(definition) 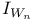 (definition)
(definition)  -bounded additive process
-bounded additive process  -bounded process with orthogonal increments
-bounded process with orthogonal increments  -bounded martingales
-bounded martingales 
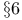
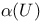 (optimal value of linear programming problem)
(optimal value of linear programming problem)  -scale 'continuously' calibrated?
-scale 'continuously' calibrated? 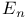
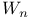
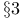
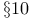
 -scale
-scale 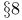
 -measurement
-measurement  -set problem
-set problem 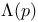 -set definition
-set definition 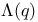 -process,
-process, 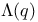 -process and the '
-process and the '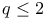

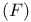 -type
-type 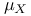 (F-measure associated with process X; definitions) 1-integrator X
(F-measure associated with process X; definitions) 1-integrator X 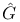 -series
-series 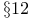

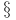 4
4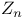

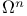
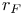
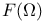
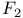 (preview)
(preview) 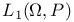
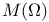

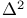
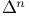

 and W
and W 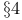
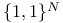
 -
- inequality (problem)
inequality (problem) 
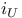 (definition)
(definition)