|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Blei R. — Analysis in Integer and Fractional Dimensions |
|
|
 |
| Предметный указатель |
Independent products of integrators Chapter XI 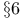
Injective tensor norm 60 82 see
Inner product in Grothendieck's inequality 9 13 17 see
Integral with respect to integrator see also Adaptive stochastic integration
Integral with respect to integrator, 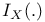 (functional-analytic approach) 351 (functional-analytic approach) 351
Integral with respect to integrator, ![$\int_{[0,1]}dX$](/math_tex/24f40fe75182082cbb4eb52c4cbd747d82.gif) (measure-theoretic approach) 353 (measure-theoretic approach) 353
Integral with respect to integrator, multi-parameter case (preview) Chapter XI 
Integration by parts formula 411
Integration with respect to 'n—dimensional' 1-process 396
Integration with respect to Frechet measures Chapter VI  122 130—132 506—507 122 130—132 506—507
Integrator Chapter XI  Chapter Chapter
Interchange of limit and integration 417
Interdependence see also Complexity
Interdependence as complexity 187—188
Interdependence in random walks Chapter X 
Interdependence of elementary tensors 186—187
Interdependence, conveyed by tail-probabilities 297—299 Chapter 364
Interdependence, functional 175
Interdependence, marked by 'dimension' Chapter XII  Chapter Chapter
Interdependence, marked by 'type' 444—447
Interdependence, marked by combinatorial dimension 477—478 517
Interdependence, marked by dimension of 1-process 503 530—531
Interdependence, measurements 187
Interdependence, statistical 175
Iterated integral Ito integral 316—317
Iterated integral with respect to Frechet measure 120
Iterated integral with respect to n-process 379
Iterated integral with respect to product Frechet measures 263—264
Iterated integral, Lebesgue — Stieltjes 131—132 (Exercises 15 16)
Iterated integral, Riemann—Stieltjes 3
Ito integral: as iterated integral Chapter X 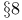
Ito integral: via measure-theoretic approach 405—408
Ito's formula 318 343 409
k-disjoint rectangles 63
Kahane — Salem — Zygmund estimates 301
Khintchin 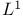 - -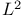 inequality see also inequality see also  -set problem Chapter -set problem Chapter
Khintchin 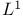 - -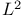 inequality for general systems 30 inequality for general systems 30
Khintchin 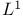 - -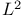 inequality in dimension n 202 (Exercise 32) inequality in dimension n 202 (Exercise 32)
Khintchin 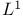 - -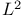 inequality, equivalence to Littlewood's and Orlicz's mixed-norm inequalities Chapter II inequality, equivalence to Littlewood's and Orlicz's mixed-norm inequalities Chapter II 
Khintchin 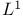 - -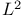 inequality, history 22—23 inequality, history 22—23
Khintchin 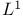 - -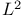 inequality, statement, proof, and history Chapter II inequality, statement, proof, and history Chapter II 
Khintchin 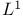 - -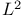 inequality, upgraded 40 46 see inequality, upgraded 40 46 see
Khintchin inequalities in dimension 3/2 Chapter XII 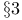
Khintchin inequalities in fractional dimensions Chapter XIII 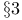
Khintchin inequalities, application to  -uniformizing constants 49 -uniformizing constants 49
Khintchin inequalities, history and impact 22 55 171—174
Khintchin inequalities, proofs 32 (Exercise 3) 342
Kronecker product 249
Lacunary 12 53 150 173 185 189 191 198 199 424
Law of the iterated logarithm 22 171—172
Limit theorems 335 338 521—522
Linear programming problem (associated with a fractional Cartesian product) 478
Littlewood 2n/(n+1)-inequality, an extension of Littlewood's 4/3-inequality 10—11
Littlewood 2n/(n+1)-inequality, application in harmonic analysis 185
Littlewood 2n/(n+1)-inequality, application in tensor analysis 185—186
Littlewood 2n/(n+1)-inequality, calibrating Plancherel's theorem 187
Littlewood 2n/(n+1)-inequality, marking functional interdependence 175 188—189
Littlewood 2n/(n+1)-inequality, statement and proof Chapter VII 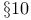
Littlewood index I (of):  -chaos 364 -chaos 364
Littlewood index I (of): 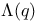 -process 369 -process 369
Littlewood index I (of): 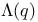 -process 372 -process 372
Littlewood index I (of): 1-integrator 356
Littlewood index I (of): F-measure 507
Littlewood index I (of): nth Wiener chaos process 325
Littlewood index I (of): p-stable motion 374
Littlewood index I (of): U-integrator 392 528—529
Littlewood index I (of): Wiener process 307 310
Littlewood inequality in dimension 3/2 application to tensor products 443
Littlewood inequality in dimension 3/2 application to tensor products, preview 185—187
Littlewood inequality in dimension 3/2 application to tensor products, statement and proof Chapter XII 
Littlewood inequality in fractional key in observing 'd-dimensional' 1—processes 531
Littlewood inequality in fractional key in observing 'd-dimensional' 1—processes, statement and proof Chapter XIII 
Littlewood mixed-norm inequality see also Orlicz's mixed-norm inequality
Littlewood mixed-norm inequality in Orlicz's paper 33 (Exercise 5)
Littlewood mixed-norm inequality in stochastic setting 371
Littlewood mixed-norm inequality, equivalence to Khintchin 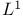 - -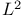 and Orlicz's mixed-norm inequalities Chapter II and Orlicz's mixed-norm inequalities Chapter II 
Littlewood mixed-norm inequality, extensions 176 463—464 489
Littlewood mixed-norm inequality, feasibility of extension 17 (Exercise 6)
Littlewood mixed-norm inequality, precursor to and instance of Grothendieck's inequality 7 11 17 39—40
Littlewood mixed-norm inequality, reformulation 92 (Exercise 19 i)
Littlewood mixed-norm inequality, statement and proof 23—24
Littlewood mixed-norm inequality, use by Davie 11
Littlewood's 4/3-inequality, answer to question by Daniell 6—7
Littlewood's 4/3-inequality, application in harmonic analysis 178 185
Littlewood's 4/3-inequality, application in tensor analysis 62
Littlewood's 4/3-inequality, statement and proof Chapter II 
Lower combinatorial dimension 476
m-linear Hoelder inequality 458—459
Martingales 146 196—197 see
Maximal cover (definition) 458
Maximal fractional Cartesian product (definition) 493 see
Mazur — Orlicz identity 163 383 see
Measure-theoretic approach (to stochastic integration) deterministic integrands 351
Measure-theoretic approach (to stochastic integration), Ito integral 405
Measure-theoretic approach (to stochastic integration), multi-parameter case 379 380
Measure-theoretic approach (to stochastic integration), p-stable motion 373
Measure-theoretic approach (to stochastic integration), via stochastic series 412
Minimal fractional Cartesian product (definition) 493
Mixed-norm inequalities see Littlewood's mixed norm inequalities; Orlicz's mixed-norm inequalities
Mixed-norm space (in Grothendieck inequality) 51 251
Multi-measures 83 see
Multidimensional integral 379
Multilinear Grothendieck inequalities Chapter VIII see
Multilinear Riesz representation theorem Chapter VI  see see
Multiple Wiener integral Chapter X  see see
Multiple Wiener — Ito integral 311
n-disjoint 485
n-process 343 (Exercise 28)
Nikodym boundedness principle 112 129
Non-adapted stochastic integrals 410
Non-anticipative stochastic normalization 331
Nowhere differentiability of sample paths of Wiener process 289
nth Wiener Chaos process 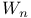 Chapter X Chapter X 
nth Wiener Chaos process 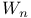 , associated , associated 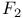 -measure -measure 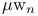 325 325
nth Wiener Chaos process 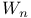 , definition 325 , definition 325
nth Wiener Chaos process 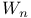 , stochastic complexity of , stochastic complexity of 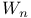 328 328
nth-Wiener chaos Chapter X  338 338
Ogawa integral 418
Optimal 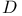 -type see Type -type see Type
Optimal 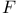 -type see Type -type see Type
Orlicz functions 297 307—308 321
Orlicz norms (marking stochastic complexity) 311 328—329
Orlicz's mixed-norm inequality, equivalence to Khintchin 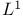 - -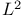 and Littlewood's mixed-norm inequalities Chapter II and Littlewood's mixed-norm inequalities Chapter II 
Orlicz's mixed-norm inequality, in stochastic setting 369—370
Orlicz's mixed-norm inequality, multilinear extension 176
Orlicz's mixed-norm inequality, reformulation 92 (Exercise 19 iv)
Orlicz's mixed-norm inequality, statement, proof, and history 24—25 33
p-Sidon set see also Sidon set
p-Sidon set in 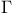 466—467 466—467
p-Sidon set in W 465—466
p-Sidon set, basic characterizations 182
p-Sidon set, combinatorial characterization problem 190
p-Sidon set, definition (exact, asymptotic) 182
p-Sidon set, existence problem (p-Sidon set problem) 13 189 428
p-Sidon set, finite union problem 190
p-Sidon set, historical comments 185
p-Sidon set, terminology 182
p-stable motion, definition 373
p-stable motion, integrator 373
p-stable motion, physical meaning 378—379
p-stable motion, properties 374
p-stable motion, variations of associated 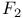 -measure 374—378 -measure 374—378
p-variation see also Littlewood index
p-variation of Frechet measures 128 507
p-variation of scalar functions on [0,1] 515
Paley ordering of Walsh system 146 196—197
Parseval's formula 16 (Exercise 4) 142
Pietsch factorization theorem 98 101 105
Pisier's theorem 173 190
Plancherel's theorem in 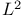 ( (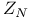 , uniform measure) 16 (Exercise 4) , uniform measure) 16 (Exercise 4)
| Plancherel's theorem in 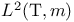 196 (Exercise 1) 196 (Exercise 1)
Plancherel's theorem in 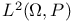 144—145 144—145
Plancherel's theorem, calibration 187
Polarization identities 163 167 200 421 see
Product Frechet measure in dimension 3/2 Chapter XII 
Product Frechet measure in fractional dimensions 509—510
Product Frechet measure in stochastic setting 399
Product Frechet measure, definition 248
Product Frechet measure, link with Grothendieck-type inequalities 254
Products of  -bounded additive processes 408—409 -bounded additive processes 408—409
Products of Wiener processes 402—408
Projective tensor algebra Chapter IV  Chapter 130 186 Chapter 130 186
Projective tensor norm 61 81 82 87 121 260—261 see
Projective tensor product see projective tensor algedra
Projectively unbounded F-measures Chapter IX  see see
Projectively unbounded functionals Chapter VIII  see see
Protectively bounded forms see also Grothendieck-type inequalities
Protectively bounded forms, characterizations 208—209 Chapter 230
Protectively bounded forms, definition 13—14 208
Protectively bounded forms, general characterization (problem) 240—242
Protectively bounded Frechet measures see also Grothendieck-type inequalities; product Frechet-measure; Protectively bounded forms
Protectively bounded Frechet measures in dimension 3/2 Chapter XII 
Protectively bounded Frechet measures in fractional dimensions 509—512
Protectively bounded Frechet measures in topological setting Chapter IX 
Protectively bounded Frechet measures in topological-group setting Chapter IX 
Protectively bounded Frechet measures, characterization 254
Protectively bounded Frechet measures, definition 253
Quadratic variation 290 317 340
Rademacher characters 146 see
Rademacher functions see also Rademacher system
Rademacher functions, characters on  137 137
Rademacher functions, definition 2 19 146
Rademacher functions, statistically independent random variables 20—21
Rademacher series 53
Rademacher system see also Rademacher functions
Rademacher system, definition 2 19
Rademacher system, generalizations Chapter II  191 191
Rademacher system, independent system 20—21 139
Rademacher system, sub-Gaussian system 299
Random integrands Chapter XI 
Random integrator 356
Random series 200—201 (Exercise 30) Chapter
Random walks see also Simple random walks; Decision making machines
Random walks by drunks Chapter X 
Random walks, F-walks 333—335 336 Chapter
Random walks, simplest model of Brownian motion 283—284 331
Randomness 281 311 348 355—357 361—362
Reduced fractional Cartesian products 493
Restriction algebras 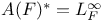 158 158
Restriction algebras 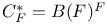 158 158
Restriction algebras 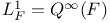 245 (Hint 4) 245 (Hint 4)
Restriction algebras (duals and preduals) see also tensor representations of restriction algebras
Restriction algebras A(F) 158
Restriction algebras B(F) 157
Restriction algebras in harmonic analysis Chapter VII 
Restriction algebras in harmonic and tensor analysis Chapter VII 
Restriction algebras V_n|_F 163
Riemann — Lebesgue lemma 145
Riesz product 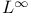 -version 53—54 173 203 -version 53—54 173 203
Riesz product, construction 198—199 (Exercises 17 18)
Riesz product, expansion 144 192—193
Riesz product, first appearance 53
Riesz product, summability kernel 143—144
Riesz representation theorem in dimension 3/2 451 454
Riesz representation theorem in fractional dimensions 507
Riesz representation theorem, measure-theoretic version 1
Riesz representation theorem, multilinear form 126
Riesz representation theorem, original form 1
Riesz representation theorem, primal form 1—2 72
Riesz set 200 (Exercise 26)
Riesz's (M.) theorem 147 197
Rosenthal property 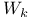 Chapter VII Chapter VII 
Rosenthal property in general setting 194
Rosenthal property, equivalent to separability 166 199
Rosenthal property, products of Sidon sets 72
Rosenthal set 151 see
Sample-path continuity of  -chaos 366 -chaos 366
Sample-path continuity of 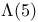 -process 368 -process 368
Sample-path continuity of Wiener process 305
Sample-path continuity via stochastic series, entropy, majorizing measures and Kolmogorov's theorem 368
Scales (relations between) 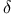 -scale and -scale and 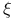 -scale (problem) 500 -scale (problem) 500
Scales (relations between)  -scale and -scale and 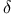 -scale (problem) 500 -scale (problem) 500
Scales (relations between) dim-scale and 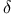 -scale Chapter XIII -scale Chapter XIII 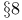
Scales (relations between) dim-scale and  -scale Chapter XIII -scale Chapter XIII 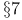
Schur product 272 (Exercise 2)
Schur property of 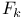 69—72 69—72
Schur property of Sidon space 89 (Exercise 8)
Schur property, definition 69
Schur's theorem 69
Semi-martingale 409
Series, Fourier — Stieltjes series 136
Series, Fourier — Wiener series 294
Series, Haar — Wiener series 341—342 (Exercise 13)
Series, stochastic series approach to integration 412—419
Series, stochastic series approach to sample-path continuity 368
Series, stochastic series of a Wiener process 294—295 341
Series, stochastic series of integrator 387
Series, W-series 140
Series, Walsh series 147
Series, Walsh — Wiener series 341—342 (Exercise 13)
Sidon see also p-Sidon set; Pisier's theorem
Sidon exponent 12 182 428
Sidon sequence 89 (Exercise 8)
Sidon set (definition) 12 145 150
Sidon set is sub-Gaussian 300
Sidon space 89 (Exercise 8)
Sidon, combinatorial characterization of Sidon sets 190
Sidon, finite union of Sidon sets 190
Sidon, Sidon's theorem 12 150
Sidon, Sidonicity and functional independence 188—189
Simple random walk see also Random walks
Simple random walk by drunk 331
Simple random walk, approximation to Brownian movement 283—284 329
Simple random walk, instance of F-walks 333
Skorohod integral 417—418
Spectrum 145
Standard  -variable 335 524 see -variable 335 524 see
Standard step function 312
Standard Sub- -variable 522 see -variable 522 see
Steinhaus functions in Littlewood's work 22 172
Steinhaus functions, definition 30
Steinhaus functions, dubbed by Salem and Zygmund 30 172 300
Steinhaus functions, independent characters 192 436
Steinhaus functions, involving inequalities equivalent to Khintchin's 172 195
Steinhaus system see Steinhaus functions
Stochastic complexity in 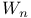 328—329 328—329
Stochastic complexity measurements Chapter X 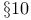
Stochastic complexity of  -chaos 348 364 -chaos 348 364
Stochastic complexity of Brownian displacements 348
Stochastic complexity of random walks 333—334 522
Stochastic complexity, conveyed by variations of F-measures 355—357
Stochastic complexity, detecting complexity of Brownian movement 338—339
Stochastic complexity, Wiener process is least complex 311 328 357
Stone Cech compactification 93 (Hint 12)
Stratonovich integral 407 416
Strongly disjoint sets 153
Sub- -system 321 see -system 321 see
Sub- -variable 321 see -variable 321 see
Sub-Gaussian systems Chapter X 
Summability kernel 142
Sup-norm partition 467
Superior integral 128—129 133
Symmetric functions that vanish on the 'hyper-diagonals' 313
Symmetric functions that vanish on the diagonal 312
Symmetric n-arrays 162
Symmetrization in ![$[0,1]^2$](/math_tex/e6d8e6aa80e37911f6bf1dcf9895436082.gif) 312 312
Symmetrization in ![$[0,1]^n$](/math_tex/b722b050ffe3cb05370cd93d4d9ce80782.gif) 314 314
Symmetrization, role in stochastic integration 315—316
Tail-probabilities see also Complexity; Stochastic complexity; Interdependence
Tail-probabilities, exponential estimates 363—364 524
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



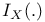 (functional-analytic approach)
(functional-analytic approach) ![$\int_{[0,1]}dX$](/math_tex/24f40fe75182082cbb4eb52c4cbd747d82.gif) (measure-theoretic approach)
(measure-theoretic approach) 


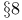
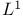 -
-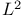 inequality
inequality  -set problem
-set problem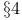

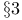
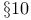
 -chaos
-chaos 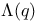 -process
-process 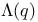 -process
-process 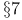
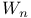

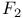 -measure
-measure 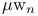
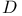 -type
-type 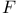 -type
-type 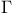
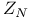 , uniform measure)
, uniform measure) 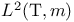
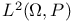
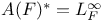
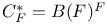
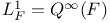
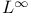 -version
-version 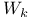
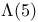 -process
-process 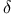 -scale and
-scale and 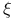 -scale (problem)
-scale (problem)  -scale and
-scale and 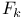
![$[0,1]^2$](/math_tex/e6d8e6aa80e37911f6bf1dcf9895436082.gif)
![$[0,1]^n$](/math_tex/b722b050ffe3cb05370cd93d4d9ce80782.gif)