|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Blei R. — Analysis in Integer and Fractional Dimensions |
|
|
 |
| Предметный указатель |
Tail-probabilities, gauge (scale) of interdependence 297—299 320 363—364
Tail-probabilities, measuring independence 295 297—298
Tail-probabilities, polynomial estimates 364 524
Tensor norms (definitions) 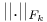 (instance of injective tensor norm) 60 (instance of injective tensor norm) 60
Tensor norms (definitions) 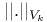 (instance of protective tensor norm) 82 (instance of protective tensor norm) 82
Tensor norms (definitions) 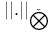 (injective tensor norm) 82 (injective tensor norm) 82
Tensor norms (definitions) 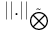 (proactive tensor norm) 82 (proactive tensor norm) 82
Tensor norms (definitions), g-norms 39 85—86
Tensor norms (definitions), greatest and least crossnorms 82
Tensor product (definitions) in dimension 3/2 Chapter XII 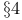
Tensor product (definitions) in fractional dimension 467—469
Tensor product (definitions), algebraic 72—73 81
Tensor product (definitions), injective 82
Tensor product (definitions), projective 81
Tensor representations of restriction algebras see also restriction algebras; tensor products; tensor norms
Tensor representations of restriction algebras in general setting 193—194
Tensor representations of restriction algebras, 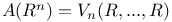 161 161
Tensor representations of restriction algebras, 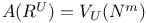 237 237
Tensor representations of restriction algebras, 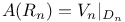 163 163
Tensor representations of restriction algebras, 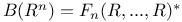 161 161
Tensor representations of restriction algebras, $B(R^n)=\tilde{V}_n(R,...,R) 167
Tensor representations of restriction algebras, 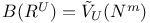 237—238 237—238
Tensor representations of restriction algebras, 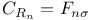 163 167 163 167
Tilde algebra 79—80 see
Time homogeneity (assumption in Brownian movement) 282—283 330
Time-directions 445
Time-independence 350 394
Time-inhomogeneity 523
Time-sequence dependence 396 444—447
Transforms 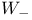 141 141
Transforms of 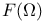 -measures 520 -measures 520
Transforms of 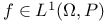 141 141
Transforms of 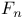 -measure 264 -measure 264
Transforms of convolution of 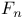 -measures 266 -measures 266
Transforms, Fourier 196 (Exercise 1)
Transforms, Fourier — Stieltjes 136
True F-measures 108 508 509 514 520
Truncation argument (in proof of Grothendieck's inequality) 49
Type 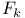 63 186 340—341 63 186 340—341
Type 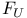 and and 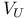 443—447 512—515 519 443—447 512—515 519
Type 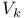 78 186 78 186
Type, optimal 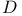 -type 515 -type 515
| Type, optimal 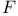 -type 514 530 -type 514 530
Uniformizable  -set (definition) 210 -set (definition) 210
Uniformizable  -space (definition) 46 -space (definition) 46
Uniformly incident cover 470
Variation see also Frechet variation; p-variation; Quadratic variation
Variation in sense of Prechet 2—3 126
Variation in sense of Vitali 2 127
Variation, total variation of measure 112
von-Neumann inequality 11
W-polynomials 141
Walsh characters 146
Walsh functions 146
Walsh series see Series
Walsh system character group of  146 146
Walsh system of continuously increasing index 499—500
Walsh system of integer order 147—148
Walsh system of non-integer order (preview) 175
Walsh — Wiener series see series
White noise, associated with  -additive process 422 (Exercise 30 ii) -additive process 422 (Exercise 30 ii)
White noise, associated with a product of Wiener processes 405
White noise, associated with integrator 355 358 394
White noise, associated with p-stable motion 422 (Exercise 30 i)
White noise, associated with Wiener process 111 202—203
White noise, n-dimensional (question) 319
Wiener 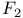 -measure: definition 110—111 292 -measure: definition 110—111 292
Wiener 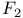 -measure: generalized 293—294 -measure: generalized 293—294
Wiener 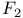 -measure: variations Chapter X -measure: variations Chapter X 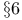
Wiener Chaos see also nth Wiener Chaos process
Wiener Chaos of order n 320
Wiener Chaos, decomposition 320
Wiener integral, definition 290
Wiener integral, generalization 358—359
Wiener measure 288
Wiener process, constructions 286—288
Wiener process, definition 285—286
Wiener process, generalized 293—294
Wiener process, least complex model 311
Wiener process, limit of simple random walks 283—284 329
Wiener process, preview 17—18 (Exercise 8)
Wiener process, series representation 294—295
Wiener process, Wiener's first approximation to Brownian movement 329
Wiener space 287—288
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



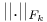 (instance of injective tensor norm)
(instance of injective tensor norm) 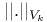 (instance of protective tensor norm)
(instance of protective tensor norm) 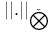 (injective tensor norm)
(injective tensor norm) 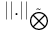 (proactive tensor norm)
(proactive tensor norm) 
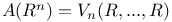
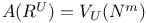
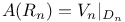
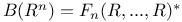
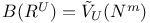
 -measures
-measures 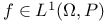
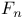 -measure
-measure 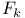
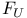 and
and 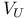
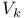
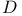 -type
-type 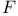 -type
-type  -set (definition)
-set (definition) 
 -additive process
-additive process  -measure: definition
-measure: definition