Авторизация
Поиск по указателям
Fraisse R. — Theory of Relations
Обсудите книгу на научном форуме Нашли опечатку?
Название: Theory of RelationsАвтор: Fraisse R. Аннотация: Relation theory originates with Hausdorff (Mengenlehre 1914) and Sierpinski (Nombres transfinis, 1928) with the study of order types, specially among chains = total orders = linear orders. One of its first important problems was partially solved by Dushnik, Miller 1940 who, starting from the chain of reals, obtained an infinite strictly decreasing sequence of chains (of continuum power) with respect to embeddability. In 1948 I conjectured that every strictly decreasing sequence of denumerable chains is finite. This was affirmatively proved by Laver (1968), in the more general case of denumerable unions of scattered chains (ie: which do not embed the chain Q of rationals), by using the barrier and the better orderin gof Nash-Williams (1965 to 68).
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2000Количество страниц: 456Добавлена в каталог: 19.11.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Extensive subset, relatively extensive subset 12.7.1 Extensivity, poset of height two 8.5.2 Extensivity, tableau 8.4 Exterval 9.8.1 Extracted sequence 1.2.2 Extraction property 4.11.3 Extraction theorem for well partial orderings 4.5.1 Faithful augmentation 8.6 Faithful extension, bivalent tableau 8.4 Faithful extension, chain 8.2 Faithful extension, relation 8.1 FEFERMAN, dependent choice and choice for finite sets 1.8 FELGNER, augmentation and ultrafilter axioms 2.9.3 Filter, finer filter 2.3.1 Final interval 2.2.1 Finite set, Dedekind 1.1.4 Finite set, Tarski 1.1.1 Finitely bounded relation or age 13.1.2 13.2.3 Finitely free poset 4.3.1 Finitist relation 10.8 Finitist relation, finitist structure 10.11.1 Fixed point lemma (Knaster) 1.1.3 FOLKMAN, Ramsey numbers 3.1.6 Forb( A.2.4 Forerunner barrier 7.3.1 Forerunner barrier, forerunner barrier sequence 7.3.3 Foundation axiom 1.2 Foundation axiom, consistency 1.9.1 Foundation axiom, scheme of foundation 1.2.7 FRAENKEL, domain and range 1.1.8 10.11.1 FRAENKEL, proof of Bernstein — Schroeder 1.1.5 FRAENKEL, substitution scheme and axioms of ZF 1.2.4 Fragil family 11.5.1 Fragil family, morphism 11.6 Fragil family, relation 11.5.3 FRAIESSE 2.14 5.10.4 8.5.2 FRAIESSE, back-and-forth 10.10 FRAIESSE, characterization of finitist relations 10.9.8 FRAIESSE, Fraenkel — Mostowski model 10.11.1 FRAIESSE, interval-filter and interval-closure 11.7 FRAIESSE, relational or strong interval 9.8 FRASNAY, bounds of a chainable relation 13.2.3 FRASNAY, chainability theorem 13.3.3 FRASNAY, degree of a universal class 13.12.2 FRASNAY, G-chain 13.10.4 FRASNAY, group-compatibility theorem (recollement) 13.3.2 FRASNAY, indicative group theorem 13.7.2 13.9 FRASNAY, indicator 13.6 FRASNAY, monomorphy threshold 13.10.6 13.12.1 FRASNAY, reduction and compatibility thresholds 13.10 FRASNAY, reduction theorem 13.9.2 FREDRICKSON, Ramsey numbers 3.1.6 FREDRICKSON, Schur numbers 3.8.3 Free amalgam, freely amalgamable set A.2.2 Free interpretability 9.2 Free interpretability, free operator 9.3 Free subset (in a poset) = antichain 2.2.6 Function= mapping 1.1.2 Fundamental rank 1.4.2 G-compatible chains 13.3 G.chain, (G, A).chain 13.10.3 GALVIN, initial interval theorem 3.2 3.7 GARDINER, homogeneous graphs A.1.7 Generalized cartesian product 1.1.9 Generalized Continuum Hypothesis 1.5.4 1.9.3 Generated by chains (group) 13.5 Generating an ultrafilter (set) 2.3.4 GIRAUD, Ramsey numbers 3.1.4 GLEASON, Cantor theorem for posets 5.2.3 GLEASON, Ramsey numbers 3.1.4 3.1.5 GOEDEL, axiom of choice 1.2.4 GOEDEL, axiom of constructibility 2.1.5 GOEDEL, definition by recursiion 1.2.10 GOLOMB, Schur numbers 3.8.3 Good barrier sequence 7.2.1 Good coloration 3.8.1 Good sequence 4.2.1 GRAHAM, Ramsey numbers 3.1.6 Graph A.1.4 Graph, graph with two types of edges A.2.6 Graph, Rado graph A.1.5 GRAVER, Ramsey numbers 3.1.5 GREENWOOD, Ramsey numbers 3.1.4 3.1.5 GRINSTEAD, Ramsey numbers 3.1.5 Group, closed under adherence 12.3.4 Group, contracted 13.5 Group, dilated 13.4 Group, generated by chains 13.5 Group, indicative 13.6 Group, n-transitive 12.3.3 Group-compatibility theorem = recollement (Frasnay) 13.3.2 HAGENDORF, condition of indecomposability 5.6.1 5.12.1 HAGENDORF, decreasing sequence 5.5.2 HAGENDORF, faithful extension 8.1 8.2 HAGENDORF, immediate extension of a chain 5.6.2 5.6.3 HAGENDORF, immediate extension of a relation 5.1.3 5.2 HAGENDORF, indivisible chain 6.8.2 HAGENDORF, right indecomposable chain 6.3.6 HAGENDORF, unique sum-decomposition 6.3.4 HAJNAL, edge-indivisible graph A.5.2 HALPERN, ultrafilter axiom 2.3.5 HANSON, Schur numbers 3.8.3 HARTOGS aleph 1.6.4 HATCHER, characterization of an ordinal 1.2.8 HAUSDORFF, decomposition 6.2.1 HAUSDORFF, Hausdorff generalized construction 9.9 HAUSDORFF, induction scheme 6.2.7 HAUSDORFF, maximal chain axiom 2.2.4 HAZIM SHARIF, inextensive posets or tableaux 8.5.2 Height 2.7.1 Height of a direct product of posets 4.8.3 HENSON, denumerable homogeneous relations 12.2.2 HENSON, set of finite tournaments A.2.6 Hereditarily finite set 1.4.1 Hereditarily indecomposable = h-indecomposable chain 7.4 Hereditarily transitive set = ordinal 1.2.8 HESSENBERG, Hessenberg based product and exponentiation 9.9.2 HESSENBERG, natural sum and product 4.8.2 HIGMAN, initial intervals of a well partial ordering 4.4.1 HIGMAN, words 4.5.2 7.5.4 7.6.5 HILL, Ramsey numbers 3.1.6 HIRAGUCHI, dimension of a poset 4.9.6 HIRSCHFELD, saturated relation 11.3.4 HOBBY, orbits 12.4.2 Hodges 1.1.8 HODGES, adjacent elements and reduction threshold 13.10.1 13.11 HODGES, age without any saturated representative 11.3.6 HODGES, characterization of constant relations 9.4.2 9.5.2 HODGES, domain strictly subpotent with the range 10.11.1 HODGES, extension of a 1-morphism 11.3.3 HODGES, minimal bad sequence 4.2.3 HODGES, separation theorem 3.2.4 Homogeneous representative A.2.6 Homogeneous, p-homogeneous system 12.3.1 Homogeneous, p-homogeneous, ( 12.1.1 Homomorphic image of a chain 2.6.2 Hypergraph A.1.4 Ideal in a poset 2.13 Ideal in a poset, mutually incomparable ideals 4.7.3 Identical on a set (filter) 10.1.5 Identity group 13.6.2 ILLE, elementary extensive interval-closure 11.7.4 ILLE, three propositions on interval-closure 11.9 Immediate extension, chains 5.6 Immediate extension, relations 5.1.3 Inaccessible cardinal 2.8.9 Incidence matrix 3.4.1 Inclusion 1.1 Incomparable elements a|b 1.6.1 Incomparable finite posets under embeddability 5.2 Incompatibility lemma for rel-ages 11.2.2 Increasing number of orbits 12.4 Increasing profile 3.6.1 Indecomposable chain 6.3 Indecomposable chain, right indecomposable initial interval 6.3.3 Indecomposable chain, right or left indecomposable chain 6.3.1 Indecomposable ordinal 1.3.6 Indecomposable ordinal sequence 7.6 Index (in a sequence) 1.2.2 Indicative group 13.6 Indicative group, indicator 13.6.2 Indicative group, Q-indicative group 13.7.1 Indivisibility theorem 6.8.2 11.6.4 Indivisible relation, indivisible chain 6.8 10.3.3 Induced (k,p)-equivalence class or isomorphism class 11.8.2 Induced rel-age 11.1.3 Induction = transfinite induction 1.2.10 Induction scheme for scattered chains 6.2.7 Inexhaustible relation 10.6 Inexhaustible relation, inexhaustible age 10.6.2 Inexhaustible relation, inexhaustible extension theorem 10.6.3 Inexhaustible relation, strongly inexhaustible relation or system A.3.5 Inextensive, poset of height two 8.5.1 Inextensive, tableau 8.4 Inextensivity theorem 8.5.6 Inf-restriction (barrier) 7.2.3 Infimum (inf) 2.1.2 Infinite set, Dedekind 1.1.4 Infinite set, Tarski 1.1.1 Infinity axiom 1.2.4 Initial interval 2.2.1 Initial interval generated by a sequence 4.1.2 Initial interval generated by a set 4.1.1 Initial interval of a sequence 4.1.4 Initial interval, set of initial intervals = 2.5.1 Initial intervals of a well partial ordering 4.4.1 Initial segment of a given length A.4.11 Initially maximal chain 2.11.5 Injectable ordinal 1.6.4 Injection = infective function 1.1.2 Injective filter 10.1.2 Injective operator 9.3.2 Inside a cut (element) 2.6.5 Integer = non-negative integer = natural number = finite ordinal 1.2.3 Integer = non-negative integer = natural number = finite ordinal, set of integers ( 1.2.4 Intermediacy = betweenness relation associated with a chain 9.2.1 interval 2.2.1 Interval of a relation 9.8 Interval, strong interval of a poset 9.8 Interval-closure, interval-filter 11.7 Interval-ordering (well-founded) 2.2.5 Inverse function 1.1.2 IRVING, Ramsey numbers 3.1.6 ISBELL, Ramsey numbers 3.1.4 Isolated element (topology) 6.6.5 Isolated rel-age, isolating pair 12.8.1 Isomorphic, isomorphism 1.6 1.7.6 Isomorphic, isomorphism type 1.7.7 Isomorphic, R-isomorphic h-tuples 9.8.3 JEAN, non trivial universal class 13.3.4 JEAN, tournament and monomorphy 9.7 Jech 1.1.8 JECH, dependent choice 1.8 JECH, ordering axiom 2.4.4 JECH, Suslin tree 5.8 JENSEN, Suslin chain 5.8 JOHNSBRATEN, Suslin chain 5.8 JONSSON, homogeneous relation 12.2.2 JORDAN, hypothesis on transitive finite groups 9.7.3 12.3.3 JULLIEN, faithful extension 8.2 JULLIEN, incomparable finite posets 5.2 JULLIEN, right and left indecomposable chain 6.3.4 6.3.6 JULLIEN, Szpilrajn chain 8.6.6 8.6.7 13.10.2 k-uniform hypergraph A.1.4 KALBFLEISCH, Ramsey numbers 3.1.5 3.1.6 KANTOR, incidence matrix and linear independence 3.4.2 KEISLER, 1-extension 10.1.6 Keith DEVLIN, Suslin chain and tree 5.8 Kernel of a finitist relation 10.8.1 Kernel of a solid morphism 11.6 Kernel of an almost chainable relation 10.9.3 KERY, Ramsey numbers 3.1.5 KLAUA, transfinite real 4.8.2 KNASTER, fixed-point lemma 1.1.3 KOENIG, lemma 4.6.1 5.2.2 KOENIG, theorem 1.1.9 KOMJATH, indivisible graph A.4.11 KONG, stratified poset 2.10.1 KRAUSS, (G, A)-chain 13.10.3 KRAUSS, universal class 5.10.3 KREHER, Ramsey numbers 3.1.6 KRUSKAL, ordering of finite trees 5.4 KUNEN, decreasing 5.2 5.11.2 KURATOWSKI, couple 1.1.2 KURATOWSKI, maximal chain axiom 2.2.4 KURATOWSKI, separation lemma 2.3.3 KUREPA, Aronszajn tree 5.9.1 KUREPA, maximal chain in a finite tree 2.11.2 l-covering (hypergraph) A.4.10 LACHLAN, adjacent elements and reduction threshold 13.10.1 13.11 LACHLAN, homogeneous graphs A.1.7 LACHLAN, indivisible homogeneous systems A.4.2 Large set A.5.4 LARSON, problem of Hagendorf 6.3.6 LAUCHLI, ordering axiom 2.4.4 LAVER, forerunner 7.3.1 LAVER, hereditarily indecomposable chain 7.4.2 7.4.3 LAVER, indivisible chain 6.8.2 LAVER, well quasi-ordering of scattered chains 7.5.4 Left bound of a cut 2.6.5 Left indecomposable chain 6.3.1 Length of a sequence 1.2.2 Less than relation 4.1.2 Levy 1.2.5 LEVY, ultrafilter axiom 2.3.5 Lexicographic partition of edges A.5.2 Lexicographically ordered set of a barrier 7.1.3 Lexicographically ordered set, lexicographic rank 3.2.1 LI WEI, Ramsey numbers 3.1.6 Limit aleph 1.6.5 Limit element of a convergent ordinal sequence 6.6.2 6.6.4 Limit ordinal 1.2.4 Linear (or totally ordered) augmentation 2.9.3 Linear independence lemma 3.4.2 LIVINGSTONE, increasing number of orbits 12.4 Local isomorphism 9.1.4 Local isomorphism, local automorphism 9.1.6 LOEWENHEIM 10.1.7 LOPEZ, another proof of Galvin 3.7 LOPEZ, automorphism lemma 9.1.2 LOPEZ, bivalent tableau 8.4 LOPEZ, counterexample 8.3.2 LYGEROS, computation of posets 2.14 MACPHERSON, countable representatives of an age 10.2.4 MACPHERSON, homogeneous structure A.2.8 MALITZ, counterexample 8.3.1 MALITZ, universal class 5.10.4 Mapping 1.1.2 Mapping, mapping extension property A.1 MATHIAS, augmentation and ordering axioms 2.9.3 Matrix (incidence) 3.4.1 Maximal antichain 2.2.6 Maximal augmented chain theorem (De Jongh, Parikh) 4.11.2 Maximal chain 2.2.3 Maximal chain of inclusion 2.5.3 Maximal chain, maximal chain axiom (Hausdorff — Zorn) 2.2.4 Maximal ideal axiom 2.13 Maximal rel-age 11.2 Maximal, minimal element (in a poset) 1.6.1 Maximalist extension theorem 11.2.5
Реклама
 |
|
О проекте
|
|
О проекте



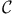 ) = set of
) = set of 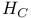
 )-homogeneous relation
)-homogeneous relation 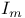
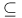 , strict inclusion
, strict inclusion 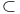

 )
) 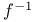 , inverse transformation
, inverse transformation 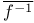
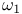 -sequence of denumerable posets
-sequence of denumerable posets