|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Veblen O., Young J.W. — Projective Geometry. Vol 1 |
|
|
 |
| Предметный указатель |
Polar forms 256
Polar forms, with respect to linear complex 324
Polar forms, with respect to regulus 302
Polar forms, with respect to set of n-points 256
Polar reciprocal figures 123
Polar, equation of 181 ex.
Polar, with respect to conic 120—125 284 285
Polar, with respect to n-line 84 exs.13 14
Polar, with respect to triangle 46
Polar, with respect to triangle, theorems on 54 ex.
Polar, with respect to two lines 52 exs.3 5
Polarity, in planar field 263 279 282 283
Polarity, in space 302
Polarity, null 324
Pole, with respect to canic 120
Pole, with respect to null system 324
Pole, with respect to regulus 302
Pole, with respect to triangle 46
Pole, with respect to two lines 52 ex.
Poncelest, J.V. 29 36 58 119 123
Problem, algebraic, transcendental 238
Problem, degree of 236 238
Problem, of projectivity 250 ex.
Problem, of second degree 245
Product, of points 145 231
Product, of two correspondences 65
Project, a figure from a point 36
Project, ABC can be projected into A'B'C 59
Project, an element into 58
Projection, of a figure from a point 34
Projective collineation 71
Projective conies 212 304
Projective correspondence or transformation 13 58
Projective correspondence or transformation, general group on line 68
Projective correspondence or transformation, in plane 268
Projective correspondence or transformation, of two- or three- dimensional forms 71 152
Projective geometry distinguished from metric 12
Projective pencils of points on skew lines are axially perspective 64
Projective projectivities 208
Projective space 97
Projectivities, commutative, example of 70
Projectivities, on sides of invariant triangle of collineation 274 276 ex.
Projectivity, ABC-A'B'C' 59
Projectivity, ABCD-ABDC implies H(AB, CD) 103
Projectivity, ABCD-BADC 60
Projectivity, analytic expression for, between pencils in plane 183
Projectivity, analytic expression for, between points of different lines 167
Projectivity, assumption of 95
Projectivity, axis (center) of, on conic 218
Projectivity, between two conies 212—216
Projectivity, definition and notation for 58
Projectivity, for space 97
Projectivity, fundamental theorem of, for line 95
Projectivity, fundamental theorem of, for linear net 94
Projectivity, fundamental theorem of, for plane 96
Projectivity, homogeneous analytic expression for 164
Projectivity, if H(12, 34), then 1234—1243 82
Projectivity, in one-dimensional forms is the result of two perspectivities 63
Projectivity, involution belonging to 226
Projectivity, necessary and sufficient condition for MMAB-MMA'B' is Q (MAB, MB'A') 101
Projectivity, necessary and sufficient condition for MNAB-MNA'B' is Q(MAB, NB'A') 100
Projectivity, nonhomogeneous analytic expression for 154—157 206
Projectivity, on conic 217—221
Projectivity, parabolic 101
Projectivity, principle of 97
Projectivity, problem of 250 ex.
Projector 35
Properly projective 97
Properly projective, spatial net is 97
Quadrangle, any complete, may be transformed into any other by projective collineation 74
Quadrangle, complete 44
Quadrangle, complete, and quadrilateral, theorem on 63 ex.
Quadrangle, conies through vertices of, meet line in pairs of an involution 127
Quadrangle, if two, have same diagonal triangle, their eight vertices are on conic 137 ex.
Quadrangle, inscribed in conic 137 ex.
Quadrangle, opposite sides of, meet line in pairs of an involution 103
Quadrangle, perspective, theorem on 63 ex.
Quadrangle, quadrangle-quadrilateral configuration 46
Quadrangle, simple, theorem on 52 ex.
Quadrangles, if two, correspond so that five pairs of homologous sides meet on a line I, the sixth pair meets on I 47
Quadrangular section by transversal of quadrangular set of lines is a quadrangular set of points 79
Quadrangular section, of elements projective with quadrangular set is a quadrangular set 80
Quadrangular section, Q( ) is necessary and sufficient for ) is necessary and sufficient for  142 142
Quadrangular section, Q( ) is necessary and sufficient for ) is necessary and sufficient for  145 145
Quadrangular section, Q(ABC, A'B'C) implies Q(A'B'C, ABC) 101
Quadrangular section, Q(ABC, A'B'C) is the condition that AA', BB', CC' are in involution 103
Quadrangular section, Q(MAB, MB'A') is the condition for MMAB-MMA'B' 101
Quadrangular section, Q(MAB, NB'A') is the condition for MNAB-MNA'B' 100
Quadrangular set 49 79
Quadrangular set at planes 79
Quadrangular set of lines 79
Quadrangularly related 86
Quadratic binary form 252
Quadratic binary form, invariant of 252
Quadratic correspondence 139 exs.22 24
Quadric spread in 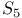 331 331
Quadric surface 301
Quadric surface, degenerate 308
Quadric surface, determined by nine points 311
Quadrilateral, complete 44
Quadrilateral, if two quadrilaterals correspond so that five of the lines joining pairs of homologous vertices pass through a point P, the line joining the sixth pair of vertices will also pass through P 49
Quantic 254
Quaternary forms 258
Quotient of points 149
Range, of conies 128—136
Range, of points 55
Ratio, of points 149
Rational operations 149
Rational space 98
Rationality, domain of 238
Rationality, net of, on line 84 85
Rationality, planar net of 86—88
Rationality, spatial net of 89—93
Rationally related 86 89
Reducible equation 239
Reflection, point-line, projective 223
Reflexive correspondence 66
Regulus, conjugate 299
Regulus, degenerate cases 311
Regulus, determined by three lines 298
Regulus, directrices of 299
Regulus, generated by projective conies 304 307
Regulus, generated by projective ranges or axial pencils 299
Regulus, generators or rulers of 299
Regulus, of a congruence 318
Regulus, picture of 300
Regulus, polar system of 300
Related figures 35
| Resultant, equal 65
Resultant, of two correspondences 65
Resultant, of two projectivities is a projectivity 68
Reye, T. 125 139
Rohn, K. 309
Salmon, G. 138
Sannia, A. 304
Scale, defined by three points 141 231
Scale, on a conic 231
Schroter, H. 138 281
Schur, F. 95
Science, abstract mathematical 2
Science, concrete application or representation of 2
Scott, C.A. 203
Section, conic section 109
Section, of figure by plane 34
Section, of plane figure by line 35
Segre, C. 230
Self-conjugate subgroup 211
Self-conjugate triangle with respect to conic 123
Self-polar triangle with respect to conic 123
Set, harmonic 80
Set, of elements projective with quadrangular set is quadrangular 80
Set, quadrangular 49 79
Set, synonymous with class 2
Set, theorems on harmonic sets 81
Seven-point, plane section of 53 ex.
Seydewitz, F. 281
Sheaf of planes 55
Side, false, of complete quadrangle 44
Side, of n-point 37
Similarly placed quadrangles 50
Simple element of space 39
Simple n-point, n-line, n-plane 37
Singly parabolic point 274
Singular point and line in nonhomogeneous coordinates 171
Six-point, in four-space section by three-space 54 ex.
Six-point, plane section of 54 ex.
Skew lines 24
Skew lines, four, are met by two lines 250 ex.
Skew lines, projective pencils on, are perspective 105 ex.
Space, analytic projective 11
Space, as equivalent of three-space 34
Space, assumption for, of n dimensions 33
Space, extended 242
Space, finite 201 202
Space, n- 30
Space, of three dimensions 20
Space, properly or improperly projective 97
Space, rational 98
Space, theorem of duality for, of three dimensions 28
Spatial net 89
Spatial net, is properly projective 97
Spatial net, theorems on 89—92
Steiner point and line 138 ex.
Steiner, J. 109 111 125 138 139 285 286
Steinitz, E. 261
Sturm, Ch. 129
Sturm, R. 231 250 287
subclass 2
Subgroup 68
Subtraction of points 148
Sum of two points 141 231
Surface, algebraic 259
Surface, quadric 301
Sylvester, J.J. 323
System affected by a correspondence 65
Tangent, to conic 112
Tangents to a point conic form a line conic 116
Tangents to a point conic form a line conic, analytic proof 187
Taylor's theorem 255
Ternary forms 258
Ternary forms, bilinear, represent correlation in a plane 267
Tetrahedra 326 ex.
Tetrahedra, configuration of perspective, as section of six-point in four-space 54 ex.
Tetrahedra, Mobius 105 ex.
Tetrahedra, perspective 43 44
tetrahedron 37
Tetrahedron, four planes joining line to vertices of, projective with four points of intersection of line with faces 71 ex.
Three-space 20
Three-space, determined uniquely by four points, by a plane and a point, by two nonintersecting lines 23
Three-space, theorem of duality for 28
Throw, algebra of 141 157
Throw, characteristic, of projectivity 205
Throw, definition of 60
Throws, two, sum and product of 158
Trace 35
Transform, of a group 209
Transform, of one projectivity by another 208
Transform, to 58
Transformation, of one-dimensional forms 58
Transformation, of two- and three-dimensional forms 71
Transformation, perspective 13
Transformation, projective 13
Transitive group 70 212 ex.
triangle 37
Triangle, diagonal, of quadrangle (quadrilateral) 44
Triangle, invariant, of collineation, relation between projectivities on sides of 274 276 ex.
Triangle, of reference of system of homogeneous coordinates in plane 174
Triangle, whose sides pass through three given collinear points and whose vertices are on three given lines 102 ex.
Triangles 105 ex. 116 247 138 ex.
Triangles, axes of perspectivity of three, in plane perspective from same point, are concurrent 42 ex.
Triangles, from four centers 105 ex.
Triangles, from six centers 246—248
Triangles, inscribed and circumscribed 250 ex.
Triangles, mutually inscribed and circumscribed 99
Triangles, perspective, from point are perspective from line 41
Triangles, perspective, from two centers 100 exs.1 2 3
Triangles, perspective, theorems on 53 exs.9 10 11
Triple system 3
Triple, point, of lines of a quadrangle 49
Triple, point, of points of a quadrangular set 49
Triple, triangle, of lines of a quadrangle 49
Triple, triangle, of points of a quadrangular set 49
Undefined elements in geometry 1
United position 15
Unproved propositions in geometry 1
Variable 58 150
Veblen, O. 202
Veronese, G. 52 53
Vertex, false, of complete quadrangle 44
Vertex, of cone 109
Vertex, of flat pencil 55
Vertex, of n-planes 37
Vertex, of n-points 36 37
von Staudt, K.G.C 14 95 125 141 151 158 160 286
Wiener, H. 65 95 230
Zeuthen, H.G. 95
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 ) is necessary and sufficient for
) is necessary and sufficient for 
 ) is necessary and sufficient for
) is necessary and sufficient for