|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Veblen O., Young J.W. — Projective Geometry. Vol 1 |
|
|
 |
| Предметный указатель |
Enriqnes, F. 56 286
Equation, of conic 185 245
Equation, of line (point) 174
Equation, of plane (point) 193 198
Equation, quadratic, has roots in extended space 242
Equation, reducible, irreducible 239
Equivalent number systems 150
Extended space 242 255
Extension, assumptions of 18 24
Face of n-point or n-plane 36 37
Fermat, P. 285
Field 149
Field, extended, in which any polynomial is reducible 260
Field, finite, modular 201
Field, pointy on a line form a 151
figure 34
Fine, H.B. 255 260 261 289
Finite spaces 201
Five-point, diagonal points, lines, and planes of, in space 204 exs.16 17 18
Five-point, in space may be transformed into any other by projective collineation 77
Five-point, plane section of, in space 39
Five-point, simple, in space determines linear congruence 319
Five-points, perspective, in four-space 54 ex.
Fixed element of correspondence 68
Flat pencil 55
Forms, linear binary 251
Forms, of nth degree 254
Forms, one-dimensional, of second degree 109
Forms, polar forms 256
Forms, primitive geometric, of one, two, and three dimensions 55
Forms, quadratic binary 252
Forms, ternary bilinear, represents correlation in plane 267
Four-space 25 ex.
Frame of reference 174
Fundamental elements 1
Fundamental points of a scale 141 231
Fundamental propositions 1
Fundamental theorem of projectivity 94—97 213 264
General point 129
Geometry, associated with a group 259
Geometry, distinction between projective and metric 12
Geometry, finite 201
Geometry, object of 1
Geometry, starting point of 1
Gergonne, J.D. 29 123
Grade, geometric forms of first, second, third 55
Group 66
Group, commutative 70
Group, examples of 69 70
Group, general projective, in plane 268
Group, general projective, on line 68 209
Group, of correspondences 67
Harmonic conjugate 80
Harmonic homology 223
Harmonic involutions 224
Harmonic set 80—82
Harmonic set, cross ratio of 159
Harmonic set, exercises on 83 84
Harmonic transformations 230
Harmonically related 84
Hesse 125
Hessenberg, G. 141
Hexagon, simple, inscribed in conic 110 111
Hexagon, simple, inscribed in three concurrent lines 250 ex.
Hexagon, simple, inscribed in two intersecting lines 99
Hexagram 304 ex.
Hexagram, of Pascal (hexagramma mysticum) 138 exs.19—21
Hilbert, D. 3 95 148
Holgate, T.F. 119 125 139
Homogeneous coordinates in plane 174
Homogeneous coordinates, geometrical significance of 165
Homogeneous coordinates, in space 11 194
Homogeneous coordinates, on line 163
Homogeneous forms 254
Homologous elements 35
Homology, axis and center of 104
Homology, canonical form of, in plane 274 275
Homology, harmonic 223 275
Homology, in plane 72
Homology, in space 75
Hyperosculate, applied to two conies 136
Ideal elements 7
Ideal points 8
Identical correspondence 65
Identical matrix 157 269
Identity (correspondence) 65
Identity (correspondence), element of group 67
Improper elements 239 241 242 255
Improper transformation 242
Improperly projective 97
Independence, necessary for distinction between assumption and theorem 7
Independence, of assumptions 6
Index, of group of collineations in general projective group in plane 271
Index, of subgroup 271
Induced correlation in planar field 262
Infinity, points, lines, and planes at 8
Inscribed and circumscribed triangles 98 250 ex.
Inscribed figure, in a conic 118
Invariant element 68
Invariant figure, of collineation is self-dual 272
Invariant figure, under a correspondence 67
Invariant subgroup 211
Invariant triangle of collineation, relation between projectivities on 274 276 ex.
Invariant, of binary form of nth degree 257
Invariant, of quadratic binary forms 252—254 ex.
Invariant, of two linear binary forms 252
Inverse operations (subtraction, division) 148 149
Inverse, of a correspondence 65
Inverse, of element in group 67
Inverse, of projectivity is a projectivity 68
Inverse, of projectivity, analytic expression for 157
Involution 102
Involution, analytic expression for 157 222 254 ex.
Involution, belonging to a projectivity 226
Involution, characteristic cross ratio of 206
Involution, complexes in 333
Involution, condition for 254 ex.
Involution, double points of, determined by covariant 258
Involution, double points of, in extended space 242
Involution, on conic 222—230
Involution, theorems on 102 103 124 127—131 133 134 136 206 209 221—229 242—243
Involutions, any projectivity is product of two 223
Involutions, harmonic 224
Involutions, pencil of 225
Involutions, two, have pair in common 243
Involutions, two, on distinct lines are perspective 243
Involutoric correspondence 66
Irreducible equation 239
Isomorphism 6
Isomorphism, between number systems 150
Isomorphism, simple 220
Jackson, D. 282
Join 16
Kantor, S. 250
Klein, F. 95 333 334
Ladd, C 138
Lage, Geometrie der 14
Lennes, N.J. 24
Lindemann, F. 289
Line conic 109
Line coordinates, in plane 171
Line coordinates, in space 327 333
Line, and conic, intersection of 240 246
Line, and plane on the same three-space intersect 22
Line, as undefined class of points 15
Line, at infinity 8
Line, equation of 174
Lineal element 107
Linear binary forms 251
Linear binary forms, invariant of 251
| Linear dependence, of lines 311
Linear dependence, of points 30
Linear fractional transformation 152
Linear net 84
Linear operations 236
Linear transformations, in plane 187
Linear transformations, in space 199
Lines, two, in same plane intersect 18
Luroth, J. 95
Maclaurln, C 119
MacNeish, H.F. 46
Mathematical science 2
Matrices, determinant of product of two 269
Matrices, product of 156 268
Matrix, as operator 270
Matrix, as symbol for configuration 38
Matrix, characteristic equation of 165 272
Matrix, conjugate, transposed, adjoint 269
Matrix, definition 156
Matrix, identical 157 269
Matrix, used to denote projectivity 156
Menachmus 126
Metric geometry 12
Midpoint of pair of points 230 ex.
Mobius tetrahedra 105 ex. 326 ex.
Multiplication of points 145 231
Multiplication of points, commutative law of, is equivalent to Assumption P 148
Multiplication of points, other definitions of 167 exs.3 4
Multiplication of points, theorems on 145—148
n-line, complete or simple 37 38
n-line, inscribed in conic 138 ex.
n-plane, complete in space 37
n-plane, on point 38
n-plane, simple in space 37
n-point 54 ex. 250 ex.
n-point, complete, in a plane 37
n-point, complete, in space 36
n-point, inscribed in conic 119 ex.
n-point, m-space section of, in (n + l)-space 54 ex.
n-point, plane section of, in space 53 exs.13 16
n-point, section by three-space of, in four-space 54 ex.
n-point, simple, in a plane 37
n-point, simple, in space 37
n-points, in different planes and perspective from a point 42 ex.
n-points, in same plane and perspective from a line 42 ex.
n-points, mutually inscribed and circumscribed 250 ex.
n-points, two complete, in a plane 53 ex.
n-points, two perspective, in (n—l)-space, theorem on 54 ex.
Net of rationality, coordinates in 162
Net of rationality, in plane 86
Net of rationality, in plane (space) left invariant by perspective collineation 93 exs.9 10
Net of rationality, in plane, theorems on 87 88 exs.92 93
Net of rationality, in space 89
Net of rationality, in space is properly projective 97
Net of rationality, in space, theorems on 89—92 exs.92 93
Net of rationality, on line (linear net) 84
Net of rationality, on line (linear net), theorems on 85
Newson, H.B. 274
Nonhomogeneous coordinates, in plane 169
Nonhomogeneous coordinates, in space 190
Nonhomogeneous coordinates, on a line 152
Null system 324
Number system 149
ON 7 8 15
Operation, geometric 236
Operation, linear 236
Operation, one-valued, commutative, associative 141
Operator, differential 256
Operator, polar 284
Operator, represented by matrix 270
Opposite sides of complete quadrangle 44
Opposite vertex and side of simple n-point 37
Opposite vertices, of complete quadrilateral 44
Opposite vertices, of simple n-point 37
Oppositely placed quadrangles 50
Order 60
Ordinate 170
Origin of coordinates 169
Osculate, applied to two conies 134
Padoa, A. 3
Papperitz, E. 309
Pappus, configuration of 98 99 100 126 148
Parabolic congruence 315
Parabolic point of collineation in plane 274
Parabolic projectivities, any two, are conjugate 209
Parabolic projectivity 101
Parabolic projectivity, analytic expression for 207
Parabolic projectivity, characteristic constants 207
Parabolic projectivity, characteristic cross ratio of 206
Parabolic projectivity, gives H(MA', AA") 207
Parametric representation, of conic 234
Parametric representation, of points (lines) of pencil 182
Parametric representation, of regulus, congruence, complex 330 331
Pascal, B. 36 99 111—116 123 126 127 138 139
Pencil, base points of 182
Pencil, of complexes 332
Pencil, of conies 129—136 287—293
Pencil, of involutions 226
Pencil, of points (lines), coordinates of 181
Pencil, of points, planes, lines 55
Pencil, parametric representation of 182
Period of correspondence 66
Perspective (n + l)-points in n-space 54 exs.20 26
Perspective collineation, in plane 71
Perspective collineation, in plane defined when center, axis, and one pair of homologous points are given 72
Perspective collineation, in space 75
Perspective collineation, leaving 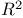 ( (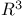 ) invariant 93 exs.9 10 ) invariant 93 exs.9 10
Perspective conic and pencil of lines (points) 215
Perspective correspondence 12 13
Perspective correspondence, between two planes 71 277 ex.
Perspective figures, from a line 36
Perspective figures, from a point or from a plane 35
Perspective figures, if A, B, C and A', B', C' on two coplanar lines are perspective, the points (AB', BA'), (AC', CA'), and (BC, CB') are collinear 52 ex.
Perspective geometric forms 56
Perspective n-lines, five-points in four-space 54 ex.
Perspective n-lines, theorems on 84 exs.13 14
Perspective tetrahedra 43
Perspective triangles 54 ex. 246 84 exs.7 10 11
Perspective triangles, sextuply 246
Perspective triangles, theorems on 41 53 exs.9 10 11
Perspectivity, between conic and pencil of lines (points) 215
Perspectivity, center of, plane of, axis of 36
Perspectivity, central and axial 57
Perspectivity, notation for 57
Pieri, M. 95
Planar field 55
Planar net 86
Plane figure 34
Plane section 384
Plane, and line on same three-space are on common point 22
Plane, at infinity 8
Plane, defined 17
Plane, determined uniquely by three noncollinear points, or a point and line, or two intersecting lines 20
Plane, equation of 193 198
Plane, of lines 65
Plane, of perspectivity 36 75
Plane, of points 55
Planes, three, on a three-space and not on a common line are on a common point 23
Planes, two, on same three-space are on a common line, and conversely 22
Planes, two, on two points A, B are on all points of line AB 20
Plucker's line coordinates 327
Point conic 109
Point figure 34
Point, and line determine plane 17 20
Point, as undefined element 15
Point, at infinity 8
Point, equation of 174 193 198
Point, of contact of a line with a conic 112
Points, three, determine plane 17 20
polar 84 exs.7 9 10 11
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



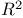 (
(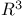 ) invariant
) invariant