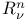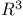|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| O'Neill B. — Semi-Riemannian Geometry: With Applications to Relativity |
|
|
 |
| Предметный указатель |
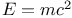 177 177
 -neighborhood 134 -neighborhood 134
 -related vector fields 14 -related vector fields 14
Acausal set 415
Acceleration 66 159
Achronal set 413
Action of group 254
Action of group, transitive 255
Ad(H)-invariance 301
Age of universe 352—353 362
Angular momentum, Newtonian 453
Angular momentum, Schwarzschild 373—374 380
Anti-isometry 92
Arc length 131
Arc length, first variation of 263 264
Arc length, local maximum and minimum of 272—276
Arc length, second variation of 266
Associated Newtonian particle 168
At rest in Newtonian space 161
At rest in Schwarzschild exterior 372
Atlas 2
Automorphism of Lie algebra 302
Automorphism of Lie group 300
Backwards Schwarz inequality 144
Backwards triangle inequality 144
Basis Theorem 8
Beem and Buseman’s example 209
Bending of light 381
Bi-invariant metric 304—306 330
Bianchi identity, first 75
Bianchi identity, second 76
big bang 348
Big crunch 348
Bilinear form, symmetric 46 53
Black hole 367 392—394
Black hole, formation of 385
Black hole, no escape from 392
Bochner’s theorem 259
Boost 236
Bracket operation in Lie algebra 447
Bracket operation on vector fields 13 31
Bump function 6
Canonical isomorphisms 26
Cartan, E. 224
Cauchy development 419—423
Cauchy horizon 428—431
Cauchy hypersurface 415—417 431
Cauchy hypersurface, future 438
Causal (nonspacelike) curve 146
Causal character of curve 69
Causal character of submanifold 142
Causal character of vector 56
Causal character of vector subspace 141
Causal cone 146 155
Causal future [past], 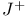 ![$[J^{-}]$](/math_tex/f3931fcef5a4e28d0293e520d234acab82.gif) 402 402
Causality conditions 407
Causality in Lorentz manifolds 293—298 401—437
Causality in Special Relativity 165—166
Causality relations 402
Chain rule 10
Christoffel symbols 62
Chronological future [past], 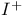 ![$[I^{-}]$](/math_tex/1feaec45bd1e00c80edbf4c9259cf46e82.gif) 402 402
Chronology condition 407
Clifton — Pohl torus 193 260
Closed geodesic 192
Closed subgroup 447
Codazzi equation 115
Codimension 20 98
Collision 179—181
Complete atlas 2 33
Complete semi-Riemannian manifold see “Geodesic completeness”
Complete vector field 29
Complete, metrically 138
Complex Grassmann manifold 326 327
Complex hyperbolic space 327
Complex projective space 327—329
Complex structure J on a vector space 324
Component, connected 21
Components of tensor 39 52
Conformal mapping 92
Congruence 102 120
Conjugate point 270—273
Conjugate point on cospacelike geodesics 274—277 299
Conjugate point on null geodesics see “Focal points”
Connectedness 21 72
Connectedness, geodesic 138
Connection 59
Connection, Levi-Civita 61
Connection, natural, on 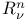 59 62 59 62
Connection, normal 118
Conservation lemma 252
Conservation of energy-momentum 179—181
Conservation of energy-momentum, infinitesimal 335
Conservation of Newtonian energy and momentum 453—454
Constant curvature 79—80
Constant curvature, manifolds of 113 223 227—231
Contraction of tensor, metric 83
Contraction of tensor, natural 40—42
Contravariant tensor 37
Convergence k 287—288 292 431—435
Convex open covering 131
Convex open set 129
Coordinate expression 4 5
Coordinate function 2
Coordinate neighborhood 3
Coordinate system 1—3
Coordinates, adapted to subset 16
Coordinates, associated Lorentz 167
Coordinates, cylindrical, on 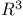 63 63
Coordinates, Euclidean 159
Coordinates, Kruskal-spherical 390
Coordinates, Lorentz (or inertial) 164
Coordinates, natural, on  1 1
Coordinates, normal 72—73
Coordinates, null 153 156
Coordinates, Schwarzschild 152
Coordinates, Schwarzschild-spherical 370
Coordinates, spherical, on 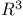 94—95 94—95
Coset manifold 306—309
Cosmological model 341
Cospacelike geodesic 273
Cotangent space 14
Covariant derivative 59 64
Covariant derivative of vector field on curve 65
Covariant derivative, normal 114 119
Covariant differential 64
Covariant tensor 37
Covering by subsets 21
Covering by subsets, open 21
Covering, manifold 444
Covering, map 443
Covering, semi-Riemannian 191 201—202
Critical point 33
Critical point of E 290
Critical point of length function 268
Cross section (or section) xiii
Cross section (or section), local 32
Curl 95
Curvature and gravity 334
Curvature operator 74
Curvature tensor, Riemannian (or Riemann — Christoffel) 74 96
Curvature tensor, Riemannian (or Riemann — Christoffel), components of 76 83
Curvature tensor, Riemannian (or Riemann — Christoffel), normal 125
Curvature tensor, Riemannian (or Riemann — Christoffel), sign of 89
Curvature tensor, Riemannian (or Riemann — Christoffel), symmetries of 75
Curvature, Gauss — Kronecker 197
Curvature, Gaussian 81
Curvature, holomorphic 325
Curvature, mean see “Mean curvature”
Curvature, normal see “Normal curvature vector”
| Curvature, Ricci 87—89
Curvature, Riemannian see “Curvature tensor”
Curvature, scalar 88
Curvature, sectional 77—79
Curvaturelike function 79
Curve 10
Curve segment 11
Curve, causal (nonspacelike) 146
Curve, null 69
Curve, parameter 122
Curve, periodic 29
Curve, piecewise smooth 11
Curve, regular 11
Curve, spaceUke 69
Curve, timelike 69
Dajczer and Nomizu’s criteria 53
de Sitter spacetime 229
Deck transformation 185
Derivation 12
Diameter of Riemannian manifold 279
Diffeomorphism 55
Differential form 43
Differential map 9
Differential of function 15 33
Dimension of manifold 3
Direct product and direct sum 34
Displacement vector 131 165
Distance in Robertson — Walker cosmology 347
Distance in special relativity 166 171
Distance, Riemannian 134 136—138
Distant paralleUsm 67
Divergence 195 213
Dot product 1 47
Duality of symmetric spaces 321—323
Dust see “Friedmann cosmological models”
Edge of achronal set 413
Einstein addition law 172
Einstein equation 336
Einstein gravitational tensor 336
Einstein manifold 96
Einstein — de Sitter model 352 356 357
Einstein, A. 54 172 173 177 332 334 336
Endpoint of extendible curve 30
Energy, density of perfect fluid 339
Energy, Newtonian 159 177
Energy, relativistic 177—180 333
Energy, Schwarzschild 374
Energy-momentum as source of gravity 335
Energy-momentum of lightlike particle 178 333
Energy-momentum of material particle 176 333
Energy-momentum, conservation of 179—180
Euclidean space 1 3 55 228
Evelyn and Jean 183
Evenly covered 443
Event 160 163 333
Event horizon 438
Expansion of universe 347—348
Exponential map 70—71
Exponential map, examples of 73 104
Exponential map, Lie 449—450
Exponential map, normal 199
Extendible curve 30 438
Extendible geodesic 68 130
Extendible manifold 155 157
Extrinsic geometry 102
Fiber of vector bundle 197
Fiber of warped product 204 205
First variation of arc length 263—265
First variation of E 289
Fixed endpoint homotopy 441
Flat manifold 79
Flow 29
Focal point 283—284
Focal point on cospacelike geodesics 285—288
Focal point on null geodesics 290—293 296 298
force 159
Frame (orthonormal) 84
Frame field 84—85
Frame-homogeneous manifold 258—259 260
Free fall 164 334
Friedmann cosmological models 350—353 356—357 362
Fundamental group 442
future 163
Future Cauchy hypersurface 438
Future cone (causal, null, timelike) 163
Future-convergence 435 436
Future-pointing curve 163
Future-pointing vector 163
G-invariant metric 310
G-orientation 241
Galaxies 341
Galaxies, idealizations of 341—342
Gauss equation 100 101 107
Gauss lemma 126—127
Gauss map 196
Gauss, K.F. 54 74
Gaussian curvature 81 124
General (or full) linear group GL(n,R) 446
General (or full) linear group GL(n,R), complex 449
General relativity, foundations of 332—337
Geodesic 67
Geodesic completeness 68
Geodesic completeness from point 138
Geodesic completeness, null 154
Geodesic completeness, spacelike 154
Geodesic completeness, timelike 154
Geodesic symmetry 223
Geodesic, broken 72
Geodesic, causal character of 69
Geodesic, closed 192—193
Geodesic, inextendible (maximal) 68
Geodesic, minimizing (shortest), maximizing (longest) 136—138 156 409 411
Geodesic, minimizing (shortest), maximizing (longest), locally 272 276
Geodesics in cylinders 148
Geodesics in hyperquadrics 149—150
Geodesics in submanifolds 102—103
Geodesics in surfaces 150—153
Geodesics, local properties of 133—135 147—148
Geodesics, variational properties of 263—299
Geometric units 162
Geroch, R.P. 423
Geroch’s example 154
Global hyperbolicity 412
Global symmetry 224 231
Gradient 85
Grassmann manifold, complex 326 327
Grassmann manifold, real 308 310
Hadamard’s Theorem 278
Hawking, S.W. 401
Hawking’s singularity theorem 431—434
Hermitian scalar product 324
Hessian and index form 268—269 290
Hessian of function 33 86
Holomorphic curvature 325
Homogeneous space 257
Homogeneous space, naturally reductive 312
Homogeneous space, normal 330
Homogeneous space, reductive 310
Homomorphism of fundamental groups 443
Homomorphism of Lie algebras 448
Homomorphism of Lie groups 329
Homothety 92
Homotopy, fixed endpoint 441
Hopf — Rinow theorem 138
Hopf’s corollary 228
Horizontal, subspace 205—212
Horizontal, vector (field) 205 212
Hubble law 347
Hubble time 348
Hyperbolic angle 144 156
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



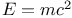
 -neighborhood
-neighborhood  -related vector fields
-related vector fields 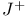
![$[J^{-}]$](/math_tex/f3931fcef5a4e28d0293e520d234acab82.gif)
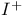
![$[I^{-}]$](/math_tex/1feaec45bd1e00c80edbf4c9259cf46e82.gif)