|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| O'Neill B. — Semi-Riemannian Geometry: With Applications to Relativity |
|
|
 |
| Предметный указатель |
Semiorthogonal group 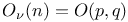 , fundamental group 310 , fundamental group 310
Semiorthogonal group 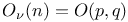 , Lie algebra 235 , Lie algebra 235
Semiorthogonal linear operator (matrix) 234—238 243 262
Separation 166
Shape operator 107 119
Shape tensor 100 118—121
Sign of curvature tensor 89
Sign of curve 263
Sign of hypersurface 106
Signature 50
Signature, matrix 234
Simple connectedness 442
Simply connected covering 444
Singularity theorem 401
Singularity theorem, Hawking’s 431—432
Singularity theorem, Penrose’s 436
Smooth Euclidean function 1
Smooth mapping of manifolds 4—5
Smooth overlap 2
Space form 227 243—248
Space form, classification of simply connected 227—228
Space form, positive and negative 244
Space-orientation (Space-orientability, Space-oriented) 237 240—242
Spacelike curve 69
Spacelike submanifold (or Riemannian submanifold) 57 142
Spacelike subspace 141
Spacelike vector 56
Spacetime 163 (see also “Individual spacetimes”)
Special orthogonal group  452 452
Special orthogonal group  , compactness and connectedness of 237 309—310 , compactness and connectedness of 237 309—310
Special orthogonal group  , fundamental group of 310 , fundamental group of 310
Special orthogonal group  , Lie algebra of 45 , Lie algebra of 45
Special relativity 158—184
Special relativity and general relativity 332—333
Special unitary group SU(n) 452
Special unitary group SU(n), Lie algebra of 452
Special unitary group SU(n), simple connectedness of 310
speed of light 161—162
Sphere as smooth manifold 3 20 307
Sphere, geometry of 57 94 101 103—104 105 113 137 228 271 318—319
Star 364 384—385
Static spacetime 360—361 363
Stress-energy tensor 335—337 340
Stress-energy tensor of perfect fluid 337—339
Strong energy condition 341
Submanifold, semi-Riemannian 57 97—125
Submanifold, semi-Riemannian, extremal 299
Submanifold, semi-Riemannian, totally geodesic 104—106 125
Submanifold, semi-Riemannian, totally umbilic 106 108
Submanifold, smooth 15—18
Submanifold, smooth, open 3—4
Submersion, semi-Riemannian 212—213
Submersion, smooth 20—21 32 33
Support 6
surface 3 (see also “Semi-Riemannian surface”)
Surface theory, classical 124
Surface theory, semiclassical 262
Symmetric space 224 231
Symmetric space, Lie construction of 315—317
Symmetric space, Riemannian 319—321
Symplectic group Sp(n) 451 452
Symplectic group Sp(n), topological properties of 309—310
Synchronizable observer field 359
Synge’s formula 265
tan (tangential projection) 98 205 344 369
Tangent bundle 26—27
Tangent space 7
Tangent vector 6—7
Tensor (field) 35
Tensor (field), at point 37
Tensor (field), components of 39
Tensor (field), contravariant 35 37
| Tensor (field), covariant 35 37 42—43
Tensor (field), derivation 43 52
Tensor (field), metric equivalence of 83
Tensor (field), multiplication 36
Tensor (field), type 35
Tensor (field), type-changing 81—84 (see also “Contraction”)
Test particle 337
Tidal force (Ricci operator) 216 219 278 299 335 362
Tidal force (Ricci operator), Schwarzschild 385—386 399
Time dilation 171
time function 359
Time, Newtonian 159—160
Time, proper 163
Time-orientation (Time-orientability, Time-oriented) 144—145 194 237 240—242
Time-separation 409—411
Timecone 143
Timelike convergence condition 340
Timelike curve 69
Timelike curve, piecewise smooth 146
Timelike submanifold 142
Timelike subspace 141
Timelike vector 56
Topological hypersurface 413
Topological manifold 413
Topological properties of manifolds 21—23
Torsion tensor 93
Totally geodesic submanifold 104 125
Totally umbilic submanifold 106 116—118
Trace form on matrix Lie algebra 303
Transferred vector field 14
Transvection 231
Trapped subset 435
Trapped surface 435
Twin paradox 173
Two-parameter map 122—123
Umbilic point 105
Unit speed curve 132
Unitary group U(n) 451
Unitary group U(n), compactness and connectedness of 309—310 329
Unitary group U(n), fundamental group of 310
Unitary group U(n), Lie algebra of 452
Units, geometric and conventional 162
VACUUM 337
Variation of arc length 263—288
Variation of curve 215
Variation of E 288—293
Variation, geodesic 216
Variation, vector field (infinitesimal variation) 216
Vector bundle 197
Vector field on curve 65
Vector field on curve, perpendicular 218
Vector field on curve, tangent 218
Vector field on manifold 12
Vector field on mapping 27
Vector field on submanifold 97
Vector field on submanifold, normal 98
Vector field on submanifold, tangent 98
Vector field,  -related 14 -related 14
Vector space as manifold 25—26
Velocity 10 171
Velocity, parameter 171
Vertical subspace 205 212
Vertical vector (field) 205 212
Volume element 195
Warped product 204
Warped product, causality in 417—418
Warped product, curvature of 210—211
Warped product, fibers 205
Warped product, geodesics in 207—209
Warped product, leaves 205
Warped product, warping function of 204
Worldline 160 163
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



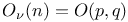 , fundamental group
, fundamental group 
 -related
-related