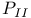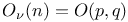|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| O'Neill B. — Semi-Riemannian Geometry: With Applications to Relativity |
|
|
 |
| Предметный указатель |
Hyperbolic space 111 113 156 228 278
Hyperbolic space, upper and lower imbeddings of 111
Hyperquadric 108—110
Hyperquadric, curvature of 113
Hyperquadric, frame-homogeneity of 113
Hyperquadric, geodesics in 112—113 149—150
Hyperquadric, isometrics of 113 239
Hyperquadric, product manifold structure of 110
Hyperquadric, sign of 108
Hypersurface 20 106—108 124
Hypersurface, totally umbilic 116—118
Identity component 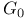 447 447
Imbedding, isometric 122
Imbedding, smooth 19
Immersed submanifold 19
Immersion, isometric 121—122
Immersion, smooth 19
Impact parameter 381
incomplete see “Complete entries”
Indefinite (or semi-) unitary group U(p,q) 324
Indefinite (or semi-) unitary group U(p,q), fundamental group 329
Indefinite (or semi-) unitary group U(p,q), Lie algebra 324
Index of scalar product 47
Index of scalar product space 51
Index of semi-Riemannian manifold 55
Index, form 269
Induced connection on submanifold 98—99
Induced topology 15—16
Inextendible see “Extendible entries”
Inner product 47
Instantaneous observer 180 333
Integral curve 27
Integral curve, maximal 28
Interpretations of tensors 36
Inverse function theorem 10
Involutive map 231
Isometric invariant 58
Isometry 58
Isometry group 233
Isometry group as Lie group 255
Isometry, local 90—91
Isotropy subgroup 255
Isotropy, local spatial 342
Isotropy, observed 341
Jacobi equation 216
Jacobi field 216 232
Jacobi identity 13 447
Jacobian function 196
Jacobian matrix 10
Kaehler manifold 325
Kepler’s laws 453—455
Killing form 302
Killing vector field 250—256
kinetic energy 159
Kobayashi’s proposition 321
Koszul formula 61
Kruskal plane 386—388 399 400
Kruskal spacetime 389—391
Kruskal spacetime, geodesics in 395—398
Kruskal spacetime, isometries of 399
Kruskal spacetime, truncated 392
Kulkarni’s theorem 229
Laplacian 86 213
Leaf of warped product 205
Left- and right-multiplication 447—448
Left-invariant vector field 448
Levi-Civita connection 61
Lie algebra 447
Lie algebra of Lie group 448
Lie algebra, abelian 301
Lie algebra, semisimple 306
Lie bracket see “Bracket operation”
Lie derivative 46 53 195 250
Lie exponential map 449 450
Lie groups, basic theory and examples 446—452
Lie groups, further properties 300—304 (see also individual Lie groups e.g. “Orthogonal
Lie subspace 310
Lift of functions, vectors, and vector fields 25 205
Lift of mapping 443
Lift of tensors 210
Light-like particle 163 380—384 392—393
Lightcone see “Nullcone”
Lightlike see “Null entries”
Lightlike submanifold 142
Lightlike subspace 141
Limit sequence 405
Line element 56
Linear isometry 51
Linear isomorphism xiii
Linear isotropy group 311
Linear operator 242—243
Local diffeomorphism 10
Local isometry 90 91
Local section 32
Locally symmetric semi-Riemannian manifold 215 219—224
Loop (or closed curve) 186
Lorentz coordinate system 164 167
Lorentz group 235 240
Lorentz manifold 55 126 143—149
Lorentz surface 150—153
Lorentz vector space 140
Lorentz — FitzGerald contraction 175
Lorentz, H.A. 158
Manifold, Lorentz 55
Manifold, Riemannian 55
Manifold, semi-Riemannian 54
Manifold, smooth 3
Manifold, smooth, construction of 23
Manifold, topological 413
Map (mapping), smooth 5
Marsden’s proposition 258
Mass of particle 159 163 177
Mass of Schwarzschild and Kruskal spacetimes 367 389
Matched covering 203
Material particle 163
Matter 335
Maximal geodesic 68
Maximal integral curve 30
Mean curvature 101 123 124
Metric equivalence 60
Metric tensor 54
Microwave background radiation 357
Minimizing geodesic 136
Minkowski space(time) 55 163
Minkowski, H. 158
Misner-completeness 156
Momentum, Newtonian 159
Momentum, relativistic 177—178 180
Myers’ theorem 279
Natural coordinate functions on  1 1
Newtonian gravitation 453—455
Newtonian motion 159—161
Newtonian space 159
Newtonian time 159
Nondegenerate bilinear form 46
Nondegenerate subspace 49
nor (normal projection) 98 205 344 369
Normal bundle 198
Normal bundle, exponential map of 199
Normal connection 114 118
Normal connection, covariant derivative 114 119
Normal connection, curvature tensor 125
Normal connection, parallel translation 119
Normal coordinates 72—73
Normal curvature vector 105 106 108
Normal neighborhood of point 71
Normal neighborhood of submanifold 199
Null geodesic and causality 404 430—431 435—437
Null geodesic in hyperquadrics 149—150
Null geodesic in surfaces 152 153
| Null geodesic, closed nonperiodic 193
Null geodesic, focal points on 290—298
Null geodesic, Kruskal 400
Null geodesic, Robertson — Walker 353—357
Null vector 48 56
Nullcone 53 56 109 128
NullSpace 53
Nullspace of index form 272 285
Observer 167
Observer field 358
Observer field, geodesic 358
Observer field, irrotational 358
Observer field, proper time synchronizable 359
Observer field, synchronizable 359
Observer, instantaneous 180 333
Observer, Schwarzschild 371
One-form 15
One-parameter subgroup 449
Open submanifold 3—4
Orbit of point 187
Orbit, free fall, in Schwarzschild spacetime 374—384
Orbit, manifold 187 188 191
Order of conjugate point 271
Order of focal point 283 291
Orientation (orientability, oriented) of hypersurface 189 197
Orientation (orientability, oriented) of manifold 23 189 195
Orientation (orientability, oriented) of vector bundle 198
Orientation (orientability, oriented) of vector space 189
Orientation (orientability, oriented), covering manifold 190
Orientation (orientability, oriented), natural, of  189 189
Orientation (orientability, oriented), space-orientation 237 240—242
Orientation (orientability, oriented), time-orientation see “Time-orientation”
Orientation-preserving map 190
Orientation-reversing map 190
Orthogonal coordinate system 64
Orthogonal group O(n) 451
Orthogonal group O(n), components of 238
Orthogonal group O(n), Lie algebra of 451
Orthogonal projection 50
Orthogonal vectors 48
Orthonormal basis 50
Orthonormal expansion 50
Pair isometry 102
Paracompactness 22
Parallel tensor field 65
Parallel translation 66
Parallel vector field on curve 66
Parameter curve 122
Partial derivative on manifold 7
Particle, Newtonian 159
Particle, relativistic (material and lightlike) 163
Partition of unity 22
Past (dual of future) 163 402
Past (dual of future) for Past entries see “Future entries”
Penrose, R. 401
Penrose’s singularity theorem 434—437
Perfect fluid 337—339 361 362
Perfect fluid, energy density of 339
Perfect fluid, pressure of 339
Perfect fluid, Robertson — Walker model of 345—347 362
Perihelion advance 378—380
Perp operation 49
Photon 163
Photon, frequency and wavelength of 179
Physical equivalence 336
Physical singularity 348
Piecewise smooth curve 11
Piecewise smooth curve segment 11
Piecewise smooth variation 264
Poincare half-plane 94 151 260
Poincare, H. 158 442
Polar map 221
Position vector field 26 128
Pregeodesic 69
Product manifold, semi-Riemannian 57 89
Product manifold, smooth 4 24
Product rule 44
Projective space, complex 327
Projective space, real 188 192 247 259
Proper time 163
Properly discontinuous group 188
Pseudohyperbolic space 110 (see also “Hyperquadric”)
Pseudosphere 110 (see also “Hyperquadric”)
Pullback 42
Q(v,w) 77
Quadratic form 47
Quasi-limit 404
Radiation cosmological model 353 362—363
Redshift, cosmological 354
Reductive homogeneous space 310
Reductive homogeneous space, naturally 312
Relative speed 172
Reparametrization of a curve 11 132
Rest photon in Kruskal spacetime 393 395
Restspace in general relativity 358
Restspace in special relativity 171
Ricci curvature 87
Ricci equation 125
Ricci flat 87
Riemann, G.F.B. 54
Riemannian manifold (metric) 55
Riemannian manifold (metric), completeness of 138
Riemannian manifold (metric), existence of 140
Riemannian symmetric space 319—321
Riemannian symmetric space of compact type 319
Riemannian symmetric space of noncompact type 319
Robertson — Walker spacetime, construction of 341—343
Robertson — Walker spacetime, cosmology of 347—350
Robertson — Walker spacetime, geodesics in 353
Robertson — Walker spacetime, perfect fluid in 345—346
Robertson — Walker spacetime, space of 343
Scalar curvature 88
Scalar product 47
Scalar product space 48—53
Scalar product space as semi-Riemannian manifold 58—59
Scalar product, Hermitian 324
Scalar product, natural Hermitian 324
Schwarz inequality 141
Schwarzschild black hole 367
Schwarzschild exterior 367
Schwarzschild free fall orbits 374—384
Schwarzschild half-plane  251 251
Schwarzschild observers 371
Schwarzschild radius function 365
Schwarzschild spacetime 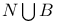 , construction of 364—367 , construction of 364—367
Schwarzschild spacetime 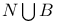 , curvature of 369 , curvature of 369
Schwarzschild spacetime 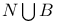 , extension of 386—390 , extension of 386—390
Schwarzschild spacetime 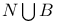 , geodesics in 372—384 , geodesics in 372—384
Schwarzschild strip 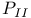 367 367
Schwarzschild time function 364
Second countability 21
Second fundamental form 100 107
Sectional curvature 77 124
Self-adjoint linear operator (matrix) 243 260—262
Semi-Euclidean space 55
Semi-Euclidean space, geodesics in 69
Semi-Euclidean space, isometries of 239—240
Semi-Riemannian covering 191 201
Semi-Riemannian hypersurface see “Hypersurface”
Semi-Riemannian manifold 54
Semi-Riemannian manifold, homogeneous see “Homogeneous space”
Semi-Riemannian manifold, isotropic 260
Semi-Riemannian manifold, locally symmetric 215 219—224
Semi-Riemannian manifold, symmetric see “Symmetric space”
Semi-Riemannian submanifold 57 97—125
Semi-Riemannian submersion 212—213
Semi-Riemannian surface 80—81 94 124 150—153 156 262
Semi-Riemannian warped product see “Warped product”
Semiorthogonal group 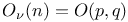 234 234
Semiorthogonal group 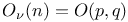 , components 236—238 , components 236—238
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте





 , construction of
, construction of