|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Graham C.C., McGehee O.C. Ч Essays in Commutative Harmonic Analysis |
|
|
 |
| ѕредметный указатель |
Saeki, S. (viii) 144 159 168 202 209 215 222 249 255 УL.
Saeki, S., and Sato, E., [1] 133 167 168 244 246
Saeki, S., [10] 6 73 90
Saeki, S., [11] 361
Saeki, S., [13] 118
Saeki, S., [14] 334
Saeki, S., [15] 90 412
Saeki, S., [16] 90 159 330 403
Saeki, S., [17] 85 410
Saeki, S., [18] 167 168 241
Saeki, S., [19] 168
Saeki, S., [1] 6
Saeki, S., [20] 189
Saeki, S., [21] 226
Saeki, S., [22] 168
Saeki, S., [2] 6
Saeki, S., [3] 268
Saeki, S., [4] 114
Saeki, S., [5] 294
Saeki, S., [6] 312
Saeki, S., [7] 65
Saeki, S., [8] 312 353
Saeki, S., [9] 90 334
Sagher, Y. listed with УRiviere N.M.Ф
Saka, K., [1] 133 137 238
Salem, R. 121 179 J.-P.Ф
Salem, R., [1] 93 100 179
Salem, R., [2] 18
Salinger, D.L., and Varopoulos, N.Th., [1] 159 330 403
Salinger, D.L., [1] 331 405
Sarason, D., [1] 103
Sarason, D., [2] 103
Sato, E. listed with УSaeki S.Ф
Sato, E., [1] 222
Saucer principle 331
Schneider, R., [1] 333 407
Schneider, R., [2] 333 407
Schoenberg, I.J., [1] 47
Schoenberg, I.J., [2] 324
Schreiber, B.M. listed with УIto T.Ф
Schreiber, B.M., [1] 73
Schwartz, J., [1] 297
Schwartz, J.T. listed with УDunford N.Ф
Schwartz, L. 71
Schwartz, L., [1] 70 72 313
Schwarz inequality see УInequality Cauchy
Section 354
Self, W.M., [1] 407
Semicharacter 122 126
Semigroup, semitopological 122
Semigroup, structure 126 134 143 246
Semigroup, topological 122 125 134
Separation property 355 356
Series, Taylor 127
Series, trigonometric 91
Set of analyticity 324ff.
Set of majorization 403
Set of synthesis 113 324 334 409 410
Set of uniqueness 91ff.
Set, 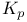 - 159 269 277 309 328 330 355 - 159 269 277 309 328 330 355
Set, 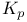 -, (definition) 269 -, (definition) 269
Set, 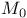 - 91ff. - 91ff.
Set, 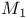 - 91ff. - 91ff.
Set, 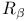 - 354 356 - 354 356
Set,  - 92ff. - 92ff.
Set,  - 91ff. 406 - 91ff. 406
Set,  - 91ff. - 91ff.
Set,  -Kronecker 355 -Kronecker 355
Set, 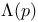 - 410 - 410
Set, algebraically independent 159
Set, algebraically scattered 145ff. 160 411
Set, appropriate 66
Set, Calderon 71
Set, Cantor 92 109 167 179
Set, cycle-free 354 412
Set, dense in bZ 222ff.
Set, diagonal 348
Set, Dirichlet 334
Set, dissociate 159ff. 197 199 210 220 325 411
Set, dissociate mod H 159ff.
Set, Ditkin 71 324
Set, ergodic 394 410
Set, H- 100
Set, Helson or non-Helson (vii) 48ff. 92 110 111 340 394 402ff. 407 409 410 412 HelsonФ)
Set, I- 409
Set, independent 34 64 65 78ff. 145ff. 159 160 225 269
Set, independent 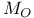 - 71 ff. 92 118ff. 167 239 257 - 71 ff. 92 118ff. 167 239 257
Set, independent mod H 159
Set, interpolation 157 158
Set, Kronecker or K- 65 85 110 113 114 159 222 225 269 277 309 328 330
Set, Kronecker or K-, (definition) 269
Set, M- 86 91ff.
Set, non-measurable 147 159
Set, non-triangular 324
Set, p-Helson 408
Set, peak 66
Set, perfect 70
Set, Riesz 409
Set, Sidon or non-Sidon 64 66 202 222 348 363 369 372 373 380 404 405 409 410 413 414 SidonФ)
Set, Sigtuna 363 391ff.
Set, strong Ditkin 6 70 71 73 324
Set, symmetric 88
Set, tail-dissociate 199 202
Set, totally disconnected 54
Set, U- 91ff.
Set, ultrathin 88 333
Set, V-Helson 353 412 V-HelsonФ)
Set, V-interpolation 353ff. 356
Set, V-Sidon 353ff. (see also УConstant V-SidonФ)
Set, Wiener-Ditkin 71
Shapiro, G.S. (viii) 168
Shapiro, G.S., [1] 67
Shapiro, H.S. listed with УFefferman C.Ф
Shapiro, H.S., [1] 33
Shapiro, H.S., [2] 293
Shatten, R., [1] 312
Sidon, constant see УConstantФ
Sidon, set see УSetФ
Sigtuna, Sweden 394
Silov, G.E. listed with УGelТfand I.M. and D.A.Ф
Silov, G.E., boundary 126 127 134 137 150 165 228 228ff. 361 411 412
Silov, G.E., boundary (definition) 228
Silov, G.E., Idempotent Theorem see УTheoremФ
Simmons, S.M., [1] 238
Simon, A.B. listed with УGoldberg R.R.Ф
Simon, A.B., [1] 231
Simon, A.B., [2] 159
Simon, A.B., [3] 159
Singleton 310 416
Sjoelin, P. listed with УCarleson L.Ф
Sleijpen, G.L.G., [1] 137
Smith, B.P., [1] 65
Smoothness conditions 3 82 334
SO(N) 319
Soardi, P.M. listed with Уde Michele L.Ф
Spector, R., [1] 137
Spector, R., [2] 137
Spectrum of a measure see УMeasureФ
Spence, L.E. listed with УFriedberg S.H.Ф
Spherical harmonic 318
Spine (=  ) 136 137 ) 136 137
Sreider, Y.A., [1] 133 202 420
Sreider, Y.A., [2] 182
Stafney, J.D., [1] 293
Stegeman, J.D., [1] 348 357
Stegeman, J.D., [2] 66
Stegeman, J.D., [3] 65
Stegeman, J.D., [4] 66 312
Stegeman, J.D., [5] 357
Stein, E.M., and Weiss, G., [1] 282 294 302 318
| Stein, E.M., [1] 282 347 297
Stein, E.M., [2] 282
Steinhaus, H., [1] 232
Stewart, J., [1] 47
Stone Ч Cech compactification see УCompactificationФ
Strichartz, R., [1] 407
Stromberg, K. listed with УHewitt E.Ф
Stromberg, K., [1] 238
Stromberg, K., [2] 209
Strong boundary point 132 229 239 242ff. 245
Strong boundary point, definition 228
Structure semigroup see УSemigroupФ
Sulley, L.J., [1] 133
Sup-norm algebra (= uniform algebra) 66 242
Support group of a measure 4 411
Support, theorem about 94
Symbolic (= functional) calculus see УFunctions that operateФ
Symmetric, maximal ideal see УIdealФ
Symmetric, Raikov system see УRaikov systemФ
Synthesis (= harmonic synthesis = spectral synthesis) 68ff. 92 101 103 308 313ff. 385ff. 409 416
Synthesis (= harmonic synthesis = spectral synthesis), algebra of 70
Synthesis (= harmonic synthesis = spectral synthesis), bounded 71 76ff. 84 85 410
Synthesis (= harmonic synthesis = spectral synthesis), curve that disobeys 410
Synthesis (= harmonic synthesis = spectral synthesis), fails for sphere 313
Synthesis (= harmonic synthesis = spectral synthesis), set of see УSetФ
Synthesis (= harmonic synthesis = spectral synthesis), singleton is of (for A(G)) 416ff.
Synthesis (= harmonic synthesis = spectral synthesis), singleton is of (for V) 310
System, Raikov see УRaikovФ
Tail-dissociate 199 202
Takeda, Z., [1] 47
Talagr, and, M., [1] 182
Talagr, and, M., [2] 222
Tam, K.W. 238
Tamarkin, J.D. listed with УHille E.Ф
Tame see УMeasureФ
Taylor Ч Johnson measure (= i.p. Hermitian probability measure) see УMeasureФ
Taylor, J.L. (vii) 412 R.G.Ф)
Taylor, J.L., [1] 125 128 133 134 136 137 144 230 246
Taylor, J.L., [2] 133 174 178 231
Taylor, J.L., [3] 125 128 133 246
Taylor, J.L., [4] 137 144
Taylor, J.L., [5] 136 137
Taylor, J.L., [6] 134 136 137
Tensor algebra 88 308ff. 412
Tensor algebra, automorphism 348ff.
Tensor algebra, endomorphism 353
Tensor algebra, tilde 335 357ff. 412
Tensor product 289 308ff.
Tensor product, complete 308
Tensor product, infinite 309 331
Tensor product, n-dimensional 336
Tensor product, of Banach spaces 308 312
Theorem for Fourier Ч Stieltjes transforms, extension 421
Theorem on 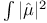 , N. WienerТs 19 225 236 415 , N. WienerТs 19 225 236 415
Theorem, about support 94
Theorem, BernsteinТs 280 293
Theorem, BochnerТs 41 268
Theorem, closed graph 280 387
Theorem, DruryТs 385
Theorem, EgorovТs 185
Theorem, F., and M.Riesz 28
Theorem, Generalized Purity 176 180 187 189
Theorem, Hausdorff Ч Young 285
Theorem, idempotent 2ff. 6 32 135 139
Theorem, Jessen Ч Wintner Purity 176
Theorem, Kns 331 340 347
Theorem, Kronecker 366 392
Theorem, Littlewood Ч Paley 297
Theorem, Local Peak Set see УTheorem RossiТs
Theorem, LusinТs 43 130
Theorem, MalliavinТs 90 313
Theorem, MarcinkiewiczТs 252 254
Theorem, MarcinkiewiczТs, converses to 261
Theorem, Markov Ч Kakutani fixed point 46
Theorem, Phragmen Ч Lindeloef 302
Theorem, Riesz representation 42 47 122 285
Theorem, Riesz Ч Thorin 285 287 289
Theorem, RossiТs Local Peak Set 239 241 246
Theorem, Silov Idempotent 358
Theorem, transfer 313
Theorem, VitaliТs 270 273
Theorem, VitaliТs (two-dimensional version) 271
Theorem, WendelТs 285
Theorem, Wiener Ч Levy 251 252
Theorem, Wiener Ч Levy (converses to) 255ff. 282
Theorem, ZafranТs 281ff. 294ff.
Topology, strong 126
Topology, strong, operator 126 291
Topology, weak 126
Topology, weak, operator 126 290 291
Transform, GelТfand 282 294
Transformation, measure preserving 18
Translation 231ff.
Translation, invariant subspace 68 72 408
trapezoid 418ff.
triangle 418ff.
U-set see УSetФ
Uniform algebra (= sup norm algebra) 66 242
Union question for Helson sets (vii) 48ff.
Union question for Kronecker sets 65
Union question for sets of bounded synthesis 84
Union question for sets of synthesis 409
Union question for Sidon sets 48ff. 414
Uniqueness see УSetФ
Uno, Y., [1] 293
Urbana (viii)
V(x,y) 308
V-Helson, constant see УConstantФ
V-Helson, set see УSetФ
V-interpolation set see УSetФ
V-Sidon, constant see УConstantФ
V-Sidon, set see УSetФ
Varopoulos, N.Th. (vii) 65 71 90 403 407 A.Ф УSalinger D.L.Ф)
Varopoulos, N.Th., [10] 324 335 348
Varopoulos, N.Th., [11] 312 361
Varopoulos, N.Th., [12] 354 355 356 357
Varopoulos, N.Th., [13] 65 222 401
Varopoulos, N.Th., [14] 65
Varopoulos, N.Th., [15] 66
Varopoulos, N.Th., [16] 65
Varopoulos, N.Th., [17] 66
Varopoulos, N.Th., [18] 353 412
Varopoulos, N.Th., [19] 66
Varopoulos, N.Th., [1] 174
Varopoulos, N.Th., [20] 66
Varopoulos, N.Th., [2] 215 268
Varopoulos, N.Th., [3] 209 215 265 268
Varopoulos, N.Th., [4] 114
Varopoulos, N.Th., [5] 312 324
Varopoulos, N.Th., [6] 312 324 330
Varopoulos, N.Th., [7] 312 324
Varopoulos, N.Th., [8] 72 324
Varopoulos, N.Th., [9] 121 231
Vermes, P. listed with УClume J.Ф
VitaliТs theorem see УTheoremФ
von Neumann, J., [1] 159
Waelbroeck, L., [1] 261
Weak 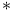 density number 98 density number 98
Weiss, G. listed with УCoifman R.R.Ф УKahane J.-P. and M.Ф УStein E.M.Ф
Weiss, M. listed with УKahane J.-P. and G.Ф
Weiss, M., [1] 202
Wells, B.B.Jr. listed with УRamsey L.T.Ф
Wells, B.B.Jr., [1] 408
Wendel, J.G., [1] 293
White, A.J. listed with УChow P.S.Ф УMcKilligan S.A.Ф
White, A.J., [1] 128
Wiener Ч Hopf operator 136
Wiener Ч Levy theorem see УTheoremФ
Wiener Ч Pitt phenomenon 168 202 230
Wiener, N. 19 255
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



 -
-  -
-  -
- 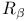 -
-  -
-  -
-  -
-  -Kronecker
-Kronecker 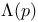 -
- 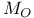 -
-  )
) 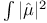 , N. WienerТs
, N. WienerТs  density number
density number