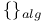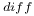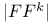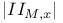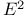Авторизация
Поиск по указателям
Ivey Th.A., Landsberg J.M. — Cartan for Beginners: Differential Geometry Via Moving Frames and Exterior Differential Systems
Обсудите книгу на научном форуме Нашли опечатку?
Название: Cartan for Beginners: Differential Geometry Via Moving Frames and Exterior Differential SystemsАвторы: Ivey Th.A., Landsberg J.M. Аннотация: This book is an introduction to Cartan's approach to differential geometry. Two central methods in Cartan's geometry are the theory of exterior, differential systems and the method of moving frames. The book presents thorough and modern treatments of both subjects, including their applications to classic and contemporary problems.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2003Количество страниц: 378Добавлена в каталог: 11.06.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
# 53 147 147 335 256 102 107 102 108 177 323 287 175 180 80 129 216 59 60 335 317 313 314 154 258 335 335 343 82 282 95 120 129 129 335 277 313 314 2 97 106 273 37 78 283 340 340 330 339 17 277 336 338 345 312 337 337 315 86 131 60 97 157 340 340 97 (I, J), linear Pfafflan system 164 (p, g)-forms 345 Abuse of notation 29 72 170 Adjoint representation 321 Affine connection 285 Affine tangent space 76 Algebraic variety 82 Algebraic variety, degree of 82 Algebraic variety, dimension of 82 Algebraic variety, general point of 83 Algebraic variety, ideal of 82 Almost complex manifold 274 282 344 Almost complex structure 344 Almost symplectic manifold 274 Ambrose — Singer Theorem 290 Ann(v) 129 Apparent torsion 165 Arclength parameter 14 ASO(2) 12 ASO(3) 23 ASO(3) as space of frames 24 Associated hypersurface 124 Associated varieties 123 Associative submanifolds 201 265 Associator 325 Asymptotic directions 80 Asymptotic line 60 226 238 Baecklund transformations 235—241 Baecklund's Theorem 237 Baseloc 80 Basic differential form 339 Bertini Theorem 112 Bertini Theorem, higher-order 112 Bertrand curve 26 Bezout's theorem 82 Bianchi identities 53—54 Bonnet surface 44 231 Burger's equation 208 232 Calibrated submanifold 198 Calibration 197 Calibration, associative 201 Calibration, Cayley form 202 Calibration, coassociative 201 Calibration, special Lagrangian 200 Canonical system on Grassmann bundle 177 Canonical system on space of jets 28 Cartan geometry 296 Cartan integer 156 179 Cartan lemma 314 Cartan system 209 Cartan — Dieudonne Theorem 331 Cartan — Janet theorem 192 Cartan — Kahler Theorem 254—256 Cartan — Kahler Theorem for linear Pfaffian systems 176 Cartan — Kahler Theorem for tableaux 156 Cartan — Kahler Theorem, Goldschmidt version 181 Cartan's algorithm for linear Pfaffian systems 178 Cartan's five variables paper 217 Cartan's test 256 Catenoid 43 Cauchy problem 349 Cauchy — Kowalevski form 350 Cauchy — Kowalevski Theorem 243 351 Cauchy — Riemann equations 347 Cauchy — Riemann equations, tableau 144 156 Cayley submanifold 202 Character of a tableau 156 Characteristic hyperplane 181 Characteristic systems (Monge) 213 Characteristic variety 157 Characteristic variety, dimension and degree of 159 Characteristics, Cauchy 205 259 Characteristics, Cauchy, quotient by 210 Characteristics, confounded 213 Characteristics, first-order 214 Characteristics, method of 207—208 Characteristics, Monge 213 Characters 258 Characters of linear Pfaffian system 179 Characters of tableau 154 Chebyshev net 227 Christoffel symbols 277 Cl(V,Q) 331 Clifford algebras 331 Clifford algebras, fundamental lemma of 332 Clifford torus 58 Co-roots 329 Coassociative submanifold 201 Codazzi equation for Darboux frames 43 Codazzi equation, matrix form 49 Codimension 245 Coisotropic hypersurface 124 Complete intersection 140 Complex characteristic variety 158 Complex contact structure 348 Complex manifold 343 344 Complex structure 318 344 Complexification of a real vector space 318 Cone 44 Cone over a variety 86 Cone, characterization of 125 Connection affine 285 Connection form 279 Connection on coframe bundle 278—283 Connection on induced vector bundles 284 Connection on vector bundle 277 Connection, symmetric 285 Conormal space, of submanifold in 77 Contact manifold 33 Contact system on space of jets 28 Contact, order of 83 Cotangent bundle 335 Cotangent space 335 Covariant differential operator 54 277 Cubic form 94 Curvature of curve in 14 Curvature of curve in 25 Curvature of G-structure 280 Curvature, Gauss 38 Curvature, Gauss, geometric interpretation of 47 Curvature, Gauss, in coordinates 4 Curvature, mean 38 Curvature, mean, geometric interpretation of 68 Curvature, mean, in coordinates 4 Curvature, Ricci 53 262 Curvature, scalar 53 262 266 330 Curvature, sectional 53 Curvature, traceless Ricci 330 Curvature, Weyl 330 Curvature-line coordinates 188 Curve in 14 Curve in 14 Curve in 25 Curve in 25—26 Curve in 25 Curve, arclength parameter 14 Curve, Bertrand 26 Curve, regular 13 Curve, speed of 14 Cylinder 44 d, exterior derivative 337 Darboux frame 42 Darboux's theorem 32 Darboux, integrable 218 239 Darboux, method of 217—222 Darboux, semi-integrable 222 de Rham Splitting Theorem 289 Decomposable tensor 312 Derived flag 216 Derived system 216 DET 102 315 Determinant of linear endomorphism 315 Developable surface 40 Differential form 336 Differential form, basic, semi-basic 339 Differential form, closed 338 Differential form, homogeneous 340 Differential form, left-invariant 17 Differential form, vector-valued 338 Differential ideal 340 Differential invariant, Euclidean 3 Dual basis 311 Dual variety 87 118 Dual variety, defect of 120 Dual variety, reflexivity 119 Dual vector space 311 Dupin, cyclides of 361 Dupin, theorem of 253 e-structure 304 Embedded tangent space 76 End(V) 312 Engel structure 217 Equivalent G-structures 275 Equivalent webs 268 Euclidean group 23 Euler characteristic 62 Exterior derivative 337—338 Exterior differential system 29 Exterior differential system with independence condition 27 Exterior differential system, hyperbolic 214—215 Exterior differential system, linear Pfaffian 164 Exterior differential system, Pfaffian 341 Exterior differential system, symmetries 204—205 F(M) 49 Face of calibration 199 First fundamental form (Riemannian) 46 First-order adapted frames (Euclidean) 45 Flag variety 85 316 Flag, A-generic 154 Flag, complete 85 Flag, derived 216 Flag, partial 85 Flat 3-web 268 Flat G-structure 275 Flat path geometry 296 Flat Riemannian manifold 52 Flat Riemannian manifold, isometric immersions of 194 Flat surface 41 Flow of a vector field 6 Flowbox coordinates 6 Flowchart for Cartan's algorithm 178 Focal hypersurface 89 Focal surface 237 266 Frame bundle, general 49 Frame bundle, orthonormal 50 Frame, Darboux 42 Frenet equations 25 Frobenius ideal 11 Frobenius structure 308 Frobenius system, tableau of 146 Frobenius theorem 10—12 30 Frobenius Theorem, proof 30 Fubini cubic form 94 Fubini forms 94 107 Fulton — Hansen theorem 130 Fundamental form via spectral sequences 98 Fundamental form, effective calculation of 97 Fundamental form, k-th 97 Fundamental form, prolongation property of 97 G(k, V), Grassmannian 72 G(n,m) 198 G-structure 267—275 G-structure, 1-flat 280 G-structure, 2-flat 281 G-structure, curvature 280 282 G-structure, definition 274 G-structure, flat 275 G-structure, prolongation 281 G/H-structure of order two 296 Gauss curvature in coordinates 4 Gauss curvature via frames 36—38 Gauss curvature, geometric interpretation of 47 Gauss equation 47 Gauss image 77
Реклама
 |
|
О проекте
|
|
О проекте



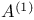
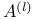
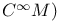
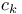 , codimension of polar space
, codimension of polar space 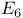 , exceptional Lie group
, exceptional Lie group 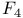 , differential invariant
, differential invariant 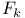
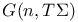
 , exceptional Lie group
, exceptional Lie group 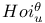
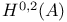
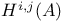
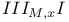
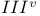
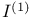 , derived system
, derived system 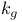
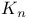
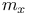 , functions vanishing at x
, functions vanishing at x 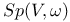 , symplectic group
, symplectic group 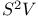
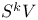
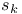 , characters of a tableau
, characters of a tableau 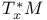 , cotangent space
, cotangent space 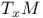 , tangent space
, tangent space 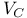 , complexification of V
, complexification of V 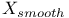
![$[R_{\theta}]$](/math_tex/89cb86e279b8f0fda7d4e8442deaa4f982.gif)
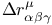
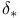 , dual defect
, dual defect 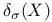 , secant defect
, secant defect 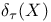 , tangential defect
, tangential defect 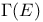 , smooth sections of E
, smooth sections of E 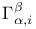
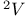
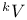
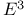 , Euclidean three-space
, Euclidean three-space 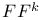
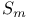 , spinor variety
, spinor variety 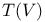
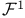 , Euclidean
, Euclidean 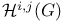
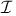 , differential ideal
, differential ideal 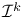 , k-th homogeneous component of
, k-th homogeneous component of 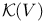
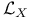 , Lie derivative
, Lie derivative 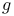 , Lie algebra of Lie group G
, Lie algebra of Lie group G 
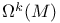 ,
, 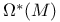
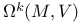
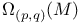
 , tensor product
, tensor product 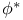 , pullback by
, pullback by 
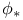 , pushforward by
, pushforward by 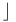 , interior product
, interior product 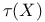 , tangential variety
, tangential variety 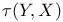
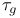
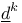
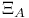 , characteristic variety of a tableau
, characteristic variety of a tableau