Авторизация
Поиск по указателям
Ivey Th.A., Landsberg J.M. — Cartan for Beginners: Differential Geometry Via Moving Frames and Exterior Differential Systems
Обсудите книгу на научном форуме Нашли опечатку?
Название: Cartan for Beginners: Differential Geometry Via Moving Frames and Exterior Differential SystemsАвторы: Ivey Th.A., Landsberg J.M. Аннотация: This book is an introduction to Cartan's approach to differential geometry. Two central methods in Cartan's geometry are the theory of exterior, differential systems and the method of moving frames. The book presents thorough and modern treatments of both subjects, including their applications to classic and contemporary problems.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2003Количество страниц: 378Добавлена в каталог: 11.06.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Gauss image, characterization of 93 Gauss map, algebraic 55 Gauss map, Euclidean 46 Gauss map, projective 77 Gauss map, varieties with degenerate 89 Gauss — Bonnet formula 64 Gauss — Bonnet theorem 62 Gauss — Bonnet theorem for compact hypersurfaces 64 Gauss — Bonnet theorem, local 60 Gauss — Bonnet — Chern theorem 65 Gauss' theorema egregium 48 General point 83 Generalized conformal structure 309 Generalized Monge system 139 Generic point 83 Geodesic 59 Geodesic curvature 59 Geodesic of affine connection 285 Geodesic torsion 60 GL(V) 316 Gr(k, V), orthogonal Grassmannian 75 Grassmann bundle 177 Grassmann bundle, canonical system on 177 Grassmannian 72 316 Grassmannian, isotropic 84 Grassmannian, tangent space of 73 Half-spin representation 107 Hartshorne's conjecture 140 Heat equation 350 Helicoid 39 Hermitian form 319 Hermitian inner product 319 Hexagonality 271 Higher associated hypersurface 124 Holomorphic map 345 Holonomy 286—295 Holonomy bundle 287 Holonomy group 287 Hom(V, W) 312 Homogeneous space 15 Hopf differential 230 Horizontal curve 287 Horizontal lift 287 Hyperbolic space 58 Hyperbolic space, isometric immersions of 197 Hyperplane section of a variety 88 Hypersurfaces in 55 Ideal, algebraic 340 Ideal, differential 340 Ideal, Frobenius 11 II, Euclidean second fundamental form 46 II, projective second fundamental form 77 III, projective third fundamental form 96 Incidence correspondence 88 Independence condition 27 Index of a vector field 61 Index of relative nullity 80 Induced vector bundle 283 Initial data 349 Initial value problem 349 Integrable extension 232 Integrable extension via conservation law 233 Integral curve 5 Integral element 27 Integral element, Kaehler-ordinary 245 Integral element, Kaehler-regular 249 Integral element, ordinary 256 Integral manifold 27 29 Integral, intermediate/general 219 Interior product 315 Involutive integral element 256 Involutive linear Pfaffian system 176 Involutive tableau 155 Isometric embedding 169—173 Isothermal coordinates 57 Isothermal coordinates, existence of 185 Isotropic Grassmannian 84 Isotropy representation 16 J(Y, Z), join of varieties 86 Jacobi identity 320 Jets 27 Join of varieties 86 Kaehler manifold 199 KdV equation 234 236 KdV equation, prolongation algebra 235 Killing form 323 Laplace system, tableau for 157 Laplace's equation 223 Laplacian 56 Left action 15 Left-invariant, differential form 17 Left-invariant, vector field 17 320 Level 155 Lie algebra 320 Lie algebra of a Lie group 17 Lie algebra, semi-simple 327 Lie algebra, simple 327 Lie bracket 336 Lie derivative 339 Lie group 316 Lie group, linear representation of 316 Lie group, matrix 16 316—318 Lie group, Maurer — Cartan form of 17 Lift 16 Lift, first-order adapted 37 Line congruence 237 Line of curvature 60 253 Line of curvature, isothermal coordinates along 188 Linear map 311 Linear map, transpose/adjoint of 312 Linear normality, Zak's theorem on 128 Linear Pfaffian systems 164 Linear Pfaffian systems, Cartan's algorithm for 178 Linear Pfaffian systems, involutivity 176 Linear projection of variety 88 Linear syzygy 111 Liouville's equation 218 237 Locally ruled variety 89 Locally symmetric 290 Majorants 150 Manifold, contact 33 Manifold, restraining 255 Manifold, symplectic 31 Matrix Lie groups 316—318 Maurer — Cartan equation 18 Maurer — Cartan form of a matrix Lie group 17 Maurer — Cartan form of an arbitrary Lie group 17 Maximal torus 327 Mean curvature in coordinates 4 Mean curvature vector 69 Mean curvature via frames 36—38 Mean curvature, geometric interpretation of 68 Minimal hypersurfaces 266 Minimal submanifold 197 Minimal surface 68 228—229 Minimal surface, Riemannian metric of 186 Minimizing submanifold 197 Minuscule variety 104 Modified KdV equation 234 Monge — Ampere equation 222 Monge — Ampere system 223 Monge's method 224 Moving frame 4 Moving frame, adapted 12 Multilinear 312 Multiplicity of intersection 83 Musical isomorphism 53 Newlander — Nirenberg theorem 345 Nijenhuis tensor 346 Non-characteristic initial data 157 Nondegenerate quadratic form 322 Normal bundle 46 66 Normal curvature 60 Normal space, of submanifold in 77 O(V, Q), orthogonal group 317 Octonions 324—326 Orthogonal Grassmannian 75 Orthogonal group 317 Orthogonal involutive Lie algebra 291 Osculating circle 14 Osculating hypersurface 109 111 Osculating quadric hypersurface 109 Parabolic subgroup 84 104 Parallel surfaces 225 Parallel transport 287 path geometry 295—308 Path geometry, definition of 295 298 Path geometry, dual 297 Path geometry, flat 296 Pfaff's Theorem 33 Pfaffian 322 Pfaffian system 341 Pfaffian system, linear 164 Picard's theorem 5 10 Poincare — Hopf theorem 62 Point transformation 295 Polar spaces 246—248 Principal curvatures 39 Principal framing 42 Principal symbol 145 Projective differential invariants in coordinates 108 Projective second fundamental form 77 Projective second fundamental form, coordinate description of 81 Projective second fundamental form, frame definition of 79 Projective structure 286 Prolongation 147 177 214 220 Prolongation of a G-structure 281 Prolongation property 97 Prolongation property, strict 105 Prolongation structures 233 Pseudospherical surfaces 226—227 Pseudospherical surfaces of revolution 227 Pseudospherical surfaces, Baecklund transformation for 237 Pullback 337 Pushforward 337 Rank of a Lie algebra 327 Rank of a Pfaffian system 341 Rank of a tensor 313 Rational homogeneous variety 83 Reductive Lie group/Lie algebra 327 Refined third fundamental form 129 Regular curve 13 Regular second-order PDB 174 Relative tangent star 131 Representation of Lie algebra 320 Representation of Lie group 316 Representation, isotropy 16 Restraining manifold 255 Retracting space 209 Ricci curvature 53 262 Riemann curvature tensor 52—55 273 Riemann invariant 217 Riemann surface 346 Riemannian geometry 271—273 Riemannian geometry, fundamental lemma 50—51 273 Riemannian manifold 47 Riemannian manifold, flat 52 Riemannian metric 46 47 Right action 15 Root 328 Root system 328 Ruled surface 41 Ruled variety 113 S-structure 309 Scalar curvature 53 262 266 330 Schur's lemma 317 Schwarzian derivative 22 Secant defect 129 Secant variety 86 Second fundamental form, base locus of 80 Second fundamental form, Euclidean 46 Second fundamental form, projective 77 Second-order PDE, characteristic variety 182 Second-order PDE, classical notation 174 Second-order PDE, tableau 175 Section of vector bundle 335 Sectional curvature 53 Segre product of varieties 84 Segre product of varieties, fundamental forms of 101 Segre variety 84 159 Segre variety, fundamental forms of 100 Semi-basic form 339 Semi-Riemannian manifold 274 Semi-simple Lie algebra 327 Severi variety 102 Severi variety, fundamental form of 103 Severi variety, Zak's theorem on 128 Signature of quadratic form 322 Simple Lie algebra 327 Sine-Gordon equation 223 226 235 Singloc 80 Singular locus of 80 Singular solutions 191 SL(V), 317 SO(V,Q), special orthogonal group 317 Space form 57 Space form, isometric immersions of 194 Special Lagrangian submanifolds 200 265 Special linear group 317 Special orthogonal group 317 Special unitary group 319 Spencer cohomology 180 Spin representation 106 107 Spinor variety 85 106 Stabilizer type 282 SU(n), special unitary group 319 Submanifold, associative 265 Submanifold, Lagrangian 185 264 Submanifold, special Lagrangian 200 265 Surface of revolution 41 227 Surface, Bonnet 44 Surface, catenoid 43 Surface, cone 44 Surface, constant mean curvature 229—231 Surface, cylinder 44 Surface, developable 40 Surface, flat 41 Surface, focal 237 266 Surface, helicoid 39 Surface, isothermal coordinates on 57 Surface, linear Weingarten 183 224 261 Surface, minimal 68 228 Surface, parallel 225 Surface, pseudospherical 226 Surface, ruled 41 Surface, warp of 4 Surface, with degenerate Gauss image 91 Symbol mapping 157 Symbol relations 145 174 Symmetric connection 285 Symmetric Lie algebra 291 Symmetric space 290 Symmetries 241 Symplectic form 32 185 199 212 264 317 Symplectic group 317 Symplectic manifold 31 T*M, cotangent bundle 335 Tableau 145 Tableau of linear Pfaffian system 174 Tableau of order p 147
Реклама
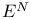, fundamental theorem for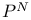 
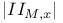
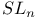, special linear group 
|
|
О проекте