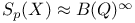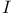|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Mill J.V. — The Infinite-Dimensional Topology of Function Spaces |
|
|
 |
| Предметный указатель |
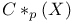 368 371 394 396—399 418 421 425 426 445 590 591 368 371 394 396—399 418 421 425 426 445 590 591
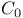 8 354 360 435 436 8 354 360 435 436
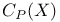 4 368—375 377—379 383—387 393—399 402—404 406 407 409—415 425—428 441 442 444—447 452 455 456 590—592 4 368—375 377—379 383—387 393—399 402—404 406 407 409—415 425—428 441 442 444—447 452 455 456 590—592
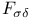 377 442 445 446 518 592 377 442 445 446 518 592
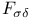 , absolute 344 518—520 , absolute 344 518—520
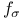 87 227 230 371 466 517 518 522 595 87 227 230 371 466 517 518 522 595
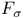 , absolute 518 , absolute 518
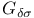 518 518
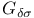 , absolute 344 518—520 , absolute 344 518—520
 35 172 175 217 220 221 229 231 238 257 373 375 127 428 434 454 464 466 467 480 483 485 493 494 517 526 590 35 172 175 217 220 221 229 231 238 257 373 375 127 428 434 454 464 466 467 480 483 485 493 494 517 526 590
 , absolute 518 , absolute 518
 , enlargement 175 304 , enlargement 175 304
 , selection 217 , selection 217
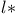 -equivalent 370 418 419 421 425 456 -equivalent 370 418 419 421 425 456
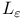 -enlargement 189 -enlargement 189
 -multiplicative 517 522 -multiplicative 517 522
 -operation 594 -operation 594
 -ultrafilter 495 496 -ultrafilter 495 496
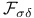 -absorber 350 353 360 361 442 444 -absorber 350 353 360 361 442 444
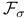 -absorber 347 350 361 -absorber 347 350 361
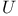 -close 263 -close 263
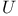 -map 135 136 166 169 176 -map 135 136 166 169 176
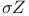 -set 307 334 361 436 441 -set 307 334 361 436 441
 257 257
 -addilive 517 522 -addilive 517 522
 -algebra 455 458 531 -algebra 455 458 531
 -compact 58 66 226 228 339 347 361 411 412 426 479 518 519 581 -compact 58 66 226 228 339 347 361 411 412 426 479 518 519 581
 -compact, nowhere 581 -compact, nowhere 581
 -discrete 369 -discrete 369
 -map 34 66 67 90 135 -map 34 66 67 90 135
Aarts 584 587 594 597
Absolute (Neighborhood) Extensor 25
Absolute neighborhood retract 24—29 38 39 124 145 148 263—265 270 274 276 284 288 289 301—305 580 581 588
Absolute Neighborhood Retract, pair 266 267 273 276 277 285 290 301 304 305 588
Absolute retract 24—27 29 39 145 276 288 289 294 301 305 580
Absolute Retract, hyperspace 292 588
Absolute Retract, pair 266 288 290
Absolute Retract, pair, hyperspace 292
Absolute value 512
Absorber 347 348 589
Absorber Bestvina — Mogilski type 434 589 590
Absorber Dijkstra — van Mill — Mogilski type 347
Absorbing sequence 347 348
Absorbing system 346 347
Accumulation point 462
Addition theorem 178
Adjan 587 597
Adjunction space 507 508
Affine combination 111 114
Affine coordinates 114 125 126 134
Affine function 112—114
Affine function, continuous 113
Affine hull 111
Affine subspace 111—113 124
Alexandroff 253 254 582 584 587 593 597
Alexandroff compactification 472
Alexandroff problem 253 254 587
Almost zero-dimensional 167 168 189 192 583
Analytic set see set analytic
Anderson 9 325 579 580 584 585 588—590 597 598
Anderson Theorem 9 579 588
Antipodal map 148 238 461
Antipodal points 149 461
Antipodal, preserving 149
Approximation Theorem Brown 90
Approximation Theorem Freudenthal 137
Arens 396 579 598
Arhangel'skii 367 372 411 426 451 590 591 598 603
Arveson 455 598
Aull 579 598
Baars x 367 411 425 434 591 592
Baire category theorem 482
Baire space 3 36 66 78 79 373 378 379 383—385 387 391 392 446 482—485 526 580 591—593
Baire space, hereditary 393 446
Baire space, not topologically complete 4&4
Ball, closed 459
Ball, open 459
Banach 579 598
Banach space 3 4 9 10 12 17 21 370 394 579
Banakh 426 437 445 588 590 598
Bandt 594 598
Barit 589 598
Barov x
Bartle 579 598
Barycenter 125 126 128 129 138 139
Barycentric subdivision 129—132
Barycentric triangulation 129 130
Base 41 64 122 153 167 177 238 239 285 288 369 465 467 497 507
Base, closed sets 494 497
Base, collection of sets 441
Base, countable 593
Base, Ellentuck topology 250 251
Base, hyperspace 101
Base, inverse limit 81
Base, local 19 183 368 467 468
Base, Wallman 93 185 494—500
Basic core set 342 343
Becker 49 580 598
Bendixson 592
Bennett 580 598
Berney 593 594 599
Bernstein set 580
Bessaga 371 588 589 599
Bestvina 434 588—590 599
bing 215 580 585 589 593 597 599
Bing compactum 210 212—215
Bing Shrinking Criterion 67 580
Blaszczyk 586 599
Blumenthal 579 599
Bonding map 80 84 93
Borel 594
Borel complexity 445 590
Borel set 80 373 455 456 517—519 523 526 586 590 595
Borel set, absolute 18 437 456 526 592
Borel set, homogeneous 581
Borel set, rigid 581
Borsuk 301 580 581 583 585—588 599
Borsuk Antipodal Theorem 149
Borsuk Example 301 .380
Borsuk Homotopy Extension Theorem 38
Borsuk Homotopy Extension Theorem, controlled 265
Borsuk Problem 588
Borsuk — Ulam theorem 149 174
Boundary 20 125 196 460 464
Boundary, geometric 114
Boundary, preserving homeomorphism 311
Boundary, set 589
Bounded component 505
Bounded function 29 174 368 445
Bounded metric 459 463
Bounded set in a normed linear space 3 7 20 21
Bounded subspace 407 410 417 478
Bourbaki 585 593 599
Bowers 586 588 599 600
Brouwer 221—223 580 582 600
Brouwer 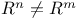 166 166
Brouwer Dimensionsgrad 221
Brouwer fixed-point theorem 143 145 148 149 260 587 594
Brouwer Invariance of Domain Theorem 197
Brown 579 600
Burckol 594 600
C(X) 4 5 19 20 31 368 370—372 393 394 418
C-imbedded 410
Calbrix 446 590 592 600
Cantor 580 592 600
Cantor set 42—48 75 176 229 238 254 257 387 388 434 436 581
Cantor — Bendixson Theorem 467
Cantor-manifold 207 208
Capset 329—331 333 334 337 338 341—343 347 354 589
Carrier 119 134 284
| Cauchy sequence 4 33 58 96 464 468 469
Cauty 24 26 264 367 414 426 445 446 456 580 583 590 592 598 600
Cauty Examples see Example(s) Cauty
Cech 583 584 600
Cech — Stone compactification 368 590
Centered 495
Centered, maximal 495
Chapman 588 589 597 600
Characterization, 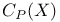 Baire 379 Baire 379
Characterization, 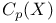 metrizable 369 metrizable 369
Characterization, 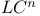 296 298 296 298
Characterization, 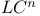 and and  300 300
Characterization, 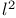 -manifold 588 -manifold 588
Characterization, 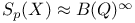 444 444
Characterization, 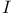 51 51
Characterization, 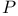 76 77 76 77
Characterization,  76 76
Characterization, A(N)R-pair 267 277
Characterization, absolute 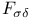 519 519
Characterization, analytic set 77
Characterization, ANR 284
Characterization, AR 39 289
Characterization, boundary point 196
Characterization, Cantor set 43
Characterization, Capset 334 337 590
Characterization, Compact 46O
Characterization, dimension 160 166 174 182 195
Characterization, finite dimensional manifold 588
Characterization, hereditarily 94
Characterization, homogeneous Borel set 77
Characterization, indecomposable continuum 86
Characterization, inessential map 514
Characterization, meager filter 389 434
Characterization, Menger manifold 588
Characterization, Q 294
Characterization, Q-manifold 588 589
Characterization, topologically complete 450
Characterization, zero-dimensional 58 581
Chatyrko 587 600
Chigogidze 588 600 603
Choquct 384 601
Christensen 426 601
Class of spaces, closed hereditary 344
Class of spaces, topological 344
Clopen 41 50 57 58 63 443 460 500
Closed ball 459
Closed base 494
Closed map see map closed
Closed shrinking 485
Closure 460
Coanalytic set 594
Cohen 384 601
COLOR 187
Color number 250
Color, open 251
Color, open or closed 251
Colorable 188
Coloring 187 188 238 241 242 244 245 248 249 251 586
Combinatorially equivalent 123
Comfort 590 592 601
Compact-open topology 19 20 31
Compactification 57 64 87 93 174 182—184 188 193 207 234 253 257 472 473 478 500 510 516
Compactification, Alexandroff 472
Compactification, Cech — Stone 368 590
Compactification, dimension preserving 183
Compactification, equivalent 472
Compactification, one-point 472
Compactification, remainder 183
Compactification, Wallman 93 185 494 498 499 593
Compactness, deficiency 183 204
Compactness, degree 182 183
Compactum Bing see Bing compactum
Compactum Henderson see Henderson compactum
Complete with respect to a norm 16
Complete, metric see metric complete
Complete, topologically see topologically complete
Completely Ramsey set 239
Complex conjugate 512
Component 37 156 167 204 209 285 467 500 501 505 507
Component path 503
Composant 87 94
Cone 21 39 70 89 302 515 516 581
Connected 54 55 57 58 64 85 102 156 206 207 209 473 503—505
Connected in dimension n 295
Connected, locally see locally connected
Connected, path see path-connected
Continuous image, 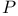 77 77
Continuous image, C 46
Continuous image, complete space 522
Continuous image, Menger curve 585
Continuous image, one-dimensional space 203
Continuous image, zero-dimensional space 57 58
Continuous logarithm 513
Continuum 37 51 58 85 94 95 105 176 209 210 216 261 501 502 505 515 581 593
Continuum Hypothesis 47 384 393
Continuum, 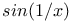 29 57 503 505 517 29 57 503 505 517
Continuum, cook 447
Continuum, decomposable 86
Continuum, from A to B 206 504
Continuum, hereditarily indecomposable 87 94 106 108 212 213 258 260 587
Continuum, hereditarily indecomposable, homogeneous 215 216
Continuum, indecomposable 86 87
Continuum, indecomposable, homogeneous 215
Continuum, Peano 58 226 292 294 295 300 340 585 588
Continuum, unicoherent 226 514
Continuum-connected 206 207 209
Contractible 29 39 70 146—148 274 285 289 301 511 512 515 516 580
Contractible, locally see locally contractible
Contraction 511
Convex 1 2 15 16 19 20 23 25 29 124 125 148 288 581 582
Convex, combination 1 2
Convex, hull 1
Convex, metric 477 479 588
Cook 447 601
Coordinate, functions of a simplex 114
Coordinate, space of inverse sequence 80
Countable closed sum theorem 163
Countable dense homogeneous 63—66 580
Countable dense homogeneous, not homogeneous 63
Countable, dimensional 155 156 221 252 253 428
Countably, compact 473
Countably, continuous 257
Cover 458
Cover, locally finite 486
Cover, refinement 458
Cover, star-finite 135 136
Cover, star-refinement 460
Covering dimension 152 160 583
Criterion, Bing Shrinking 67
Criterion, Inductive Convergence 59 65 325
Curtis 291 325 580 584 588—590 598 601
Curtis — Schori — West Hyperspace Theorem 291 295
Cut 222 504
Cut point 51 504 505
Cut, need not be a partition 221 505
Daverman 588 594 601
de Bruijn 586 600
de Groot, ,J. 373 580 581 584 603 604
de Groot, J.A.M. 367 411 591 592 598
de Vries x 582 612
Decomposable continuum 86
Deformation 510
Deformation property 334 337 343
Deformation through a subset 266—268 276 294 327 355 360 361
Degree compactness 182 183
Degree partition 153
Dellacherie 610
Derivative 417
Derived set 417
Descriptive complexity 373—375 377 446 590
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



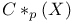
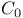
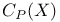
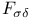
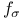
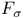 , absolute
, absolute 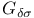

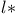 -equivalent
-equivalent 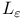 -enlargement
-enlargement  -multiplicative
-multiplicative  -operation
-operation  -ultrafilter
-ultrafilter 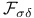 -absorber
-absorber 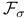 -absorber
-absorber 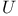 -close
-close 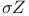 -set
-set 
 -addilive
-addilive  -map
-map 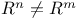
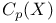 metrizable
metrizable 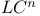

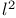 -manifold
-manifold