|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Mill J.V. — The Infinite-Dimensional Topology of Function Spaces |
|
|
 |
| Предметный указатель |
Lemma,  -system 592 -system 592
Lemma, Disjoint Refinement 453
Lemma, Kuratowski — Zorn 18 459
Length of a sequence 46
Level, homotopy 70 510
Level, preserving 71
Level, Whitney 105 106 108 109 258
Levi 594 606
Levin 582—585 587 603 606 607
Lewis 582 607
Lexicographic order 216
Limited by a cover 65 263 265 267
Lindenstrauss 579 607
Linear function 12 17 20 21
Linear homeomorphism 12 21 370 398 403 411 450
Linear hull 111
Linear order 126 216
Linear space 29
Linear space, incomplete 589
Linear space, not ANR 264 580
Linear space, not locally convex 20
Linear space, unit sphere 20
Linear subspace 20
Linear, space 1—4 8 10 12 15—21 26 29 111 114 116 123 130 131 148 197 252 288 361 363 364 369 402 435 452
Linearly, homeomorphic 369 370 398 403 404 447 450
Linearly, independent 5 7 18 20 112
Lipschitz function 99 490
Lipscomb 586 607
Local base 19 183 368 467 468
Locally compact 58 64 87 121 425 456 473 478 482
Locally compact, nowhere 57 58 76
Locally connected 55—58 86 102 222 224 226 285 288 467 505 516
Locally connected in dimension n 296
Locally contractible 28 296 301 516
Locally contractible at a point 516
Locally convex 2 18 19 23—25 29 288 402 452 583
Locally convex 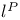 is not 20 is not 20
Locally finite 22 108 136 138 157 158 160 486 487 490
Locally finite, simplicial complex 118 121 125 273 277 284
Locally homotopy negligible 263 588
Locally, path-connected 29 503 504
Locally, uncountable 568
Lowen 579 598
Lower semi-continuous 404 406 488
Lower semi-continuous, set-valued function 13
Lusin 587
Lusternik 583 607
Lusternik — Schnirelman — Borsuk Theorem 148 149 174 586
Lutzer 367 446 456 590—592 601 607
Map, 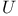 169 169
Map,  34 66 67 90 135 34 66 67 90 135
Map, closed 109 241 460 464 467
Map, closed, dimension raising 199
Map, essential 512
Map, inessential 512
Map, irreducible 477
Map, linear see linear function
Map, monotone 504
Map, open 107 108 464 477
Map, quotient 108 505 506 508 509
Map, Sperner 141
Map, Whitney 103—106 108 109 258
Marciszcwski ix x 18 367 393 398 414 426 434 445—447 456 588 590—593 600 601 607
Mardesic 588 607
Martin 610
Mauldin 587 605
Mazur 586
Mazurkiewicz 580 582 585 586 594 605 607
Mazurkiewicz Theorem 55
McCoy 367 590 591 607
Meager 66 87 447 449 483 520 522 526
Meager at a point 526
Meager filter 389—391 434 436
Meager, collection of sets 389
Menger 234 583—585 605 607
Mesh collection 459
Mesh simplicial complex 130
Mesh subdivision 130 131
Metric 30 90 361 363 463 464 478 484
Metric, admissible 460
Metric, bounded 459 463
Metric, complete 3 21 33 35 58 96 98 463 474 477 479 480 485
Metric, convex 108 477 479 588 593
Metric, derived from a norm 2 3
Metric, Euclidean 3
Metric, Hausdorff 95 96 106 107
Metric, Nagata 586
Metric, non-Archimedean 57 58
Metric, nonconvex 325
Metric, s 19
Metric, totally bounded 96 98 479 484
Metrization Theorem, Nagata — Smirnov — Bing 593
Metrization Theorem, Urysohn 465 593
Michael 396 452 579 607 608
Michalewski x 591 608
Miljutin 370 608
Miljutin Theorem 370
Miller 517 581 595 603 608
Mogilski ix 367 434 588—592 599 601 608
Moise 593 608
Monger compacta 588
Monger curve 583 585
Monotone map 504
Moore 59—51 608
Morita 584 609
Moschovakis 517 609
Mostowski 517 594 606
Moszyriska 588 609
Mrowka 584 609
multi-valued function 404
Munkres 582 609
Nadler 582 605 609
Nagami 584 609
Nagata 372 457 582 586 593 609
Nagata — Smirnov — Bing Theorem 593
Natural numbers 457
Near homeomorphism 66 67 70 90 94
Negrepontis 590 592 601
Neighborhood retract 512
Nerve 132 133
Net 484
Nhu 588 590 601
Nikodym 594 609
Nishiura 584 597 604
Nobeling 583 609
Nodec space 385
Noebeling's universal space 168 172 174
Norm 2 3 579
Norm, Euclidean 3
Normal set, in the sense of Frechet 221
Novikov 587 597
Nowhere,  -compact 581 -compact 581
Nowhere, countable 581
Nowhere, dense 86 197 387 388 436
Nowhere, locally compact 57 08 76
Nowhere, topologically complete 581
Ntantu 367 591 607
Null-sequence 508
Nullhomotopic 145 148 149 204 300 510 511 514
Okunev 426 609
Olszewski 586 609
Open ball 459
Open Ellentuck topology 240
Open map 10 57 107 108 460 464 477
Open problem see problem open
Open, shrinking 485
Open, swelling 157 158
Order cover 160
Order, lexicographic 216
Order, linear 126 216
| Order, preserving indexed collection 344
Origin of Q 4 61
Otto 583 602
Oversteegen 583 584 609
Oxtoby 384 593 609
P-point 393 446
Page 579 600
Paracompact 125 369 396 487 490
Parthasarathy 585 609
Partial realization 270 273 281 282 284 296
Partition 1—16 153—155 157 175 179 182 193 206 209 221 252 504 505
Partition space 125 443 509
Partition unity 487 488
Partition,  80 80
Partition, Bing 210 213
Partition, continuum 502
Partition, cut is 222
Partition, degree 153
Partition, irreducible 155 157 193 226
Path 503
Path-component 503
Path-connected 29 55 57 58 94 285 503—505 511
Path-connected locally 29 57 503 504
Pavlovskii 591 609
Peano 580
Peano continuum see continuum Peano
Peano map 580
Pelant 591 592 598 607 609
Perfectly disconnected 385 592
Pestov 591 609
Petezyriski 371 579 588 589 599 609
Poincarc 221 583 609
Point, accumulation 462
Point, cut 51
Point, P 393 416
Point, weak P 386
Pointwise convergence topology see topology pointwise
Pol Examples 447 450 587
Pol, E. 587 600 609
Pol, R. x. 220 384 446 447 456 580 583—587 590 592 602—604 606—610
Polyhedron 124 136 274 310 588
Polytope 123 132 136 166 270 274 276 304
Pontrjagin 583 584 603 610
Power set 458
Prikry 586 603
Problem, Alexandroff 253 254 587
Problem, Anderson — Bing 589
Problem, Banach and Frechet 579
Problem, de Groot 584
Problem, open 145 161 216 236 260 404 414 '125 446 447 580 581 587 592
Problem, Schauder 582
PRODUCT 26 41 58 82 235 339 368 371 450 461 467 480 516 519
Product, cartesian 457
Product, Cartesian, weak 355
Projection 70 81 84 398 457 477 478
Property of Baire 434 520—523 594
Property, closed hereditary 84
Property, countably productive 84
Property, fixed-point 92 145 146 148 516
Przymusinski 583 610
Pseudo arc 215
Pseudo boundary 60
Pseudo interior 60
Punctiform 221
Pytkeev 591 610
Q-set 595
Quinn 589 610
Quotient map 108 505 506 508 509
Quotient topology 398 505 506 509
Quotient topology, not metrizable 509
Radul 437 588 590 598
Ramsey set 239
Ramsey set, completely 239 240
Ramsey theory 238 240
Rational numbers 42 58 76 78—80 182 384 416 457 483 494 517 519 520 581 594
Rational numbers, not topologically complete 483
Real numbers 457
Realization, full 270 273 277 284 296
Realization, geometric 116
Realization, partial see partial realization
Reed 612
refinement 160 166 176 263 273 277 284 296 458
Refinement, disjoint 41 168 453 463
Refinement, star 272 460
Refinement, star-finite 136 166 272
Reflexively universal 345
Repovs 579 610
retract 146 148 276 512 516 517
Retract neighborhood 26 512
Retraction 512
Rigid space 447 581
Rogers 455 610
Rogers, Jr. 216 587 606 610
Roy 584 610
Rubin 585 587 590 602 610
Rudin, W. 393 610
S 3 9 19 20 26 60 66 257 310 311 314 319 320 322—324 339 342 343 364 579 587 588
Salomon x
Scattered 417 419 456
Scattered height 418
Schauder 582 610
Schauder fixed-point theorem 148 583
Schnirehnan 583 607
Schori 291 581 585 588 601 610
Segal 584 588 606 607
Segment, initial 46
Segment, straight-line 19
Seirienov 579 610
Selection 13 29
Selection,  217 217
Selection, continuous 13 16
Semadeni 394 451 603
Semi-continuous, lower 13 406 488
Semi-continuous, upper 257 489
Separated 1^91
Separating set 148
Separator 504
Sequence functions 4®9
Sequence homeomorphisms 59 65
Sequence, 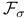 -absorbirig 352 -absorbirig 352
Sequence, absorbing 350
Sequence, compacta 478
Sequence, inverse see inverse sequence
Sequence, null 58 508 509
Sequentially compact 473 474
Set, 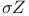 see see 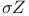 -set -set
Set, analytic 48 49 77 435 436 439 441 455 522 523 526 590 594
Set, Borel see. Borel set
Set, Cantor see Cantor set
Set, coanalytic 594
Set, derived 417
Set, meager 483
Set, power 458
Set, property of Baire 434 520—523 594
Set, Ramsey see. Ramsey set
Set, scattered 417
Set, Z see Z-set
Set-valued function 12
Shchepin 585 603
Shelah 393 581 610
Sher 589 610
Shift, 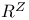 587 587
Shift, inverse limit 91 92 249
Shrinkable 66—68 70
Shrinking 159 160 167 244 485 486
Shrinking, closed 185
Shrinking, open 485
Sierpinski 580—582 585—587 592 594 611
Sierpiriski Carpet 583
Sierpiriski Theorem 502
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -system
-system 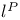 is not
is not 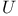

 -compact
-compact

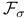 -absorbirig
-absorbirig