|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Mill J.V. — The Infinite-Dimensional Topology of Function Spaces |
|
|
 |
| Предметный указатель |
Sikorski 384 611
Simple chain 54
simplex 114 124
Simplex, full 141
Simplex, geometric 114
Simplex, n-dimensional 114
Simplicial complex 116 117
Simplicial complex, locally finite 118
Simplicially homeomorphic 123
Sin(1/x)-continuum 29 57 503 505 517
Skeleton 117 122 271
Smirnov 593
Sokolov 393 604
Solenoid, dyadic 85
Solenoid, p-adic 581
Souslin 580 594 611
Space 465
Space filling curve 46
Space, adjunction 507 508
Space, Baire see Baire space
Space, Banach see Banach space
Space, Euclidean 3 64 151 461
Space, infinite-dimensional compacta 350
Space, linear see linear space
Space, normal 121
Space, perfectly disconnected 385 592
Space, rigid 447 581
Space, scattered 417
Space, topological 465
Space, Tychonoff 367
Spanier 582 611
Sperner 582 611
Sperner Lemma 141
Sperner map 141
Sphere 3 9 20 26 29 63 85 92 146—149 194—196 201 204 207 226 288 291 297 310 461 473 511 516
Spiez 605
Square 87 89 93 384 450
Standard simplex 539
Standard triangulation 117 139
Star 119 460
Star refinement 272 460
Star, finite 135 138 166
Stciner, A.K. 591 611
Steel 581 603
Steenrod 593 602
Steiner, E.F. 594 611
Steinlein 245 586 611
Sternfeld 582 586 587 606 607 611
Stone 369 610 611
Straight-line segment 19
Straight-line segment, parametrization 361
Strong local homogeneity 64 73 75 580
Strongly discrete family 377- 379
Strongly homogeneous 75
Strongly infinite-dimensional see dimension strong
Subbase 19 31
Subcomplex 117
Subpolyhedron 124
Subpolytope 124
Subspace Theorem 164
SUM 371
Sup-norm 4
Support 404—407
Support homeomorphism 64
Swelling 157 158
Symmetric difference 457
t*-equh'alent 426 -156
t-equivalent 371 414 426 428 445 456 591 592
Taimanov 593 611
Talagrand 591
Taylor 579 611
Theorem Addition 178
Theorem Anderson 9 579 588
Theorem Borsuk 149
Theorem Borsuk — Ulam 149 174
Theorem Brouwer 143 145 148 149 157 260 587 594
Theorem Brown 90
Theorem Cantor — Bendixson 467
Theorem Cauty 24 583
Theorem Chapman 588
Theorem Closed Graph 12
Theorem Coincidence of Dimension Functions 180
Theorem Countable Closed Sum 163
Theorem Curtis — Schori — West 291
Theorem Dobrowolski — Marciszewski — Mogilski 444
Theorem Dugundji 23 29 394 451 588
Theorem Freudenthal 137
Theorem Galvin — Prikry 586
Theorem Jordan 174
Theorem Keller 581
Theorem Kuratowski — Wojdyslawski 19
Theorem Lavrentieff 493
Theorem Lusternik — Schnirelman — Borsuk 149 174
Theorem Marciszewski 398 447
Theorem Mazurkiewicz 55
Theorem Michael 16
Theorem Miljutin 370
Theorem Nagata — Smirnov — Bing 593
Theorem Pol 254
Theorem Schaudcr 148 583
Theorem Sierpiriski 502
Theorem Souslin 47
Theorem Sperner 141
Theorem Subspace 164
Theorem Tietze 24
Theorem Toruriczyk 291 294 588 589
Theorem Urysohn 465
Theorem van Douwen 48
Theorem van Engelen 581
Theorem West 588
Tietze 593 611
Tkachuk 591 611
Tolstowa 583 610
Tomaszewski 586 611
Topological group 1 37 60 182 215 462
Topological group 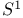 85 85
Topological group 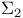 85 85
Topological group homeomorphisms 35—37 583
Topological group Q is not 60
Topological group, homogeneous 464
Topological property, closed hereditary 84
Topological property, countably productive 84
Topological space 465
Topologically complete 47—49 55 57 65 66 76 77 183 222 226 480 482 484 493 518 519 522 523 526 581 594
Topologically complete, 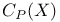 415 415
Topologically complete, 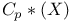 591 591
| Topologically complete, 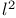 9 9
Topologically complete, 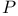 482 482
Topologically complete,  is not 483 517 is not 483 517
Topologically complete, 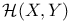 35 35
Topologically complete, A(N)R enlargement 305
Topologically complete, Baire 482
Topologically complete, C(X,Y) 33
Topologically complete, compactification 253
Topologically complete, Continuum Hypothesis 47
Topologically complete, dense subspace 484 526
Topologically complete, dimension 220 224 584
Topologically complete, hyperspace 98
Topologically complete, inverse limit 84
Topologically complete, nowhere 581
Topologically complete, topological sum 484
Topologically complete, totally disconnected 183 218 221
Topologically complete, weakly n-dimensional 231
Topology, compact-open 19 20 31
Topology, coordinatewise convergence 9 467
Topology, euclidean 19 20
Topology, pointvvise convergence 4 368 372
Topology, quotient see quotient topology
Topology, Tychonoff product 368
Topology, uniform convergence 7 31
Topology, Vietoris 101 108 582
Topology, weak 354
Topology, Whitehead 118 119 132
Topsoe 610
Torubczyk Theorems 291 294 588
Toruriczyk 263 291 294 580 588 605 611
Totally disconnected 50 58 167 183 218 221
Tower 337
Tower, deformation property 334 343
Tower, expansive 331
Translation 462
Triangulation 117
Triangulation, standard 117
Trivial homotopy class 511
Tumarkin 583—585 611 612
Tychonoff product topology 368
Tychonoff space 367
Tymchatyn 583 584 609
Type homotopy 276
Type of a point 63
Tzafriri 579 607
Ul'janov 593 612
Ultrafilter 391—393 459 462 463 495 496
Unbounded component 505
Unicoherent 204 226 514 515
Uniformly continuous 477 448
UNION operator 99
Unit ball 3
Unit ball,  3 461 3 461
Unit interval 457
Unit sphere 3
Unit sphere,  3 461 3 461
Universal 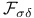 439 439
Universal 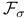 354 354
Universal 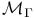 344 345 344 345
Universal curve 583 585
Universal reflexively 345 350 355 364 439
Universal space, compact 176
Universal space, Noebeling 168 172 174
Universal space, weakly n.-dimensional 232
Universal strongly 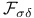 361 361
Universal strongly 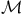 348 361 348 361
Universal strongly 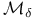 348 348
Universal strongly 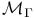 344 346 344 346
Upper semi-continuous 257 489
Upper semi-continuous decomposition 106 501 505—509
Urysohn 222 580 581 583—585 593 594 597 612
Urysohn function 469
Urysohn Metrization Theorem 465 593
Uspenskii 585
Ustinov 611
Usual topology on ![$[\mathbb{N}]^{\omega}$](/math_tex/908a36fc841e157a11748f4942cbf8ca82.gif) 239 239
Valdivia 384 600
van Dantzig 582 601
van de Vel 580
van der Bijl 588 599
van Douwen 75 384 580—583 586 591—594 602
van Engelen 49 580 581 594 598 602 603
van Hartskamp, x 587 604
van Mill 9 49 64 294 325 367 384 426 434 445—447 456 580—582 584—592 598 601—604 607 608 612
Vaughan 608
Vermeer 586 587 597 604
Vertex 116—118 280
Vietoris 582 612
Vietoris topology 101 108 582
von Neumann 455
Wallman 222 584 585 593 605 612
Wallman base 93 185 494—500
Wallman compactification 93 185 494 498 499 593
Walsh 585 587—589 599 604 610 612
Warsaw circle 301
Warsaw circle, homotopically trivial 285
Wazewski 582 612
Weak Cartesian product 355
Weak P-point 386
Weak topology 354 465
Weakly infinite-dimensional 251 252 254 257
Weakly infinite-dimensional, not countable dimensional 254
Weakly n-dimensional 228 231 586
Weakly n-dimensional, universal 232
Weakly one-dimensional 235
Weight 369
West 291 588 589 610 612
Whitehead 132 612
Whitehead topology 118 119 132
Whitehead torsion 588
Whitney 582 612
Whitney level 105 106 108 109 258
Whitney map 103—106 108 109 258
Wille 581 604
Wimmers 393 612
Wojdyslawski 579 588 612
Wong 589 610
Yankov 455
Z-imbedding 327 328 338 343 360 361
Z-Map 327
Z-set 307—311 323—331 333 334 337 338 343 58
Zarelua 585 612
Zarichnyi 437 588 590 598
zero-dimensional 41—45 57 58 73 75 76 153 154 157 165 174 177 178 182 210 230 241 253 425 581
Zero-dimensional, almost 167 168 189 192 583
Zorn 80
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



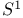
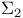
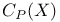
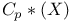
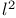
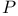
 is not
is not 

![$[\mathbb{N}]^{\omega}$](/math_tex/908a36fc841e157a11748f4942cbf8ca82.gif)