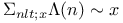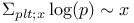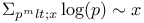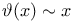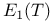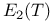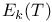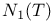|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Borwein P., Choi S., Rooney B. — The Riemann Hypothesis |
|
|
 |
| Предметный указатель |
Series representation, 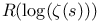 16 16
Series representation, 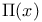 406 410 406 410
Series representation, 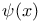 325 408 463 465 485 325 408 463 465 485
Series representation, 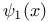 409 409
Series representation, 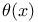 321 321
Series representation, 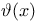 379 392 379 392
Series representation, 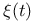 204 204
Series representation,  33 464 33 464
Series representation, 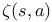 144 144
Series representation, F(X, T) 488
Series representation, L(x) 431
Series representation, Li(x) 98
Series representation, log(n) 469
Series representation, log(s - 1) 224
Series representation, M(x) 69 433 469 471 472 475 477
Series representation, R(t, x) 159
Series representation, S(t, x) 160
Series, 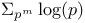
Series, 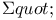 266 278 306 266 278 306
Series,  266 278 305 266 278 305
Series, 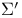 266 278 305 266 278 305
Series,  278 278
Series, 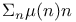 298 480 298 480
Series, 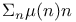 , convergence 298 453 457 , convergence 298 453 457
Series,  214 224 320 322 214 224 320 322
Series,  , convergence 320 , convergence 320
Series, 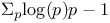 291 291
Series, 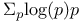 392 399 453 457 472 479 392 399 453 457 472 479
Series, 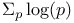 98 289 321 379 392 98 289 321 379 392
Series, 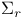 275 275
Series,  339 339
Series, 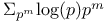 282 290 291 282 290 291
Series,  249—251 249—251
Series, 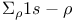 243 254—257 259 260 262 263 266—270 305 306 243 254—257 259 260 262 263 266—270 305 306
Series,  275 275
Series,  407 408 407 408
Series,  407 408 407 408
Series,  245 245
Series,  244 244
Series, 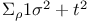 247 248 247 248
Series,  290 290
Series, 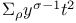 274 275 277 274 275 277
Series, 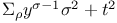 279—281 285 287 289 297 279—281 285 287 289 297
Series,  245 245
Series, Dirichlet 217 219 232 314
Series, Dirichlet, 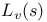 221 221
Series, Dirichlet, sommablilite 314
Series, Farey 48
Series, Farey, 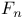 48 48
Series, Meyer 233
Series, nontrivial zeros 23 50 125 128 130 143 245 247—251 266—270 274 278 305 429 431 437 439 440 442 449 488
Series, upper bound 407
Series, Weber 233
Serre 111 114
Set, introspective integers 517
Set, N 514
Set, positive integers 514
Severi 105 335 336
Sherman 375
Shilov 151
Shimura 111
Shimura — Taniyama — Weil conjecture 111
Siegel 32 70 126 133 141 158
Sieve 64 133 475 477 478 512 “Upper
Sieve of Eratosthenes algorithm 511
Sieve of Eratosthenes algorithm, running time 511
Sieve, estimate 489
Sieve, large 475 477
Sieve, prime distribution 477
Sieve, prime number density 512
Sieve, technique 469
Sign, 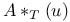 433 435 433 435
Sign, 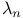 50 50
Sign,  43 142 209 403 405 410 415 418 426 43 142 209 403 405 410 415 418 426
Sign,  , change 405 , change 405
Sign, 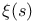 27 27
Sign, 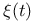 101 101
Sign, 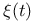 , change 101 102 , change 101 102
Sign, 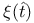 38 38
Sign, 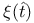 , change 38 , change 38
Sign, 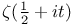 33 33
Sign, 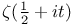 , change 33 , change 33
Sign, change 357 358
Sign, Gauss sum 112
Sign, L(x) 431
Sign, L(x), verification 431
Simple pole,  221 221
Simple pole, 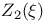 147 147
Simple pole, 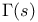 14 14
Simple pole, 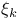 218 218
Simple pole,  11 14 15 97 101 123 139 213 322 342 11 14 15 97 101 123 139 213 322 342
Simple pole, 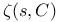 103 103
Simple pole, 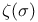 17 17
Simple pole, Z(t, C) 103
Simple zero,  14 38 39 102 141 142 440 14 38 39 102 141 142 440
Simple zero, Z(t) 141
Skewes 43 44 403 405
Skewes number 43
Skewes number, bound 43 44
Skewes number, upper bound 43 44
Snaith 67 115 131 132
Sobolev space 116
Solovay 63 512
Solovay — Strassen algorithm see “Algorithms”
Solovay’s primality testing algorithm 512
Sophie Germain primes 512 520
Sophie Germain primes, asymptotic behavior 520
Sophie Germain primes, density 512 520
Sophie Germain primes, primality test 512 520
Soundararajan 67
Spacing between zeros, 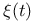 105 105
Spacing between zeros,  41 42 102 125 130 133 134 141 150 437 439 488 498 41 42 102 125 130 133 134 141 150 437 439 488 498
Spacing between zeros,  , average 441 , average 441
Spacing between zeros,  , distribution 443 , distribution 443
Spacing between zeros,  , kth 41 , kth 41
Spacing between zeros,  , normalized 41 , normalized 41
Spacing between zeros,  , small 43 , small 43
Spacing between zeros, 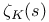 441 441
Spacing between zeros, 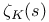 , bound 441 , bound 441
Spacing between zeros, L-function 105 135
Spacing between zeros, Z(t) 142 143 150 157
Spacing between zeros, zeta function 105
Spectral interpretation, zeros, 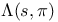 115 115
Spectral interpretation, zeros,  115 127 128 132 115 127 128 132
Spectral interpretation, zeros, L-function 116
Spectral theory 147 149
Spectral theory, non-Euclidean Laplacian 147
Spectrum 128
Spira 144
Steiner 193
Stern 193
Stieltjes 69 125 213 224 225 299
Stirling 21
Stirling’s formula 21 22 26 143 158
Strassen 63 512
Strassen’s primality testing algorithm 512
Subconvex estimate 115
Sudan 518
Sum of divisors function 47 48
Sum of divisors function, Riemann hypothesis 48
Summability 491
Summability, Dirichlet series 314
Support 54
Supremum, 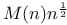 70 70
Supremum, 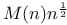 , lower bound 70 , lower bound 70
Supremum, 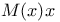 471 471
Supremum, 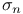 241 258 261 241 258 261
Supremum, zeros, imaginary parts 255 258 441 443
surface 105
Surface, arithmetic hyperbolic 114
| Surface, projective nonsingular 105
Swinnerton — Dyer 134
Sylvester 239
Symmetric functional equation 123 158
Symmetric functional equation,  123 158 123 158
Symmetric group 53
Symmetric group, element 53
Symmetric group, element, order 53
Symmetric matrix 437 442
Symmetric matrix, eigenvalue 437 442
Symplectic matrix 105 132 437 442
Symplectic matrix, eigenvalue 105 437 442
Symplectic matrix, unitary 132
Szele Prize 339
Taniyama 111
Tate 106
Tauberian character 490
Tauberian theorem 327 (see also “Auxiliary Tauberian theorem”)
Tauberian theory 462
Taylor 101
Taylor series 16 26 323 351
Taylor’s Formula 152 159
Tchebotarev’s density theorem 100
Tchebychev 99 225 239 240 455 457
te Riele 44 62 69 70 102 125 141 142 147
Ternary additive divisor problem 149
Terras 129
Theoreme, Bohr 314
Theoreme, Cauchy 313
Theoreme, Halphen 225 231 232
Theoreme, nombres premiers 469 471
Theoreme, nombres premiers, demonstration 471
Theoreme, Riesz 314
Theoreme, von Mangoldt 274 275
Theorems,  67 67
Theorems,  , proof 67 , proof 67
Theorems,  67 67
Theorems,  , proof 67 , proof 67
Theorems,  67 67
Theorems,  , conditional proof 67 , conditional proof 67
Theorems,  , proof 67 , proof 67
Theorems,  67 67
Theorems,  , proof 67 , proof 67
Theorems,  15 19 24 31 41 15 19 24 31 41
Theorems,  , proof 15 24 31 , proof 15 24 31
Theorems,  , von Mangoldt 15 31 , von Mangoldt 15 31
Theorems, $\dfrac1{\Gamma(\mu)}\Sigma_{p<x} \log(p)\log^{\mu-1}\left(\dfrac{x}{p}\right) \sim x 231
Theorems,  43 46 61 98 100 140 142 171 211 235 239—241 296 298 43 46 61 98 100 140 142 171 211 235 239—241 296 298
Theorems,  , proof 211 235 , proof 211 235
Theorems,  16 171 182 320 328 455 461 463 16 171 182 320 328 455 461 463
Theorems,  323 327 463 323 327 463
Theorems,  , proof 331 465 , proof 331 465
Theorems,  480 480
Theorems,  , proof 331 , proof 331
Theorems, 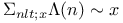 125 325 125 325
Theorems,  379 379
Theorems,  292 392 453 472 479 292 392 453 472 479
Theorems,  , proof 457 458 , proof 457 458
Theorems, 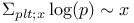 225 231 289 225 231 289
Theorems,  291 291
Theorems, 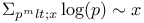 289 289
Theorems, 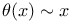 321 321
Theorems, 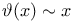 379 381 392 379 381 392
Theorems, M(x) = o(x) 325 327 469 471 475 477
Theorems, M(x) = o(x), proof 330 469 471 475 477 478 480
Time magazine 70
Titchmarsh 58 63 65 66 102 127 133 311 325 417 462 498
Titchmarsh’s S(T) function 65
Trace formula, Selberg 128 129
Trace, Frobenius endomorphism 104
Transcendence of 2, 126
Trivial zero 14 97 124
Trivial zero,  14 139 202 242 322 342 14 139 202 242 322 342
Tsang 150 156
Turan 71 142 339 341 433 478 483 484
Turan — Kubilius inequality 478 483 484
Turan — Kubilius inequality, dual 483 484
Turan — Kubilius inequality, large sieve inequality 478 483 484
Turan’s conjecture 433 524
Turan’s conjecture, conditional disproof 433
Turan’s inequality 433 (see also “Turan’s conjecture”)
Turan’s inequality, conditional disproof 433
Turan’s inequality, disproof 435
Turing 34 514
Turing machine 514
Turing machine, deterministic polynomial time 514
Turing’s algorithm 34
Twin prime constant 520
Twist 132
Twist, quadratic 132
Ungar 343
Ungar’s theorem 343
Unitary linear operator 437 442
Unitary matrix 67 105 129 437 442
Unitary matrix, characteristic polynomial 67
Unitary matrix, eigenvalue 105 129 437 442
Unitary matrix, symplectic 132
Unitary representation, irreducible 112
Upper bound sieve 478
Upper bound sieve, Selberg 478
Upper bound, 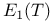 146 146
Upper bound, 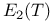 146 146
Upper bound, 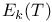 146 148 146 148
Upper bound, 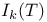 66 66
Upper bound, 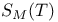 164 164
Upper bound, 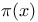 98 99 321 465 98 99 321 465
Upper bound, 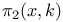 497 497
Upper bound, 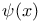 99 408 465 99 408 465
Upper bound,  241 258 261 403 405 406 409 241 258 261 403 405 406 409
Upper bound,  48 48
Upper bound, 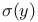 281 282 281 282
Upper bound,  407 407
Upper bound,  407 407
Upper bound, 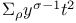 277 278 277 278
Upper bound, 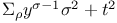 279—281 279—281
Upper bound, 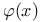 178 178
Upper bound, 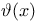 99 380 393 99 380 393
Upper bound, 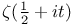 146 146
Upper bound, 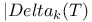 148 148
Upper bound, cardinality of 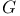 518 518
Upper bound, distribution of zeros 445
Upper bound, infimum, 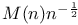 70 70
Upper bound, Li(x) 409 410
Upper bound, M(x) 478
Upper bound, prime distribution 477 478
Upper bound, S(T) 150
Upper bound, Skewes number 43 44
Upper bound, Z(t) 151
Upper bound, zeros, Davenport — Heilbronn zeta function 144
Upper bound, zeros, imaginary parts 449
Vaaler 496
Valeur principale, de Li(x) 240
Value, 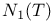 38 38
Value, 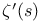 49 49
Value, 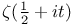 150 150
Value, S(T) 150
van de Lune 102 126 142
Van der Waerden 335
Variety, algebraic 102 103
Variety, arithmetic 100
Variety, field 105
Variety, finite field 105 115
Variety, finite field, Riemann hypothesis 105 115
Variety, general 131
Variety, general, Riemann hypothesis 131
Variety, non-singular 105
Variety, projective 105
Variety, zeta functions 105
Vaughan 487 504
Verdier 103
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



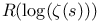
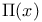
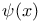
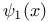
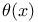
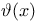
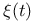

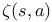
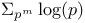
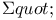

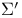

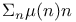

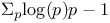
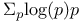
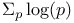
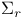

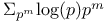

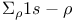





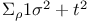

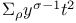
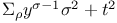

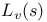
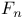
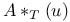
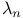

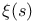
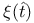
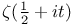

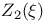
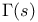
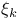
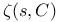
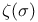
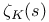
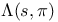
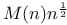
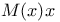
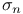









 , proof
, proof