|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Borwein P., Choi S., Rooney B. — The Riemann Hypothesis |
|
|
 |
| Предметный указатель |
Nontrivial zero, 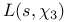 130 130
Nontrivial zero, 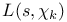 57 57
Nontrivial zero, 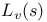 222 222
Nontrivial zero, 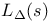 130 130
Nontrivial zero, 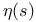 49 49
Nontrivial zero,  127 127
Nontrivial zero,  5 15 18 38—41 70 97 99 125 139—143 165 242—244 247 274 311 313 321 322 342 349 403 405 429 431 437 439 462 485 488 495 5 15 18 38—41 70 97 99 125 139—143 165 242—244 247 274 311 313 321 322 342 349 403 405 429 431 437 439 462 485 488 495
Nontrivial zero,  , ,  241 261 265 270 241 261 265 270
Nontrivial zero,  , ,  241 258 261 241 258 261
Nontrivial zero,  , ,  125 143 242 125 143 242
Nontrivial zero,  , ,  429 431 429 431
Nontrivial zero,  , argument principle 19 , argument principle 19
Nontrivial zero,  , conjugate 243 , conjugate 243
Nontrivial zero,  , counting 18 19 , counting 18 19
Nontrivial zero,  , distribution 440 , distribution 440
Nontrivial zero,  , existence 27 38 42 322 440 , existence 27 38 42 322 440
Nontrivial zero,  , proportion 27 , proportion 27
Nontrivial zero,  , simple 102 , simple 102
Nontrivial zero,  , smallest 35 38 41 70 101 102 139 243 405 416 417 429 431 432 , smallest 35 38 41 70 101 102 139 243 405 416 417 429 431 432
Nontrivial zero,  , symmetric 15 , symmetric 15
Nontrivial zero, 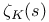 58 58
Nontrivial zero,  111 111
Nontrivial zero, Davenport — Heilbronn zeta function 144
Norm, conjugacy class 145
Norm, divisor 103
Norm, integral ideal 58
NP see “Complexity class”
Number field 58
Number of primes 97 193 201 209
Numerator, 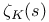 336 336
Numerator, 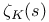 , degree 336 , degree 336
Numerator, 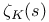 , polynomial 336 , polynomial 336
Numerator, Z(t, C) 103
Nyman 53 127
Nyman — Beurling equivalent form 53
Nyman — Beurling equivalent form, Riemann hypothesis 53
Nyman — Beurling theorem 127
Odlyzko 35 42 51 69 70 102 105 115 116 125 126 131 141 142
Odlyzko — Schonhage algorithm 35
Operator 26
Operator, Hecke 101
Operator, hermitian 40 127
Operator, integral 52
Operator, integral, Hilbert — Schmidt 52
Operator, Laplace 128
Operator, linear 105 437 442
Operator, self-adjoint 115
Orbit 52
Orbit, closed 52
Order see “Multiplicity”
Order,  145 145
Order, 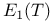 145 145
Order, 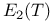 145 147 145 147
Order, 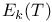 148 148
Order, 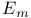 33 33
Order, 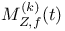 152 152
Order,  165 165
Order,  102 102
Order,  , Ingham’s exponent 102 , Ingham’s exponent 102
Order, 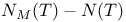 165 165
Order, $S(T)S 66
Order, 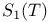 66 66
Order,  321 321
Order, 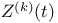 151 151
Order,  241 298 241 298
Order, 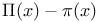 410 410
Order, 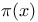 320 321 320 321
Order, 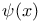 323 323
Order, 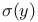 281 282 281 282
Order, 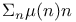 302 302
Order,  277 278 277 278
Order,  279—281 279—281
Order, 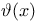 393 393
Order, 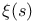 143 143
Order,  , bound 146 , bound 146
Order,  , critical line 146 , critical line 146
Order, 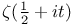 126 146 126 146
Order, group element 53
Order, integer modulo n 514
Order, Li(x) 409
Order, M(x) 69 70 125
Order, R(x) 386
Order, S(T) 125 140
Order, symmetric group element 53
Order, symmetric group element, equivalent statement 54
Order, Z(s) 145
Order, Z(t) 151
Orthogonal matrix 105 132
Orthogonal matrix, eigenvalue 105
Oscillations, of Z(t) 150 151
P see “Complexity class”
Pair correlation 130 134 437 439 442 485 487 488
Pair correlation conjecture 488
Pair correlation function 42 437 442
Pair correlation function, eigenvalue, Gaussian unitary ensemble 42
Pair correlation function, eigenvalue, Hermitian matrix 437 442
Pair correlation function, eigenvalue, unitary matrix 437 442
Pair correlation function, plot 42
Pair correlation, eigenvalue 437
Pair correlation, eigenvalue, symmetric matrix 437 442
Pair correlation, eigenvalue, symplectic matrix 437 442
Pair correlation, Montgomery 502
Pair correlation, prime numbers 485 487 489
Pair correlation, short interval 485 487
Pair correlation, zeros of  42 442 485 487 498 42 442 485 487 498
Parseval 446
Parseval’s identity 446
Partial sum 339 373
Partial sum, 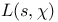 373 373
Partial sum, 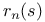 345 345
Partial sum, 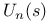 343 347 349 343 347 349
Partial sum, 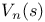 348 366 348 366
Partial sum,  353 353
Partial sum, alternating zeta function 348 (see also “Partial sum
Partial sum, Dirichlet series 351
Partial sum, power series 375
Partial sum, Riemann hypothesis 71 339 343 344 347 348
Partial sum, Riemann zeta function 71 339 343
Partial sum, zero 339 350 351
Partial sum, zero, behavior 345
Partial sum, zero, condensation point 350 351 375
Partial sum, zero-free region 339
Paths,  159 159
Paths,  159 159
Peak 162
Peak,  40 40
Peak, 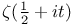 102 102
Peak, Z(t) 150 151
Perfect square 520
petersen 374
Phragmen — Lindelof theorem 126
Piltz 223
Plancherel 502
Plancherel’s identity 502
Poincare 224
Poisson summation 13
Pole, 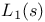 221 221
Pole, 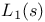 , multiplicity 221 , multiplicity 221
Pole, 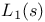 , simple 221 , simple 221
Pole, 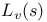 221 221
Pole, 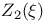 147 147
Pole, 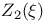 , critical line 147 , critical line 147
Pole, 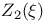 , multiplicity 147 , multiplicity 147
Pole, 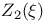 , multiplicity five 147 , multiplicity five 147
Pole, 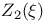 , simple 147 , simple 147
Pole, 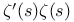 , residue 243 244 , residue 243 244
Pole, 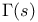 13 14 242 13 14 242
Pole, 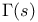 , residue 13 , residue 13
Pole, 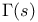 , simple 14 , simple 14
Pole, 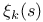 218 218
| Pole, 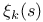 , multiplicity 218 , multiplicity 218
Pole, 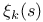 , residue 218 , residue 218
Pole, 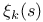 , simple 218 , simple 218
Pole,  11 14 15 38 97 101 123 133 139 202 213 216 322 342 11 14 15 38 97 101 123 133 139 202 213 216 322 342
Pole,  , multiplicity 11 14 , multiplicity 11 14
Pole,  , residue 11 15 , residue 11 15
Pole,  , simple 11 14 15 97 101 123 139 213 322 342 , simple 11 14 15 97 101 123 139 213 322 342
Pole, 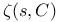 103 103
Pole, 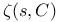 , multiplicity 103 , multiplicity 103
Pole, 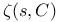 , simple 103 , simple 103
Pole, 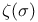 17 17
Pole, 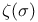 , residue 17 , residue 17
Pole, 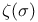 , simple 17 , simple 17
Pole, L-function 100
Pole, L-function, location 100
Pole, Li(s) 221
Pole, meromorphic function 19
Pole, meromorphic function, counting 19
Pole, residue 38
Pole, Z(t, C) 103
Pole, Z(t, C), multiplicity 103
Pole, Z(t, C), simple 103
Pole, zeta functions 103
Polya 37 40 105 115 127 130 135 311 356 358 374 431
Polya’s conjecture, Riemann hypothesis 429 431 432
Polya’s theorem 356 357
Polynomial  517 517
Polynomial 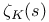 336 336
Polynomial Artin L-function 335
Polynomial Bernouilli 30
Polynomial characteristic 67 131
Polynomial Chebyshev 36
Polynomial cyclotomic 517
Polynomial degree 514
Polynomial introspective 516
Polynomial irreducible 514 517
Polynomial residue 517
Polynomial ring 512
Polynomial ring, Fermat’s little theorem 512
Polynomial ring, finite field 512
Polynomial time 509 511 512
Pomerance 512 521
Positive integer, introspective 516 517
Positive integer, perfect square 520
Poulsen 374
Power series 375
Power series, partial sum 375
Pratt 512
Premiers de la progression arithm?etique 241
Primality testing algorithms 63 319 509 511 513
Primality testing algorithms, Adleman — Huang 512
Primality testing algorithms, Adleman — Pomerance — Rumely 512
Primality testing algorithms, Atkin 512
Primality testing algorithms, conditional 512
Primality testing algorithms, elliptic curve 512
Primality testing algorithms, exponential time 512
Primality testing algorithms, exponential time, deterministic 512
Primality testing algorithms, extended Riemann hypothesis 509 512
Primality testing algorithms, Fermat’s little theorem 511
Primality testing algorithms, Fermat’s little theorem, polynomial ring 512
Primality testing algorithms, generalized Riemann hypothesis 63
Primality testing algorithms, Goldwasser — Kilian 512
Primality testing algorithms, Jacobi symbol 512
Primality testing algorithms, Miller 114 512
Primality testing algorithms, Miller — Rabin 63
Primality testing algorithms, Miller — Rabin, conditional deterministic 63
Primality testing algorithms, Miller — Rabin, conditional polynomial time 63
Primality testing algorithms, Miller — Rabin, generalized Riemann hypothesis 63
Primality testing algorithms, Miller, running time 114
Primality testing algorithms, polynomial time 509 511—513
Primality testing algorithms, polynomial time, deterministic 509 511 512
Primality testing algorithms, polynomial time, proof 509 513
Primality testing algorithms, polynomial time, randomized 512 513
Primality testing algorithms, Rabin 512
Primality testing algorithms, reciprocity law 512
Primality testing algorithms, running time 511 513
Primality testing algorithms, Solovay — Strassen 63
Primality testing algorithms, Solovay — Strassen, conditional deterministic 63
Primality testing algorithms, Solovay — Strassen, generalized Riemann hypothesis 63
Primality testing algorithms, Solovay’s primality test 512
Primality testing algorithms, Sophie Germain prime density 512 520
Primality testing algorithms, Sophie Germain prime density, time complexity 512 520
Primality testing algorithms, Strassen 512
Primality testing algorithms, unconditional 509 511 512
Primality testing problem 512
Prime see “Prime number”
Prime counting function 46 193 201 209 241 292 461
Prime decomposition 319
Prime k-tuple hypothesis 490
Prime k-tuple hypothesis, weak 490
Prime number 63 64 317 319 509 511
Prime number theorem 7 43 46 61 113 125 171 182 211 235 298 317 319—321 325 327 328 377 379 389 391 392 453 455 459 461 469 471 509
Prime number theorem, arithmetic progression 381 392
Prime number theorem, arithmetic progression, proof 381 392
Prime number theorem, auxiliary Tauberian theorem 463
Prime number theorem, conditional proof 171 182
Prime number theorem, consequence 447
Prime number theorem, Dirichlet series 325
Prime number theorem, equivalent statement 8 321 323 325 328 379 386 392 453 455 457 463 465 475 477 479
Prime number theorem, exposition 317
Prime number theorem, Gauss 46
Prime number theorem, history 317 319 459 462
Prime number theorem, Ikehara — Wiener Tauberian theorem 459 462
Prime number theorem, intuitive statement 8
Prime number theorem, large sieve 475 477
Prime number theorem, large sieve inequality 475
Prime number theorem, Liouville’s function 7
Prime number theorem, proof 18 125 211 235 299 320 325 327 377 379 389 391 401 453 455 471
Prime number theorem, proof, analytic 8 453 455
Prime number theorem, proof, Daboussi 469 475 477
Prime number theorem, proof, de la Vallee Poussin 8 9 47 61 125 235 317 322 323 455 461
Prime number theorem, proof, elementary 8 61 377 379 389 391 398 469 475
Prime number theorem, proof, Erdos 61 377 389 391 455 461 469 477 479
Prime number theorem, proof, Erdos — Selberg 389 399 400
Prime number theorem, proof, Hadamard 8 47 61 125 211 235 317 322 323 455 461
Prime number theorem, proof, Hardy — Littlewood 325 327
Prime number theorem, proof, Hildebrand 475 477
Prime number theorem, proof, Ikehara 455
Prime number theorem, proof, Korevaar 8 61 459 463
Prime number theorem, proof, Newman 61 453 455 457 459 462
Prime number theorem, proof, Selberg 61 377 379 386 387 389 392 396 455 461 469 477
Prime number theorem, proof, simplification 389 392 398 399
Prime number theorem, proof, Wiener 455
Prime number theorem, Riemann hypothesis 43
Prime number theorem, similar theorem 325 327
Prime number theorem, Wiener theory 462
Prime number, accumulation 201
Prime number, arithmetic progression 63 111 133 233 241 497
Prime number, arithmetic progression, distribution bound 115
Prime number, arithmetic progression, upper bound 497
Prime number, asymptotic behavior 225 231 233 235 239 240 274 317 319 461 489 520
Prime number, bad 394
Prime number, cardinality 319 320
Prime number, decomposition 319
Prime number, density 209 520
Prime number, density, sieve 512
Prime number, distribution 18 63 97—100 115 124 127 140 224 225 231 233 235 237 239 242 317 319 320 379 477 478 489 509
Prime number, distribution, sieve 477
Prime number, distribution, upper bound 477 478
Prime number, estimate 477
Prime number, good 394 398
Prime number, good, existence 394 396 399
Prime number, interval 63
Prime number, large 511
Prime number, location 63 379
Prime number, pair 41 130 319
Prime number, pair correlation 485 487 489
Prime number, pair, distribution 41 130
Prime number, power 500
Prime number, power, location 500
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



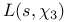
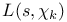
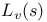
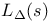
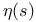






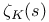


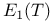
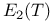
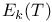
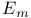
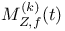


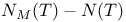
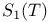

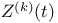

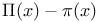
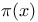
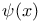
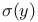
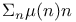


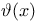
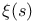
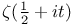
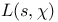
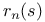
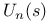
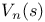



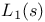
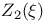
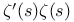 , residue
, residue