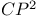|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Ботт Р., Ту Л.В. — Дифференциальные формы в алгебраической топологии |
|
|
 |
| Предметный указатель |
Уитни формула произведения для класса Понтрягина 296
Уитни формула произведения для класса Тодда 286
Уитни формула произведения для класса Эйлера 141
Уитни формула произведения для классов Чженя 278 281
Универсальная накрывающая 258
Универсальная накрывающая окружности 160
Универсальное подрасслоение 88 276
Универсальное подрасслоение над грассманианом 299
Универсальное подрасслоение над проективизацией расслоения 276
Универсальное подрасслоение над проективным пространством 274
Универсальное факторрасслоение и когомологии грассманиана 300
Универсальное факторрасслоение над грассманианом 299 305
Универсальное факторрасслоение над проективизацией расслоения 276
Универсальное факторрасслоение над проективным пространством 274
Универсальное факторрасслоение, классификация векторных расслоений 305
Универсальные классы Чженя 3
Универсальные коэффициенты, теорема 201
Унитарная группа 203 299
Унитарная группа, редукция структурной группы к ней 273
Унитарная группа, стабильные гомотопические группы 246
Унитарная группа, целочисленные когомологии 203
Упрощение расслоения 297
Усреднение 220 312
Физика 17
Фильтрация 164
Фильтрация индуцированная 167
Фильтрация на двойном комплексе 164
Фильтрация, длина 167
Фильтрованный комплекс 164
Фильтрованный комплекс спектральная последовательность 164
Флаг 288
Флагов многообразие 289
Флагов многообразие, кольцо когомологий 291
Флагов многообразие, полином Пуанкаре 292
Флагов многообразие, получение из грассманиана при помощи двух флаговых конструкций 300
Флаговое расслоение 289
Флаговое расслоение является расщепляющим многообразием 289
Флаговое расслоение, кольцо когомологии 292
Флаговое расслоение, ряд Пуанкаре 292
Формы с компактным носителем 16 33
Формы с компактным носителем, их интегрирование 38
Фундаментальная группа 29 213
Фундаментальная группа нерва хорошего покрытия 156
Фундаментальная группа римановой поверхности 9 246
Фундаментальная группа, тела симплициального комплекса совпадает с группой его путей 155
Функтор 28 118 «Ковариантный
Функториальность см. «Естественность»
Функции перехода векторного расслоения 64
Функции перехода двойственного расслоения 67
Функции перехода для прямой суммы 67
Функции перехода для расслоения 58
Функции перехода многообразия 28
Функции перехода расслоения плотностей 96
Функции перехода редукция структурной группы 65
Функции перехода сопряженного расслоения 293
Функции перехода тензорного произведения 67
Характеристические классы 16 272 «Классы «Классы
Хилтон, П. 271
Хирцебрух, Ф. 286
Хирцебруха формула для сигнатуры 297
Хирцебруха — Римана — Роха теорема 286
Хопф, Х. 16 234 272
Хопфа инвариант 234 240
Хопфа инвариант расслоения Хопфа 241
Хопфа инвариант, гомотопическая инвариантность 234
Хопфа инвариант, определение с помощью дифференциальных форм 236 336
Хопфа инвариант, определение с помощью теории пересечений 236
Хопфа инвариант, определение через степень 240
Хопфа инвариант, равенство нулю для расслоений f: 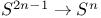 в случае нечетного n 234 в случае нечетного n 234
| Хопфа расслоение 233
Хопфа расслоение, слой над  244 244
Хопфа расслоение, слой над 0 244
Хопфа расслоение, Хопфа инвариант 241
Хопфа теорема об индексе 137
Хорошие покрытия 52
Хорошие покрытия на многообразии 52
Хорошие покрытия на топологическом пространстве 155
Хорошие покрытия на торе 114
Хорошие покрытия на триангулируемом пространстве 198
Хорошие покрытия являются кофинальными 53 198
Цепногомотопически обратное 113
Цепногомотопно 42
Цепное отображение 25
Цилиндр отображения 255
Чашечное произведение 199
Чеха граничный оператор 193
Чеха когомологии изоморфны когомологиям де Рама 108 113 121
Чеха когомологии одни и те же для всех хороших покрытий 109
Чеха когомологии окружности 110
Чеха когомологии открытого покрытия 107 109 119
Чеха когомологии пространства 121
Чеха когомологии со значениями в предпучке 121
Чеха коцепи со значениями в предпучке 119
Чеха — де Рама изоморфизм, доказательство с помощью диагональной леммы 147
Чеха — де Рама изоморфизм, доказательство с помощью спектральной последовательности 174
Чеха — де Рама изоморфизм, как изоморфизм градуированных алгебр 183
Чеха — де Рама изоморфизм, как применение принципа Майера — Вьеториса 108
Чеха — де Рама изоморфизм, явная формула 133
Чеха — де Рама комплекс 106
Чжень Шен-шень 17 272
Число зацепления 235
Штифель, Э. 272
Эйленберга — Маклейна пространство 18 246 256
Эйленберга — Маклейна пространство, 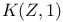 246 246
Эйленберга — Маклейна пространство, 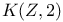 248 248
Эйленберга — Маклейна пространство, 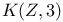 251 251
Эйленберга — Маклейна пространство, 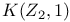 248 248
Эйленберга — Маклейна пространство,  249 249
Эйленберга — Маклейна пространство, кольцо рациональных гомотопий 151
Эйленберга — Стинрода аксиомы 13
Эйлера число 131
Эйлера число и локальная степень 133
Эйлера число равно индексу самопересечения диагонали 137
Эйлера число равно Эйлера характеристике 137
Эйлеров класс 83 125
Эйлеров класс двойствен по Пуанкаре к множеству нулей сечения 134
Эйлеров класс и спектральные последовательности 179
Эйлеров класс и старший класс Чженя 279
Эйлеров класс не зависит от выбора хорошего покрытия 128
Эйлеров класс ориентируемого 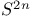 -расслоения 135 -расслоения 135
Эйлеров класс ориентируемого векторного расслоения 127
Эйлеров класс расслоения, нормального к 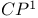 в в 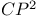 86 86
Эйлеров класс, 2-сферы 134
Эйлеров класс, выражение через функции перехода 84
Эйлеров класс, есть обратный образ класса Тома 141
Эйлеров класс, связь с последовательностью Гизина 187
Эйлеров класс, формула произведения 141
Эйлерова характеристика 135
Эйлерова характеристика равна эйлерову числу 137
Эйлерова характеристика расслоения 190
Эквивалентно ориентированные тривиализации 65
Эквивалентные коциклы 65
Элементарные симметрические функции 284
Эффективное действие 57
Ядро отображения множеств 216
Якоби матрица 71 230
Якобиан 36
Янг-Миллс 17
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



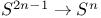 в случае нечетного n
в случае нечетного n 
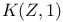
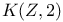
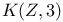
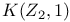

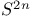 -расслоения
-расслоения 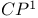 в
в