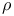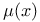|
|
 |
| Àâòîðèçàöèÿ |
|
|
 |
| Ïîèñê ïî óêàçàòåëÿì |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hartle J.B. — Gravity: An Introduction to Einstein's General Relativity |
|
|
 |
| Ïðåäìåòíûé óêàçàòåëü |
Naked singularity 319
National Radio Astronomy Observatory (NRAO) 225
Neutrinos 91
Neutron matter see “Ground state matter”
Neutron stars 7 244 250 255 515 527 533 see “Pulsars”
Neutron stars, accretion disks around 282
Neutron stars, endstates of stellar evolution 515 533
Neutron stars, mass vs. radius 528 (figure)
Neutron stars, maximum mass 256 528
Neutron stars, stability 533
Neutron stars, tour through 515
Newton's Law of Gravity see “Gravitational interaction”
Newton's laws of motion see “Newtonian mechanics” “Special
Newton's second law in curved spacetime 261 (box)
Newton's Theorem 40
Newtonian field equation see “Newtonian gravity”
Newtonian gravity 38—41
Newtonian gravity, compared to general relativity 452 (table) 486
Newtonian gravity, compared with electrostatics 39 (table)
Newtonian gravity, conflict with special relativity 107
Newtonian gravity, deviation equation 446
Newtonian gravity, deviation equation, compared with equation of geodesic deviation 452 (table)
Newtonian gravity, deviation equation, limit of equation of geodesic deviation 454
Newtonian gravity, field equation 40 486
Newtonian gravity, field equation, compared with Einstein equation 452 (table)
Newtonian gravity, field equation, related to tidal gravitational forces 450
Newtonian gravity, force between two masses 38
Newtonian gravity, geometric formulation 126—131
Newtonian gravity, gravitational constant G 38
Newtonian gravity, gravitational field 39
Newtonian gravity, gravitational field, created by acceleration 112
Newtonian gravity, gravitational field, eliminated by free-fall 112
Newtonian gravity, gravitational potential 38
Newtonian gravity, gravitational potential, compared to metric 452 (table)
Newtonian gravity, Kepler's law 40 253 504
Newtonian gravity, mass defined/measured by distant orbit 187
Newtonian gravity, mass density as source 39
Newtonian gravity, Newton's law of gravitv 107
Newtonian gravity, Newton's second law compared with geodesic equation 452 (table)
Newtonian gravity, Newton's theorem 40
Newtonian gravity, Newtonian and geometric, formulations compared 168 (table)
Newtonian gravity, tidal gravitational forces 445—450
Newtonian gravity, tidal gravitational forces, and tides 448 (box)
Newtonian gravity, tidal gravitational forces, compared to Riemann curvature 452 (table)
Newtonian gravity, tidal gravitational forces, defined 448
Newtonian gravity, tidal gravitational forces, outside a spherical mass 448
Newtonian mechanics, action summarizing 43
Newtonian mechanics, approximation to special relativity 77 87 88
Newtonian mechanics, flat space assumed 31
Newtonian mechanics, Newton's first law 15 31
Newtonian mechanics, Newton's second law 36
Newtonian mechanics, stability 528—533
Newtonian mechanics, stability, determined by squared frequent of modes 529
Newtonian mechanics, stability, illustrated by vibrating string 530
Newtonian mechanics, stable equilibrium 529
Newtonian mechanics, unstable equilibrium 529
Newtonian mechanics, variational principle 43
NGC (New General Catalog) 285n
NGC4258 see “Black holes in
Normal vector see “Three-surfaces”
Nuclear binding energy 256 (figure)
Nucleosynthesis see “Universe thermal
Null, cones see “Light cones”
Null, four-vectors 78
Null, separation 58
Null, surfaces see “Three-surfaces null”
Null, world lines 59 91
Null, world lines, tangent to light cone 59
Number, conservation of 472 473
Number, current 472
Number, current density 472
Number, density 471—473
Number, flux 472
Number, number-current four-vector 472
Obsener 95
Obsener, laboratory of 96
Obsener, observations referred to orthonormal basis 97
Obsener, orthonormal basis of 97—99 154
Obsener, orthonormal basis of accelerating 97
Obsener, particle energy measured by 98 154
Obsener, world line of 96
One-forms see “Dual vectors”
Orthonormal bases see “Bases orthonormal”
Parallel propagation, Parallel transport see “Vectors”
Parametrized post-Newtonian (PPN) framework 221—223
Parametrized post-Newtonian (PPN) framework, PPN parameter 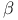 measurements 230—232 measurements 230—232
Parametrized post-Newtonian (PPN) framework, PPN parameter 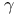 measurements 223—230 305 measurements 223—230 305
Parametrized post-Newtonian (PPN) framework, PPN parameters and deflection of light 223
Parametrized post-Newtonian (PPN) framework, PPN parameters and precession of the perihelion 223
Parametrized post-Newtonian (PPN) framework, PPN parameters and time delay of light 223
Paris — Lyon railway 55 (box)
Parsec 235n
Particles, energy 87
Particles, energy, measured by an observer 98 154
Particles, energy-momentum 87
Particles, rest mass 86
Particles, three-momentum 87
Particles, timelike world lines of 59
Past light cones see “Light cones”
Pauh exclusion principle see “Exclusion principle”
Penrose diagram, for flat space 137 (box)
Penrose diagram, for the Sehwarzschild geometry 274 (box)
Penrose process see “Kerr geometry”
Perfect fluids 479—480
Perfect fluids, defined 479
Perfect fluids, energy density 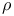 479 479
Perfect fluids, four-velocity u 479
Perfect fluids, pressure p 479
Perfect fluids, stress-energy, curved spacetime 480
Perfect fluids, stress-energy, flat spacetime 479
Perfect fluids, stress-energy, relation to pressure and energy density 479
Periastron 204 251
photons see also “Light rays”
Photons, energy and momentum 92
Photons, four-momentum 92
Photons, wave four-vector 92
Photons, wave three-vector 92
Photons, zero rest mass 92
Planck energy 11
Planck length 11
Planck time 11
PPN see “Parametrized post-Newtonian”
Precession of the equinoxes 231
Precession of the perihelion 231 see particle
Precession of the perihelion, and PPN parameters 223
Precession of the perihelion, confusion with solar quadrupole moment 231
Precession of the perihelion, Mercury's and periastron precession of binary pulsar PSR B1913+16 251
Precession of the perihelion, Mercury's measurement of 230—232
Pressure, example of stress 476
Pressure, Fermi 255 257
Pressure, geometrized units 479
Pressure, nonthermal 255 515
Principle of relativity 49
Principle of relativity, and connections between inertial frames 37
Principle of relativity, and equivalence of inertial frames 36
Principle of relativity, and the geometry of space 38
Principle of relativity, implemented by four-vectors 78
Principles of physics 36
Proper time see also “World lines proper
Proper time, distance along timelike world lines 60 82 142
Proper time, parameter along timelike world lines 82
PSRB1913+16 see “Binary pulsar PSR B1913+16”
Pulsars 251 534
Pulsars, as clocks 252
Pulsars, in binary pulsar 251
Quadrupole formula for energy loss by gravitational waves see “Gravitational waves”
Quadrupole moment, Newtonian gravitational potential of 231
Quadrupole moment, of the Sun 232
Quadrupole moment, tensor 506
Quantum cosmology 381 (box) 410
| Quantum gravity 11—12 381
Radio interferometry 225 226
Raising and lowering indices see “Indices”
Recombination see “Universe” “Thermal
Redshift see “Gravitational redshift” “Cosmological and
Redshift-(angular size) relation see “FRW cosmological models”
Redshift-magnitude relation see “FRW cosmological models”
Reference frame see “Frames”
Relativistic beaming 93—94 101
Relativistic gravity, when important 6—10
Relativistic stars 515—537 also
Relativistic stars, Einstein equation for 521
Relativistic stars, endstates of stellar evolution 7
Relativistic stars, equations of structure 520—523 535 537
Relativistic stars, equations of structure, how to solve 523
Relativistic stars, equations of structure, Newtonian limit 521
Relativistic stars, hydrostatic equilibrium see “Equations of structure”
Relativistic stars, maximum mass 535—537
Relativistic stars, stability 528—533
Relativistic stars, stability, changes at extrema of M vs. R 533
Relativistic stars, stability, changes at zero-frequency modes 532 532
Relativistic stars, stability, deduced from mass vs. radius relation 533
Relativistic stars, stability, of ground state matter models 533
Relativistic stars, stability, radial modes 531
Relativistic stars, stellar models, computation of 523—524
Relativistic stars, stellar models, for degenerate free fermions 524 525
Relativistic stars, stellar models, for ground state matter 528 (figure) 533
Relativistic stars, stellar models, for white dwarfs 524 525
Relativity of simultaneity see “Simultaneity”
Rest mass, defined 86
Rest mass, density 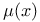 486 486
Rest mass, zero 92
Ricci curvature see “Curvature”
Ricci curvature scalar see “Curvature”
Ricci tensor see “Curvature”
Riemann curvature see “Curvature”
Riemann normal coordinates see “Coordinates”
Riemann tensor see “Curvature” “Riemann”
Ring interferometric gyros 35 (box)
Robertson — Walker metrics see “FRW cosmological models homogeneous isotropic
Rotating black holes see “Kerr geometry”
Rotation, metric outside a slowly rotating body 302 303
Rotation, metric outside a slowly rotating body, derived 497—498
Rulers, devices to measure spacelike distances 60
Sagnac effect 35 {box) 164
scalar 427
Scalar product see “Four-vectors”
Schwarzschild black holes see “Schwarzschild geometry”
Schwarzschild coordinates see “Schwarzschild geometry”
Schwarzschild geometry 186—215 256—276 also “Black
Schwarzschild geometry, as a black hole 256—262 273—275
Schwarzschild geometry, as a wormhole 273 (box)
Schwarzschild geometry, different coordinates compared 275
Schwarzschild geometry, Eddington — Finkelstein coordinates 256—262
Schwarzschild geometry, Eddington — Finkelstein coordinates, metric 258
Schwarzschild geometry, Eddington — Finkelstein coordinates, r = 2M not singular 258
Schwarzschild geometry, Eddington — Finkelstein coordinates, radial light rays 259 260
Schwarzschild geometry, event horizon see “Horizon”
Schwarzschild geometry, fate of observer who falls in 455
Schwarzschild geometry, freely falling frame in 441
Schwarzschild geometry, geodesic deviation in 455
Schwarzschild geometry, geodesies see “Particle orbits light
Schwarzschild geometry, gravitational redshift 189—191
Schwarzschild geometry, history 457n
Schwarzschild geometry, horizon, area 261
Schwarzschild geometry, horizon, as a null surface 261
Schwarzschild geometry, horizon, giometry 261—262
Schwarzschild geometry, horizon, one way property 261
Schwarzschild geometry, Killing vectors 186—187
Schwarzschild geometry, Kruskal diagram 270 271 272
Schwarzschild geometry, Kruskal extension 273 (box)
Schwarzschild geometry, Kruskal — Szekeres coordinates 269—275
Schwarzschild geometry, Kruskal — Szekeres coordinates, metric 269 270
Schwarzschild geometry, Kruskal — Szekeres coordinates, r = 2M not singular 258
Schwarzschild geometry, Kruskal — Szekeres coordinates, radial light rays 272
Schwarzschild geometry, Kruskal — Szekeres coordinates, related to Schwarzschild coordinates 271 (figure)
Schwarzschild geometry, light cones 259—261
Schwarzschild geometry, light ray orbits, deflection of light 210—212 235
Schwarzschild geometry, light ray orbits, effective potential 205
Schwarzschild geometry, light ray orbits, gallery of examples 207 (figure)
Schwarzschild geometry, light ray orbits, impact parameter b 206
Schwarzschild geometry, light ray orbits, time delay of light 212—215
Schwarzschild geometry, light ray orbits, which orbits escape 208 208
Schwarzschild geometry, mass 188
Schwarzschild geometry, mass, defined/measured by distant orbit 187
Schwarzschild geometry, metric in Schwarzschild coordinates 189
Schwarzschild geometry, Newtonian limit 187
Schwarzschild geometry, particle orbits, angular velocity of circular orbit 200
Schwarzschild geometry, particle orbits, bound 201—204
Schwarzschild geometry, particle orbits, conserved angular momentum 193
Schwarzschild geometry, particle orbits, conserved energy 193
Schwarzschild geometry, particle orbits, effective potential 194 196
Schwarzschild geometry, particle orbits, escape velocity 199
Schwarzschild geometry, particle orbits, gallery of examples 197 (figure)
Schwarzschild geometry, particle orbits, innermost stable circular (ISCO) 200
Schwarzschild geometry, particle orbits, lie in a plane 193
Schwarzschild geometry, particle orbits, Newtonian limit 194 195
Schwarzschild geometry, particle orbits, orbit defined 201
Schwarzschild geometry, particle orbits, precession 201—204 216
Schwarzschild geometry, particle orbits, radial plunge 197—200
Schwarzschild geometry, particle orbits, shape 201
Schwarzschild geometry, particle orbits, stable circular 200—201
Schwarzschild geometry, particle orbits, unstable circular 196
Schwarzschild geometry, Penrose diagram 274 (box)
Schwarzschild geometry, Riemann curvature 455
Schwarzschild geometry, Schwarzschild coordinates 186
Schwarzschild geometry, Schwarzschild coordinates, definition of radial coordinate 187
Schwarzschild geometry, Schwarzschild coordinates, metric 186
Schwarzschild geometry, Schwarzschild coordinates, r = 2M a coordinate singularity 257 270 455
Schwarzschild geometry, Schwarzschild radius r = 2M 188 235
Schwarzschild geometry, singularity at r = 0, 258 455
Schwarzschild geometry, singularity at r = 0, as a spacelike surface 262
Schwarzschild geometry, solves vacuum Einstein equation 186
Schwarzschild geometry, solving the Einstein equation to find 457
Schwarzschild geometry, symmetries of 186—187
Schwarzschild geometry, trapped surfaces 266 (box)
Schwarzschild geometry, unique spherically symmetric solution ot the vacuum Einstein equation (Birkoff's theorem) 257 310 (problem)
Schwarzschild metric see “Schwarzschild geometry”
Schwarzschild radius see “Schwarzschild geometry”
Schwarzschild, K. 186 457n
Second mass moment tensor 499
Separation, null, spacelike and timelike 58 142
Shapiro time delay see “Time delay ot light”
Shapiro, Irwin 212
Simultaneity, and light cones 59
Simultaneity, and Lorentz boosts 68
Simultaneity, in GPS 69
Simultaneity, in special relativity 51—52 68
Simultaneity, Newtonian physics 50
Simultaneity, relativity of 68—69
Simultaneity, rocket thought experiment 50 (figure)
Singularity theorems 266 (box) 275 381(box)
Singularity theorems, for FRW cosmological models 399 (problem)
Slowly-rotating body see “Rotation”
Space, spacelike surface the general notion of 160
Spacelike surface see “Three-surfaces spacelike”
Spacelike, distances, measured by rulers 60
Spacelike, four-vector 78
Spacelike, separation 58
Spacetime 52
Spacetime diagrams 52 55
Spacetime diagrams, as maps of spacetime 56
Spacetime diagrams, events as points in 53
Spacetime diagrams, railway train example 55 (box)
Spacetime of special relativity see “Flat spacetime”
Spacetime, dimensions, extra detectabled 157 (box)
Spacetime, dimensions, three spate and one time dimension assumed 140
Spacetime, events as points in 53
Spacetime, flat see “Flat spacetime”
Spacetime, point in 53
|
|
 |
| Ðåêëàìà |
 |
|
|
 |
 |
|
 |
|
Î ïðîåêòå
|
|
Î ïðîåêòå



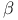 measurements
measurements 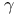 measurements
measurements