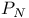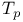Авторизация
Поиск по указателям
Kammler D.W. — First Course in Fourier Analysis
Обсудите книгу на научном форуме Нашли опечатку?
Название: First Course in Fourier AnalysisАвтор: Kammler D.W. Аннотация: This unique book provides a meaningful resource for applied mathematics through Fourier analysis. It develops a unified theory of discrete and continuous (univariate) Fourier analysis, the fast Fourier transform, and a powerful elementary theory of generalized functions and shows how these mathematical ideas can be used to study sampling theory, PDE's, probability, diffraction, musical tones, and wavelets. Providing unified development of (univariate) Fourier analysis for functions on R, T, Z, and P, the book also includes an unusually complete presentation of the Fourier transform calculus. It uses concepts from calculus to present an elementary theory of generalized functions. It also uses the FT calculus and generalized functions to study the (univariate) wave equation, diffusion equation, and diffraction equation. In addition, fine points of the theory are developed. The book also demonstrates real-world applications of Fourier analysis in the chapter on musical tones. A valuable reference on Fourier analysis for a variety of scientific professionals, including Mathematicians, Physicists, Chemists, Geologists, Electrical Engineers, Mechanical Engineers, and others.
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Издание: Second EditionГод издания: 2007Количество страниц: 798Добавлена в каталог: 13.04.2008Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Law of Large Numbers 778 Least squares approximation, and Fourier synthesis 75—76 84 Least squares approximation, and sampling theory 492 497 522 Legendre function 237 Leibnitz notation 372 Leibnitz rule for differentiation 107 375 398 455 457 459 Liberal arts 698 Lighthill, M.J. 451—452 Likelihood function 794 Lolipop plots 6 Lorenzian 22 LTI system 16 72 282 470 522 738 Maclaurin series 1 522 738 Maclaurin series, and weak convergence 438 Maclaurin series, for bandlimited function 486 517 Mallat's herringbone algorithm 606—607 645—646 see Mars orbit 13 70 Mason flow diagram for FFT 355 Max bound, for generalized function 784 Max bound, for probability density 745 783 Max flat trigonometric polynomial 633 Maxwell density 737 791 Mean 756 759 Mean 766—767 Mersenne's formula for frequency 536 Mesa function 373 454 754 see Michelson and Stratton harmonic analyzer 87 Midpoint regularization 45 Mirror, for boundary condition 569 Mirror, for Fourier Transform rules 134 Mirror, for reverse carry algorithm 305 Mnemonic 137 177 200 Modulation rule 137 177 199 260 413 Modulation, frequency 711 Modulation, index 711 715 Modulus of coninuity 598 643 Moments, for probability density and smoothness 757 785 Moments, for sum of random variables 766 Moments, for wavelet 618 621 680—681 Monochord 698 729 Monotonicity relation 744 Monticello 107 Mother wavelet 594 Movies, computing frames with FFT 571 Movies, for diffracting laser beam 572 590 Movies, for heat flow 572 Movies, for vibrating string 572 575 577 579—581 Movies, for water waves 591 Multiplication of generalized functions 398 Multiplication rule 144 170 177 199 413 Multiplication using FFT 113 Multiresolution analysis 597 642 684 Music, as mathematics 698 Music, beat 700 Music, for wavelets 597 600 674 Music, interval 694 697—699 Music, loudness 696 701 Music, pictogram 700 Music, pitch 694 700 702 A37 Music, samples 693 707—708 715 732 Music, scales 697—700 Music, score 693 701—703 Music, spectrogram 703 724 Music, timbre 707 Music, transformation 725 735 Musical tone 694 Musical tone, for bell 709 716 Musical tone, for brass 710 Musical tone, for string 710 731 Musical tone, from monochord 729 Musical tone, from noise 718—723 Musical tone, information content 728 Musical tone, local frequency 705—706 Musical tone, loudness 695 728 Musical tone, via additive synthesis 73 707—711 Musical tone, via computer 694 700 715 718 Musical tone, via FM synthesis 711—717 734 Newton's "method" 1 Newton's iteration 114 636 Nobel prize 22 A2 Noise, filtered 721 Noise, sound of 720 723 Noise, white 718 Normal density 139 150 739 772 775 794 795 Normal density, distribution function 740 A33 Normal vibration modes 536 702 Nyquist condition 486 705 717 Odd, function 62 64 247 Odd, generalized function 397 455 Odd, projection 245 Ohm's law of acoustics 696 729 Operation 292 Operation count, for additive, FM synthesis of tone 732 Operation count, for bit reversal permutation 354 Operation count, for FFT 299 323 327 358 Operation count, for FHT 325 Operation count, for FWT 608 646 692 Operation count, for naive DFT 292 294 Operators 16 239 A19—A22 Operators, blanket hypotheses 241—242 Operators, factorization of 257 Operators, for filter bank 656—660 Operators, for Mallat's herringbone 645 Operators, for pre-, post-processing 652 Operators, Fourier transform of 255—256 A19—A22 Operators, from complex conjugation 251—253 Operators, from powers of 243 Operators, Hartley transform of 263 Operators, LTI 16 72 282 470 Operators, projection 245 253—254 277 Operators, symmetry preserving 254 282 Orbit, for cardiod, rose, ... 225 Orbit, for Mars 13 70 Orbit, for Pallas 14 70 Orbit, for vibrating string 579 Orbit, symmetry of 225 Order of approximation 620 642—644 Orthogonal projection 642 Orthogonality relations, for complex exponentials 24—25 Orthogonality relations, for Hermite functions 166 Orthogonality relations, for sin, cos 75 Orthogonality relations, for sine functions 160 Orthogonality relations, for wavelets 602 625 642 Orthogonality relations, via centroid 74 Paley — Wiener theorem 517 Pallas 14 70 361 Papoulis sampling theorem 503—504 519 Parallel operation for FFT 343 Parseval identities 23—24 73—74 Parseval identities, for evaluating integrals 83 149 Parseval identities, for evaluating sums 190 221 226 Parseval identities, for generalized functions 391 466 Parseval identities, link to convolution 170 Parseval identities, validity 24 82 see Partial derivative of generalized function 438 Partial fractions 143 416 Partition of unity 171 446 622 PDE xiii 523 587 Periodic function 4 8 33 440 Periodic function, for ear 697 Periodization 32 535 550 569 671 Phase deaf 697 729 Pi, computation of 113—114 Piano, equitempered scale 699 Piano, for harmonic synthesis 73 Piano, keyboard frequencies A37 Piecewise, constant 81 Piecewise, continuous 26 76—77 81 121—123 126—128 Piecewise, polynomial 117 145 170 380 382—383 463 623 Piecewise, smooth 39 42 45 55 57 83—85 123 406 491 505 623 Pitch perception 694 Plancherel identities 24 Plancherel identities, for evaluating integrals 148 Plancherel identities, for evaluating sums 190 221 224 226 491 Plancherel identities, validity 30 76 82—83 Plancherel identities, via autocorrelation 162 Poisson probability density 781—782 Poisson process 782 Poisson relations 33—36 Poisson relations, for evaluating sums 149 Poisson relations, for finding Fourier series 179 262 478 488 Poisson relations, for unifying Fourier analysis 36—37 Poisson sum formula 39 50 393 488 Polarization identity 24 74 Polygon function 191 Power functions 329 395 401 456 Power functions, truncated 382 Power scaling rule 142 413 Primitive root 238 Probability density function 122 154 739 see Probability density function, Benford 798 Probability density function, Bernoulli 767 769 776 779 Probability density function, binomial 239 Probability density function, bivariate 764 Probability density function, Cauchy 758 760 775 Probability density function, chi squared 791 Probability density function, closure 787 Probability density function, coin flip 740 742 777 Probability density function, convolution of 765 Probability density function, die-toss 739 742 754 756 773 Probability density function, Dirac 757 775 Probability density function, for sum of random numbers 765—766 768 Probability density function, from characteristic function 741 Probability density function, from distribution function 740 Probability density function, gamma 781 Probability density function, Laplace 739 781 Probability density function, Maxwell 737 791 Probability density function, Poisson 739 781 Probability density function, standard normal 139 150 739—740 754 758 768 Probability density function, truncated exponential 742 757 771 777 Probability density function, uniform 739 742 Products, of generalized functions 398 Products, of probability functions 750 Projection operators 245 253—254 277—278 281 642 Ptolemy, C. 12 699 Pulse amplitude 511 Pythagoras and music 698 729—730 Quadratic residue 237 Quantization of samples 484 Quantum mechanics, Schroedinger equation 558 Quantum mechanics, uncertainty relation 762 Quantum mechanics, wave packet for free particle 563 Ramp function 227 381 Random number generator 194 718 Random variables 753 Random variables, characteristic function for 759 767 Random variables, generation of 194 718 795 Random variables, independent 764 Random variables, joint density 764 Random variables, max, min of 790 Random variables, sum of independent 764 Random variables, via probability density 253 Random walk 777 Rational function 143 159 416—419 465 Real world sampling theorem 507 Reciprocity relations 69 Recursion see “Recursion” Recursive algorthm for FFT 350—351 Reduced wave function 556 Reflection of light at mirror 569 Reflection operator 240 243 Reflection operator, tag 251 Reflection rule 135 177 199 413 Regular tails 48 53 55 82 85 Relatively prime 206 236 Repeat rule 202 232 257 261 Response of LTI system 282 419 470 471 Riemann sum 39 44 Riemann sum, and Gibbs phenomenon 44 Riemann sum, for Fourier coefficient 79 Riemann sum, for Fourier transform 79 Riemann — Lebesgue lemma 81 458 Risset's glissando 725 Rodrigues formula 151 Rules, for derivatives of generalized functions 405 Rules, for Fourier transforms of functions on 199—212 A17—A18 Rules, for Fourier transforms of functions on 132—147 A14 Rules, for Fourier transforms of functions on 176—182 187—190 A15—A16 Rules, for Fourier transforms of generalized functions 413 Rules, for manipulation of generalized functions 389 Same sign shift 137 see Sample-sum rule 210 212 284 Samples for Daubechies wavelet 652 687 689 Sampling 32 483 Sampling function see “Comb function” Sampling rule 210 214 262 Sampling theorem, for almost bandlimited functions 505 Sampling theorem, for generalized functions 487 Sampling theorem, for real-world signals 507 Sampling theorem, using fragments of 495 Sampling theorem, using niters 498 501 503 Sampling theorem, when F is piecewise smooth 491 497 Sampling, for wavelet analysis 649 668 685 Sampling, rate for audio 484 Scale for music 697—700 729 Scale for wavelet approximation 595—596 Scaling function for wavelets 597 609 Schoenberg, I. 19 72 125 Schroedinger's equation xiii 558 Schwartz functions 372—374 482 Schwartz functions, closure of 375 Schwartz, L. xii 368 451 Semitone 699 Shah function see “Comb function” Shannon's sampling theorem 491 Shannon, C. xiii 484 491 Shift rule see “Translation rule” Shuffle permutation 312 332 Shuffle permutation, action 315 332 341—342 Shuffle permutation, operator identities 314 333 342 364 Shuffle permutation, products for FFT 314 365 Signum function 228 380 424 Signum function, for Hilbert transform 267 Sin operator 63 67 246—247 Sin transform 63 67 247 287 Sinc function 130 Sinc function, properties 141 160 493 514—515 Singularity function, on 51—52 55 82—83 Singularity function, on 41—42 46 Slowly growing function 376 Slowly growing sequence 444 Smoothness of B-spline 117 193 Smoothness of convolution product 107 123 126 128 401 Smoothness of Fourier transform 48 81 153 169. Smoothness of solution of diffusion equation 542 Smoothness of solution of dilation equation 616—619 Soil temperature 547 586 Sparce matrix factorization 311 675 Spectral, density 719—720 Spectral, enrichment 715 731 Spectral, factorization 634 682 Spectrogram, for bell tone 616 709 Spectrogram, for Risset's glissando 726 Spectrogram, for shaped noise 721 723 Spectrogram, for Twinkle, Twinkle 703 Spectrogram, generation of 702—704 Spectroscopy 21 Spectrum of arginine 22 Standard deviation 756 Standard normal probability distribution A33
Реклама
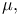for sum of random variables 
|
|
О проекте