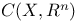|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Munkres J.R. — Topology: A First Course |
|
|
 |
| Предметный указатель |
"If ... then" 7
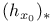 329 see 329 see
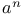 , definition 35 55 , definition 35 55
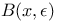 117 117
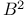 133 see 133 see
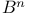 155 155
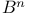 , compactness 175 , compactness 175
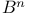 , path connectedness 155 , path connectedness 155
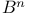 , simple connectedness 327 , simple connectedness 327
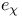 (constant path) 322 (constant path) 322
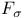 set 250 set 250
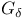 set 194 248 set 194 248
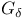 set and strong Urysohn lemma 215 set and strong Urysohn lemma 215
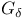 set is Baire 296 set is Baire 296
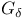 set is topologically complete 270 set is topologically complete 270
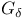 set, set, 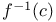 is a 215 238 is a 215 238
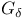 set, closed set is a 248 250 set, closed set is a 248 250
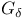 set, irrationals 250 set, irrationals 250
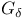 set, points of continuity form a 296 297 set, points of continuity form a 296 297
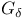 set, rationals 295 set, rationals 295
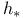 , dependence on base point 330 , dependence on base point 330
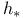 , dependence on homotopy class of h 369 , dependence on homotopy class of h 369
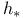 , functorial properties 329 , functorial properties 329
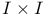 in dictionary order, closures in 101 in dictionary order, closures in 101
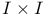 in dictionary order, connectedness 156 in dictionary order, connectedness 156
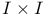 in dictionary order, linear continuum 154 in dictionary order, linear continuum 154
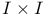 in dictionary order, local connectedness 163 in dictionary order, local connectedness 163
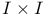 in dictionary order, metrizability 195 in dictionary order, metrizability 195
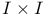 in dictionary order, path connectedness 156 in dictionary order, path connectedness 156
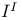 , countable dense subset 195 , countable dense subset 195
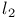 126 126
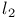 , completeness 270 , completeness 270
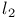 , countable dense subset 195 , countable dense subset 195
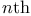 root function, continuity 111 root function, continuity 111
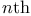 root function, existence 158 root function, existence 158
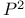 352 352
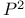 , fundamental group 353 , fundamental group 353
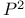 , surface 352 , surface 352
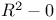 321 321
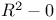 , covering by , covering by 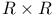 334 334
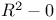 , fundamental group 343 , fundamental group 343
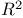 , standard topology 87 , standard topology 87
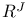 in box topology is Baire 297 in box topology is Baire 297
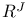 in box topology is topological group 144 in box topology is topological group 144
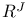 in product topology is Baire 297 in product topology is Baire 297
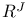 in product topology is topological group 144 in product topology is topological group 144
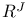 in product topologyá metrizability 131 in product topologyá metrizability 131
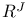 in product topologyá normality 205 in product topologyá normality 205
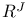 in uniform topology 122 in uniform topology 122
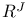 in uniform topology is Baire 297 in uniform topology is Baire 297
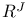 in uniform topology is topological group 144 in uniform topology is topological group 144
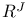 in uniform topologyá completeness 266 in uniform topologyá completeness 266
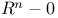 155 155
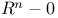 , fundamental group 344 , fundamental group 344
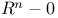 , path connectedness 155 350 , path connectedness 155 350
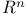 37 37
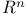 , basis for 115 , basis for 115
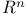 , compact sets in 174 , compact sets in 174
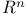 , completeness 264 , completeness 264
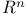 , local compactness 183 , local compactness 183
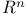 , local path connectedness 161 , local path connectedness 161
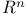 , metrics for 121 , metrics for 121
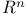 , second-countability 190 , second-countability 190
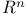 , simple connectedness 326 , simple connectedness 326
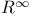 116 125 274 116 125 274
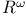 37 37
 in box topology see also “ in box topology see also “ in box topology” in box topology”
 in box topology, complete regularity 237 in box topology, complete regularity 237
 in box topology, components 163 in box topology, components 163
 in box topology, connectedness 152 in box topology, connectedness 152
 in box topology, metrizability 130 in box topology, metrizability 130
 in box topology, normality 206 in box topology, normality 206
 in box topology, paracompactness 206 in box topology, paracompactness 206
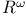 in product topology see also “ in product topology see also “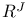 in product topology” in product topology”
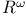 in product topology, completeness 265 in product topology, completeness 265
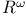 in product topology, local compactness 183 in product topology, local compactness 183
 in product topology, local path connectedness 161 in product topology, local path connectedness 161
 in product topology, metrizability 123 in product topology, metrizability 123
 in product topology, second-countability 190 in product topology, second-countability 190
 in uniform topology see also “ in uniform topology see also “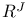 in uniform topology” in uniform topology”
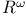 in uniform topology, components 163 in uniform topology, components 163
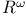 in uniform topology, second-countability 191 in uniform topology, second-countability 191
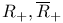 31 31
 82 82
 vs. standard topology on R 82 vs. standard topology on R 82
 , countability axioms 192 , countability axioms 192
 , metrizability 195 , metrizability 195
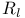 , normality 202 , normality 202
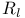 , paracompactness 256 259 , paracompactness 256 259
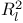 193 193
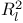 , complete regularity 237 , complete regularity 237
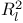 , Lindelof condition 193 , Lindelof condition 193
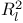 , normality 202 , normality 202
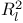 , paracompactness 256 , paracompactness 256
 106 106
 , covering by R 332 , covering by R 332
 , covering spaces classified 393 , covering spaces classified 393
 , coverings by , coverings by  335 336 335 336
 , fundamental group 340 , fundamental group 340
 138 138
 , simple connectedness 347 351 , simple connectedness 347 351
 , vector fields on 367 , vector fields on 367
 156 156
 , compactness 175 , compactness 175
 , fixed-point theorem for 374 , fixed-point theorem for 374
 , path connectedness 156 , path connectedness 156
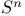 , simple connectedness 350 , simple connectedness 350
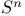 , vector fields on 369 374 , vector fields on 369 374
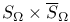 , complete regularity 236 , complete regularity 236
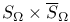 , normality 201 , normality 201
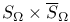 , paracompactness 256 , paracompactness 256
 66 66
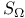 , compactness properties 178 , compactness properties 178
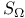 , countability axioms 194 , countability axioms 194
 , metrizability 179 , metrizability 179
 , paracompactness 259 261 , paracompactness 259 261
 , Stone — Cech compactification 243 , Stone — Cech compactification 243
 , uniqueness 73 , uniqueness 73
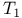 axiom 99 axiom 99
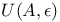 177 177
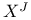 38 38
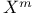 36 36
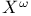 37 37
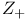 32 32
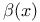 see “Stone — Cech compactification” see “Stone — Cech compactification”
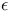 -ball 117 -ball 117
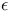 -neighborhood of a set 177 -neighborhood of a set 177
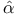 327 327
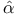 is isomorphism 327 is isomorphism 327
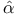 , independence of path 330 , independence of path 330
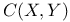 267 see “Compact-open “Uniform 267 see “Compact-open “Uniform
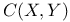 , closedness in , closedness in 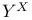 267 281 283 267 281 283
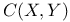 , compact subsets of 290 , compact subsets of 290
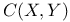 , completeness 267 , completeness 267
 11 11
 77 77
 , , 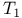 axiom 100 axiom 100
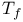 , compactness 167 , compactness 167
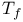 , connectedness 151 , connectedness 151
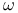 -tuple 37 -tuple 37
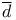 119 119
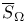 66 66
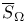 , metrizability 131 , metrizability 131
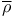 122 266 see 122 266 see
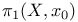 326 see 326 see
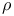 120 267 see 120 267 see
 -locally discrete 254 -locally discrete 254
 -locally finite 247 -locally finite 247
2-complex 306
2-complex, imbedding in 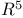 310 310
| 2-complex, topological dimension 306
2-sphere 138 see
Abelian fundamental group 330 354 355
Absolute neighborhood retract 221
Absolute retract vs. universal extension properly 221
Accumulation point of a net 188
Action of a group on a space 356
Addition operation 30
Adjunction space 221
Alexander horned sphere 385
Algebraic numbers 51
ANR 221
Antipodal map 353
Antipodal point 352
Antipode-preserving map 361
ar 221
ARC 375
Archimedean ordering 33
Arzela’s theorem 279 292
Ascoli’s theorem, classical version 277
Ascoli’s theorem, general version 290
Axiom of Choice 59
Axiom of choice, equivalent statements 62 74
Axiom of choice, finite 61
Baire category theorem 294
Baire category theorem, special case 177 203
Baire space 293
Baire space, 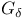 set 296 set 296
Baire space, 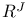 297 297
Baire space, compact Hausdorff space 294
Baire space, complete metric space 294
Baire space, fine topology on 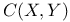 297 297
Baire space, irrationals 296
Baire space, locally compact Hausdorff space 296
Baire space, open subset 296
Ball, unit see “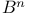 ” ”
Barber of Seville paradox 48
Base point 326
Base-point choice, effect on 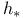 330 330
Base-point choice, effect on 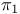 328 328
Basis for a topology 78 81
Bd A 101
Bijective function 19
Binary operation 30
Bing metrization theorem 254
Bolzano — Weierstrass property 178
Borsuk theorem 377
Borsuk — Ulam theorem for 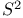 361 361
Boundary 101
Bounded above 27
Bounded below 27
Bounded metric, standard 119
Bounded set 119
Box topology 113
Box topology vs. product topology 114
Box topology, basis for 114
Box topology, compactness properties 181
Box topology, Hausdorff condition 115
Box topology, subspace 114
Brouwer fixed-point theorem for 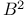 365 365
Brouwer fixed-point theorem for 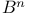 369 369
Brouwer invariance of domain 378 387
Cantor set 177
Cardinality, comparability for two sets 68
Cardinality, greater 62
Cardinality, same 52
Cartesian product of two sets 13
Cartesian product, general 36—38
Cauchy sequence 264
Choice axiom see “Axiom of choice”
Choice function 59
Circle, unit see “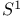 ” ”
Cl A 95
Classification of covering spaces 388 392 393
Closed graph 172
Closed interval 84
Closed map 135 172
Closed ray 86
Closed refinement 251
Closed set 92
Closed set in subspace 94
Closure 94
Closure in a subspace 95
Closure of a cartesian product 100 116
Closure of a connected set 149
Closure of a union 100 246
Closure via basis elements 95
Closure via limit points 97
Closure via nets 188
Closure via sequences 128 190
Cluster point 96
Coarser topology 77
Cofinal 187
Coherent topology 216
Collection 11
Comb space 156
Compact convergence topology 282 see
Compact convergence topology vs. compact-open topology 286
Compact convergence topology vs. pointwise convergence topology 283 290
Compact convergence topology vs. uniform topology 283
Compact convergence topology, convergent sequences in 282
Compact convergence topology, first-countability 283
Compact convergence topology, independence of metric 287
Compact convergence topology, regularity 283
Compact Hausdorff space is Baire 294
Compact Hausdorff space, 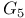 set is Baire 296 set is Baire 296
Compact Hausdorff space, components 235
Compact Hausdorff space, imbedding in 237
Compact Hausdorff space, metrizability 220
Compact Hausdorff space, normality 198
Compact Hausdorff space, paracompactness 255
Compact Hausdorff space, quasicomponents 235
Compact space 164 see
Compact support 284
Compact-open topology 286 290
Compact-open topology vs. compact convergence topology 286
Compact-open topology, continuity of evaluation map 287
Compact-open topology, Hausdorff condition 289
Compact-open topology, regularity 289
Compactification 238 see
Compactification of (0, 1) 239
Compactification, induced by an imbedding 239
Compactification, one-point 183
Compactly generated space 282
Compactness 164 see
Compactness in 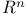 174 174
Compactness in 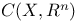 277 279 277 279
Compactness in 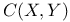 290 290
Compactness in 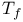 167 167
Compactness in Hausdorff metric 279
Compactness in order topology 173 177
Compactness in R 174
Compactness in uniform topology 181
Compactness of box topology 181
Compactness of closed intervals 174
Compactness of continuous image 167
Compactness of countable products 278
Compactness of finite products 167
Compactness of products 232
Compactness of subspace 165
Compactness via nets 188
Compactness via sequences 181
Compactness vs. completeness 275
Compactness vs. limit point compactness 178 181 194
Compactness vs. second-countability 194
Compactness, closed set criterion for 170
Comparability of cardinalities 68
Comparability of well-ordered sets 73
Complement 10
Complete graph on five vertices 304 386
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 , definition
, definition 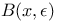
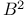
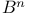
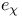 (constant path)
(constant path) 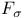 set
set 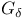 set
set 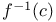 is a
is a 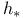 , dependence on base point
, dependence on base point  in dictionary order, closures in
in dictionary order, closures in  , countable dense subset
, countable dense subset 
 root function, continuity
root function, continuity 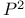
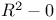
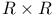
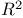 , standard topology
, standard topology 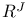 in box topology is Baire
in box topology is Baire 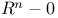
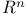
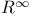
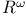
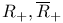
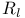
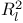
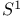
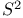
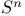
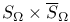 , complete regularity
, complete regularity 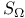
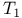 axiom
axiom 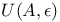
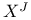
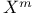
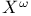
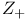
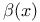
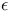 -ball
-ball 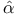
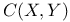
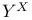
 -tuple
-tuple 
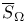
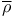
 -locally discrete
-locally discrete 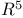
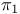
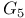 set is Baire
set is Baire