|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Леман Э. — Теория точечного оценивания |
|
|
 |
| Предметный указатель |
Непараметрическая задача одной выборки 98 234 238 281
Непараметрическое семейство 14 31 44 68 97 101 128
Непрерывная достаточная статистика 48
Неравенство Бхаттачария 122 134
Неравенство информации 110 116 134
Неравенство Йенсена 53 56 69 363 364
Неравенство Кифера 133
Неравенство ковариации 115 117 118 123
Неравенство Крамера — Рао 134
Неравенство Хаммерсли — Чемпена — Роббинса 111
Неравенство Чебышева 295 345
Неравенство Шварца 69 123
Несмещенная с локально минимальной дисперсией оценка (НЛМД-оценка) 77 110 123 131
Несмещенная с локально минимальной дисперсией оценка, случай, когда не существует 81 123
Несмещенная с локально минимальной дисперсией оценка, характерйзация 144 145
Несмещенная с локально минимальной дисперсией оценка, эквивариантная относительно сдвига 143 см. «Эквивариантная
Несмещенная с равномерно минимальной дисперсией оценка (НРМД-оценка) 75 77 134
Несмещенная с равномерно минимальной дисперсией оценка (НРМД-оценка) в выборе из конечной совокупности 193 195
Несмещенная с равномерно минимальной дисперсией оценка (НРМД-оценка) в линейной модели 170 179
Несмещенная с равномерно минимальной дисперсией оценка (НРМД-оценка) в модели со случайными эффектами 181 183
Несмещенная с равномерно минимальной дисперсией оценка (НРМД-оценка) в ограниченной полиномиальной модели 185
Несмещенная с равномерно минимальной дисперсией оценка (НРМД-оценка) в сравнении с ОМП 108 109
Несмещенная с равномерно минимальной дисперсией оценка (НРМД-оценка) в сравнении с ЭМР-оценкой 150
Несмещенная с равномерно минимальной дисперсией оценка (НРМД-оценка) в таблицах сопряженности признаков 186
Несмещенная с равномерно минимальной дисперсией оценка (НРМД-оценка) вектора параметров 262
Несмещенная с равномерно минимальной дисперсией оценка (НРМД-оценка), пример одной неразумной оценки 109
Несмещенное квадратичное оценивание с минимальной нормой 184
Несмещенное оценивание ковариации 88 102 125 128
Несмещенность 13 75 76 134 151
Несмещенность для вектора параметров 262 см. «Несмещенная «Несмещенная «Несмещенность
Несмещенность и байесовское оценивание 223
Несмещенность по риску 152 201 203 210
Несмещенность по риску, отношение к эквивариантности 158 165 см. «Медианная
Несмещенность по среднему 13 151 см.
Несобственное априорное распределение 221 222 225 232 284 407 425
Несобственное априорное распределение и эквивариантные оценки 253
Нижний предел 20 62 347
Новик 217 290
Нордберг 398 430
Норден 387 430
Нормальная авторегрессионная марковская последовательность 398
Нормальная весовая функция 343
Нормальная смесь 133 391 см. «Модель
Нормальное распределение как априорное распределение 222
Нормальное распределение как наименее информативное 147
Нормальное распределение как экспоненциальное семейство 35 38
Нормальное распределение Нормальное распределение 28 38 40 43 49
Нормальное распределение, достаточные статистики 43 44 46
Нормальное распределение, информация Фишера 114 120 121
Нормальное распределение, производящая функция моментов и моменты 39 см. «Многомерное «Урезанное
Нормальное среднее, байесовская оценка 222
Нормальное среднее, допустимая минимаксная оценка 273
Нормальное среднее, допустимая оценка 239 240
Нормальное среднее, минимаксная оценка 233 281
Нормальное среднее, ограниченная байесовская оценка 237
Нормальное среднее, оценка вектора средних многомерного нормального распреде¬ления 262 264 267 277
Нормальное среднее, усеченная задача оценивания 242
Нормальное среднее, целочисленная оценка 132
Нормальное среднее, эквивариантная с минимальным риском оценка 146 166 см. «Сжимающая «Среднее
Нормирующие постоянные 298 300 307 346 348 397 399
Носитель распределения 26 63 67
НРМД-оценка см. «Несмещенная с разномерной минимальной дисперсией оценка»
Нуль-множество 24 68
Ньюкомб 316 354
Нэт 138
Обратный биномиальный выбор 90 см.
Общая дисперсия 399
Общее среднее в оценивании 87 125
Общее среднее в оценивании в эффективном оценивании
Общее среднее в оценивании, несуществование НРМД-оценки 124
Ограниченная байесовская оценка 237 278
Ограниченная функция потерь 58 69 81 146
Ограниченность по вероятности 347
Одновременное оценивание 251 260
Одновременное оценивание в экспоненциальных семействах 278
Одновременное оценивание вектора средних многомерного нормального распределения 262
Однофакторная модель 168 173 174 203 225 268
Окрестность распределения 15 83 335
Олкин 88 136 138 263 291
Ортогональное преобразование 262 264
Остерхоф 303 354
Острайт 327 355
Отношение дисперсий, оценивание 87
Отрицательное биномиальное распределение 33 64 90 126 131 282
Оценка 12 25
Оценка Джеймса — Стейна 265 299 308
Оценка Джеймса — Стейна максимально возможный риск компонент 286
Оценка Джеймса — Стейна функция риска 269
Оценка Джеймса — Стейна, недопустимость 272 273 275
Оценка максимального правдоподобия (ОМП) 108 184 186 335 364 387 426
Оценка максимального правдоподобия (ОМП) ограниченная 184
Оценка максимального правдоподобия (ОМП), асимптотическая эффективность 370 426
Оценка максимального правдоподобия (ОМП), локально асимптотическая допустимость 415
Оценка максимального правдоподобия (ОМП), примеры неэффективной 399 402
Оценка максимального правдоподобия (ОМП), смещение 311 378
Оценка максимального правдоподобия (ОМП), состоятельность 364 368 372
Оценка максимального правдоподобия (ОМП), сравнение с байесовской оценкой 409
Оценка максимального правдоподобия (ОМП), сравнение с НРМД-оценкой 108 109
Оценка максимального правдоподобия (ОМП), эквивариантность 160 см. «Эффективность
Оценка максимального правдоподобия (ОМП), эффективная второго порядка 311 378
Оценка наименьших квадратов (ОНК) 11 60 134
Оценка наименьших квадратов (ОНК) в линейных моделях 170 173 175 177
Оценка Питмана 148 150 163
Оценка Питмана, асимптотическая эффективность 371 408
Оценка Питмана, допустимость 256
Оценка Питмана, минимаксность 254 408
Оценка Питмана, состоятельность 346
Оценка с постоянным риском 144 155 160 227 249
Оценка Хьюбера 334
Оценка Хьюбера, минимаксность 337
Оценка Хьюбера, сравнение с урезанным средним 338 339
Оценки, связанные с условным математическим ожиданием 81 189
Падманабхан 78 138
Паламадов 87 137
Параметр масштаба 159 210
Параметр сдвига 142 165 210 311
Параметр сдвига в случае многих параметров 278
Параметр сдвига для несимметричного распределения 318 325 см.
Параметризация средним значением в экспоненциальных семействах 113
Параметрическая модель 9 14
Парзен 289
Парк 138
Парные сравнения 345
Пател 138 139
Патил 139
Педерсон 430 471
Пейсаков 210 212 267 286 291
Перлман 373 381 430
Перн 212 256 291
Пинг 244 291
Пирсон 286 290
Пирсон, К. 392 430
Питмен 70 72 112 139 210 212
Питчер 45 72
Плотная последовательность распределений 415
Плотность вероятности 23
Плотность вероятности, оценивание 85 86 98
Плэкет 11 72 185 213
Побочный параметр 399
Поведение «хвостов» распределения 59 312 313 315 316 317 318 324
Подчиненная первого порядка статистика 50
Подчиненная статистика 49 50 70
Пойа 52 73
Показательное распределение 28
Показательное распределение как предельное распределение 402
Показательное распределение, минимальная достаточная статистика для 67
Показательное распределение, отношение к равномерному распределению 67
Показательное распределение, оценивание 89 125 147 167 201 402
Показательное распределение, полные достаточные статистики 51
Полигамма функция 120
| Полиномиальное распределение 34 36 208
Полиномиальное распределение, байесовские и минимаксные оценки 263
Полиномиальное распределение, несмещенные оценки 96 127 186 187 189
Полиномиальное распределение, ОМП 186 392 396
Полнота достаточных статистик 50 68 70
Полнота достаточных статистик в несмещенном оценивании 79 80 134
Полные достаточные статистики в задачах об одной и двух нормальных выборках 83 86
Полные достаточные статистики для выборок из конечной совокупности 191 196
Полные достаточные статистики для двумерного нормального распределения 88
Полные достаточные статистики для непараметрического семейства 68 98 128
Полные достаточные статистики для показательного распределения 51
Полные достаточные статистики для последовательного биномиального выбора 92 126
Полные достаточные статистики для равномерного распределения 50 67
Полные достаточные статистики для экспоненциального семейства 50
Полные достаточные статистики многомерного нормального распределения 88
Положительная часть функции 18
Полфельдт 403 430
Пополнение (меры) 17
Пороговая точка 344 353
Порт 322 355
Портной 109 139 226 291 344 355 395 430
Порядковые статистики 44 47 66 67
Порядковые статистики в задаче о двух выборках 101 128
Порядковые статистики для двумерного распределения 101 128
Порядковые статистики, асимптотическое распределение 350 351
Порядковые статистики, полнота 68 98
Порядковые статистики, распределение 312 см. «Медиана»
Порядок (O, o, 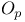 ) 131 347 ) 131 347
Последовательный биномиальный выбор 91 126
Последовательный биномиальный выбор в байесовском оценивании 221
Последовательный биномиальный выбор, минимальная достаточная статистика 126
Последовательный биномиальный выбор, несмещенное оценивание log (p/q) 120
Последовательный биномиальный выбор, несмещенное оценивание p 92
Последовательный биномиальный выбор, несмещенное оценивание pq 127
Последовательный биномиальный выбор, полнота 93 126
Почти всюду (п.в.) 20
Пракаса Рао 398 427
Пратт 88 138 426 430
Прегибон 190 213 396 430
Предельная дисперсия 107 302 347 см.
Предельная риск-эффективность (ПРЭ) 308 347 349
Предельное распределение 298 308 346
Предельный риск-дефект (ПРД) 310 348 349
Приближенная модель 83 334 353
Приближенное значение дисперсии 103
Пробит-анализ 188
Проекция 77 78
Произведение мер 22
Производная Радона — Никодима 22
Производящая функция моментов 36 37
Производящая функция семиинвариантов 36
Пропавшие наблюдения 125
Пропорциональное смещение 194
Простая случайная выборка 191 192 193 195
Простая функция 81
Простой биномиальный выборочный план 92 93
Пуассоновский параметр, байесовская оценка 279
Пуассоновский параметр, допустимые оценки 282
Пуассоновский параметр, минимаксная оценка 249
Пуассоновский параметр, НРМД-оценка 95
Пуассоновский процесс 95
Пукельсгейм 184 207 213
Пфанцагль 33 71 72 82 139 362 378 381 393 409 430
Пфафф 381 431
Пью 139
Рааб 401 428
Равномерно лучшая оценка, несуществование 13
Равномерное распределение 28 42 44 130
Равномерное распределение как предельное унимодальное распределение 318
Равномерное распределение, минимальная достаточная статистика 46 67 68
Равномерное распределение, оценивание 81 125 147 148 162 165 166 349 401
Равномерное распределение, полная достаточная статистика 50 51 68
Равномерное распределение, соотношение с показательным распределением 68
Рагхарачари 246 290
Рагхунанданан 320 322 355
Радхакришнан 265 291
Размер совокупности, оценивание 90
Размерность достаточных статистик 48 70
Размещение Чупрова — Неймана 197
Разность средних значений оценивание 86 87 101 125 153 155 205 345 350
Райфа 286 291
Рамсей 392 429
Рандлс 333 355
Рандомизированная оценка 41 54 55
Рандомизированная оценка в минимаксном оценивании 229 280
Рандомизированная оценка в несмещенном оценивании 124 150
Рандомизированная оценка в эквивариантном оценивании 149 156
Рао, Ж.Н.К. 87 139
Рао, К.Р. 70 72 134 139 147 177 178 184 213 267 291 361 378 409 431
Рао, М.М. 217 289
Рао, П.В. 122 135
Распределение Вейбулла 63 372 387 403
Распределение вероятностей 23 см. «Априорное «Бета-распределение» «Гамма-распределение» «Геометрическое «Дискретное «Двумерное «Двустороннее «Логистическое «Логнормальное «Многомерное «Наименее «Наименее «Нормальное «Показательное «Предельное «Распределение «Распределение «Распределение «Распределение «Распределение «Симметрическое «Строго «t-распределение «Унимодальная «Хи-квадрат
Распределение Дирихле 263
Распределение Коши 12 28 47 61 67 423
Распределение Коши, дисперсия медианы 313 316 351
Распределение Коши, дисперсия урезанного среднего 322
Распределение Коши, информация Фишера 115
Распределение Коши, поведение выборочного среднего 12 61 312
Распределение Коши, порядковые статистики 67 349
Распределение Коши, число корней уравнения правдоподобия 376 420
Распределение Коши, эффективное оценивание 376 387
Распределение логарифмического ряда 65
Распределение Парето 65 402
Распределение Пуассона 33 38 41 131
Распределение Пуассона как не групповое семейство 64
Распределение Пуассона, достаточная статистика 42 44
Распределение Пуассона, информация Фишера 114 131
Распределение Пуассона, моменты 38
Распределение Пуассона, несмещенные оценки 95 109 127
Распределение степенного ряда 65 94
Расслоенная выборка 32 195 197 209
Расслоенный кластер-выбор 199
Регрессия 60 124 168 172 173 278 396
Регрессия в случае, когда обе переменные подвержены ошибкам 400 423
Регрессия гребневая 278
Регрессия, робастное оценивание 345
Регулярный случай, оценивание методом правдоподобия 401 42С
Реднер 363 431
Резников 138
Ридс 376 431
Рихардс 431
Робастность 60 328 344 353
Роббинс 111 122 140
Робертс, А.У. 52 73
Робертс, Д.М. 287
Робинсон 268 291
Роджерс 357
Розенблат 98 139
Рой 139
Ройел 210 213
Роке, А.Ж 327 355
Роке, Д.М. 327 355
Ротенберг 220 291
Рохатги 242 289
Рубин, Д.Б. 87 139 377 426
Рубин, Х. 344 354 428
Рудин 16 52 73
Руперт 327 344 354 355
Рутемиллер 139
Рутковска 263 291
Рухин 78 138
Рыль-Нарджевски 43 71
Сабраманьям 378 409 428
Сава 401 426
Саймонс 123 139
Сакровиц 87 138 429
Сакс 213 232 242 291 333 337 353
Сандберг 377 389 431
Сате 135 139
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 )
)