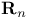|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lee J.M. — Riemannian Manifolds: an Introduction to Curvature |
|
|
 |
| Предметный указатель |
# (sharp) 28—29
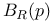 (geodesic ball) 106 (geodesic ball) 106
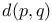 (Riemannian distance) 94 (Riemannian distance) 94
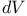 (Riemannian volume element) 29 (Riemannian volume element) 29
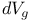 (Riemannian volume element) 29 (Riemannian volume element) 29
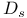 (covariant derivative along transverse curves) 97 (covariant derivative along transverse curves) 97
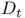 (covariant derivative along a curve) 57 (covariant derivative along a curve) 57
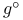 (round metric) 33 (round metric) 33
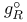 (round metric of radius R) 33 (round metric of radius R) 33
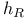 (hyperbolic metric) 38—41 (hyperbolic metric) 38—41
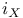 (interior multiplication) 43 (interior multiplication) 43
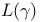 (length of curve) 92 (length of curve) 92
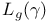 (length of curve) 92 (length of curve) 92
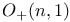 (Lorentz group) 41 (Lorentz group) 41
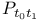 (parallel translation operator) 61 (parallel translation operator) 61
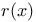 (radial distance function) 77 (radial distance function) 77
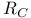 (Ricci tensor) 124 (Ricci tensor) 124
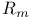 (curvature tensor) 118 (curvature tensor) 118
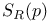 (geodesic sphere) 106 (geodesic sphere) 106
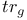 (trace with respect to g) 28 (trace with respect to g) 28
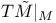 (ambient tangent bundle) 132 (ambient tangent bundle) 132
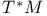 (cotangent bundle) 17 (cotangent bundle) 17
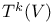 (space of covariant k-tensors) 12 (space of covariant k-tensors) 12
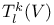 (space of mixed tensors) 12 (space of mixed tensors) 12
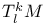 (bundle of mixed tensors) 19 (bundle of mixed tensors) 19
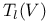 (space of contravariant l-tensors) 12 (space of contravariant l-tensors) 12
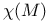 (Euler characteristic) 167 (Euler characteristic) 167
 (Laplacian) 44 (Laplacian) 44
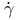 (velocity vector) 56 (velocity vector) 56
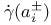 (one-sided velocity vectors) 92 (one-sided velocity vectors) 92
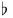 (flat) 27—29 (flat) 27—29
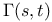 (admissible family) 96 (admissible family) 96
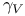 (geodesic with initial velocity V) 59 (geodesic with initial velocity V) 59
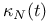 (signed curvature) 163 (signed curvature) 163
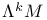 (bundle of k-forms) 20 (bundle of k-forms) 20
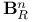 (Poincare ball) 38 (Poincare ball) 38
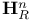 (hyperbolic space) 38—41 (hyperbolic space) 38—41
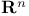 (Euclidean space) 25 33 (Euclidean space) 25 33
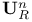 (Poincare half-space) 38 (Poincare half-space) 38
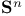 (unit n-sphere) 33 (unit n-sphere) 33
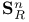 (n-sphere of radius R) 33 (n-sphere of radius R) 33
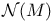 (space of sections of normal bundle) 133 (space of sections of normal bundle) 133
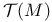 (space of vector fields) 19 (space of vector fields) 19
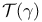 (space of vector fields along a curve) 56 (space of vector fields along a curve) 56
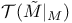 (space of sections of ambient tangent bundle) 133 (space of sections of ambient tangent bundle) 133
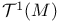 (space of 1-forms) 20 (space of 1-forms) 20
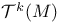 (space of covariant tensor fields) 20 (space of covariant tensor fields) 20
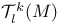 (space of mixed tensor fields) 20 (space of mixed tensor fields) 20
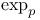 (restricted exponential map) 72 (restricted exponential map) 72
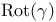 (rotation angle) 156 (rotation angle) 156
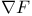 (total covariant derivative) 54 (total covariant derivative) 54
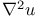 (covariant Hessian) 54 (covariant Hessian) 54
 (tangential connection) 66 135 (tangential connection) 66 135
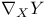 (covariant derivative) 49—50 (covariant derivative) 49—50
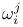 (connection 1-forms) 64 (connection 1-forms) 64
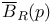 (closed geodesic ball) 106 (closed geodesic ball) 106
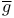 (Euclidean metric) 25 (Euclidean metric) 25
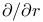 (unit radial vector field) 77 (unit radial vector field) 77
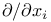 (coordinate vector field) 15 (coordinate vector field) 15
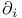 (coordinate vector field) 15 (coordinate vector field) 15
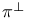 (normal projection) 133 (normal projection) 133
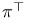 (tangential projection) 133 (tangential projection) 133
 (torsion tensor) 63 68 (torsion tensor) 63 68
 (domain of the exponential map) 72 (domain of the exponential map) 72
Acceleration, Euclidean 48
Acceleration, of a curve on a manifold 58
Acceleration, of a plane curve 3
Acceleration, tangential 48
Adapted orthonormal frame 43 133
Adjoint representation 46
Admissible curve 92
Admissible family 96
Affine connection 51
Aims at a point 109
Algebraic Bianchi identity 122
Alternating tensors 14
Ambient manifold 132
Ambient tangent bundle 132
Ambrose, Cartan — Ambrose — Hicks theorem 205
Angle between vectors 23
Angle tangent 156 157
Angle-sum theorem 2 162 166
Arc length function 93
Arc length parametrization 93
Aspherical 199
Automorphism, inner 46
Ball, geodesic 76 106
Ball, Poincare 38
Base of a vector bundle 16
Berger metrics 151
Berger, Marcel 203
Bi-invariant metric 46 89
Bi-invariant metric, curvature of 129 153
Bi-invariant metric, existence of 46
Bi-invariant metric, exponential map 89
Bianchi identity, algebraic 122
Bianchi identity, contracted 124
Bianchi identity, differential 123
Bianchi identity, first 122
Bianchi identity, second 123
Bonnet, Bonnet's theorem 9 200
Bonnet, Gauss — Bonnet theorem 167
Boundary problem, two-point 184
Bundle, cotangent 17
Bundle, normal 17 133
Bundle, of k-forms 20
Bundle, of tensors 19
Bundle, tangent 17
Bundle, vector 16
Calculus of variations 96
Caratheodory metric 32
Carnot — Caratheodory metric 31
Cartan — Ambrose — Hicks theorem 205
Cartan — Hadamard manifold 199
Cartan — Hadamard theorem 9 196
Cartan's first structure equation 64
Cartan's second structure equation 128
Catenoid 150
Cayley transform 40
Cayley transform, generalized 40
Chern — Gauss — Bonnet theorem 170
Christoffel symbols 51
Christoffel symbols, formula in coordinates 70
Circle classification theorem 2
circles 2
Circumference theorem 2 162 166
Classification Theorem 2
Classification theorem, circle 2
Classification theorem, constant curvature metrics 9 206
Classification theorem, plane curve 4
Closed curve 156
Closed geodesic ball 76
Coframe 20
Commuting vector fields, normal form 121
Comparison theorem, conjugate point 195
Comparison theorem, Jacobi field 194
Comparison theorem, metric 196
Comparison theorem, Rauch 203 204
Comparison theorem, Sturm 194
Compatibility with a metric 67
Complete, geodesically 108
Complex projective space 46
Conformal metrics 35
Conformally equivalent 35
Conformally flat, hyperbolic space 41
Conformally flat, locally 37
Conformally flat, sphere 37
Congruent 2
conjugate 182
Conjugate locus 190
| Conjugate point 182
Conjugate point, comparison theorem 195
Conjugate point, geodesic not minimizing past 188
Conjugate point, singularity of expp 182
Connection 49
Connection 1-forms 166
Connection, 1-forms 64 165
Connection, Euclidean 52
Connection, existence of 52
Connection, formula in arbitrary frame 69
Connection, formula in coordinates 70
Connection, in a vector bundle 49
Connection, in components 51
Connection, linear 51
Connection, naturality 70
Connection, on tensor bundles 53—54
Connection, Riemannian 68
Connection, tangential 66
Constant Gaussian curvature 7
Constant sectional curvature 148
Constant sectional curvature, classification 9 206
Constant sectional curvature, formula for curvature tensor 148
Constant sectional curvature, formula for metric 179
Constant sectional curvature, local uniqueness 181
Constant sectional curvature, model spaces 9
Constant sectional curvature, uniqueness 204
Constant speed curve 70
Contracted Bianchi identity 124
Contraction 13
Contravariant tensor 12
Control theory 32
Converge to infinity 113
Convex geodesic polygon 171
Convex set 112
coordinates 14
Coordinates, have upper indices 15
Coordinates, local 14
Coordinates, normal 77
Coordinates, Riemannian normal 77
Coordinates, slice 15
Coordinates, standard, on 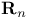 25 25
Coordinates, standard, on tangent bundle 19
Cosmological constant 126
Cotangent bundle 17
Covariant derivative 50
Covariant derivative, along a curve 57—58
Covariant derivative, of tensor field 53—54
Covariant derivative, total 54
Covariant Hessian 54 63
Covariant tensor 12
Covectors 11
Covering map 197
Covering metric 27
Covering Riemannian 27
Covering transformation 27
Critical point 101 126 142
Crystallographic groups 206
Curvature 3—10 117
Curvature, 2-forms 128
Curvature, constant sectional 9 148 179—181 204 206
Curvature, constant, formula for 148
Curvature, endomorphism 117 128
Curvature, Gaussian 6—7 142—145
Curvature, geodesic 137
Curvature, in coordinates 128
Curvature, mean 142
Curvature, of a curve in a manifold 137
Curvature, of a plane curve 3
Curvature, principal 4 141
Curvature, Ricci 124
Curvature, Riemann 117 118
Curvature, scalar 124
Curvature, sectional 9 146
Curvature, signed 4 163
Curvature, tensor 118
Curve 55
Curve, admissible 92
Curve, in a manifold 55
Curve, plane 3
Curve, segment 55
Curved polygon 157 162
Cusp 157
Cut locus 190
Cut point 190
Cylinder, principal curvatures 5
Deck transformation 27
Defining function 150
Diameter 199
Difference tensor 63
Differential Bianchi identity 123
Differential forms 20
Dihedral groups 206
Distance, Riemannian 94
Divergence 43
Divergence, in terms of covariant derivatives 88
Divergence, operator 43
Divergence, Theorem 43
Domain of the exponential map 72
Dual basis 13
Dual coframe 20
Dual space 11
E(n) (Euclidean group) 44
Edges of a curved polygon 157
Eigenfunction of the Laplacian 44
Eigenvalue of the Laplacian 44
Einstein field equation 126
Einstein general theory of relativity 31 126
Einstein metric 125 202
Einstein special theory of relativity 31
Einstein summation convention 13
Embedded submanifold 15
Embedding 15
Embedding, isometric 132
End(V) (space of endomorphisms) 12
Endomorphism curvature 117
Endomorphism of a vector space 12
Escape lemma 60
Euclidean acceleration 48
Euclidean connection 52
Euclidean geodesics 81
Euclidean group 44
Euclidean homogeneous and isotropic 45
Euclidean metric 25 33
Euclidean triangle 2
Euler characteristic 167 170
Euler — Lagrange equation 101
Existence and uniqueness for linear ODEs 60
Existence and uniqueness for ODEs 58
Existence and uniqueness of geodesics 58
Existence and uniqueness of Jacobi fields 176
exp (exponential map) 72
Exponential map 72
Exponential map, domain of 72
Exponential map, naturality 75
Exponential map, of bi-invariant metric 89
Extendible vector fields 56
Extension of functions 15
Extension of vector fields 16 132
Exterior angle 157 163
Exterior k-form 14
Family, admissible 96
Fiber metric 29
Fiber of a submersion 45
Fiber of a vector bundle 16
Finsler metric 32
First Bianchi identity 122
First fundamental form 134
First structure equation 64
First variation 99
Fixed-endpoint variation 98
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



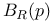 (geodesic ball)
(geodesic ball) 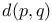 (Riemannian distance)
(Riemannian distance) 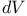 (Riemannian volume element)
(Riemannian volume element) 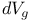 (Riemannian volume element)
(Riemannian volume element) 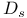 (covariant derivative along transverse curves)
(covariant derivative along transverse curves) 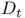 (covariant derivative along a curve)
(covariant derivative along a curve) 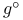 (round metric)
(round metric) 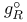 (round metric of radius R)
(round metric of radius R) 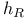 (hyperbolic metric)
(hyperbolic metric) 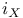 (interior multiplication)
(interior multiplication) 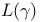 (length of curve)
(length of curve) 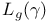 (length of curve)
(length of curve) 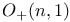 (Lorentz group)
(Lorentz group) 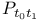 (parallel translation operator)
(parallel translation operator) 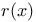 (radial distance function)
(radial distance function) 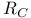 (Ricci tensor)
(Ricci tensor) 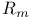 (curvature tensor)
(curvature tensor) 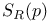 (geodesic sphere)
(geodesic sphere) 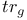 (trace with respect to g)
(trace with respect to g) 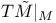 (ambient tangent bundle)
(ambient tangent bundle) 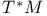 (cotangent bundle)
(cotangent bundle) 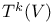 (space of covariant k-tensors)
(space of covariant k-tensors) 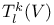 (space of mixed tensors)
(space of mixed tensors) 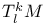 (bundle of mixed tensors)
(bundle of mixed tensors) 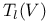 (space of contravariant l-tensors)
(space of contravariant l-tensors) 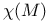 (Euler characteristic)
(Euler characteristic)  (Laplacian)
(Laplacian) 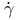 (velocity vector)
(velocity vector) 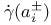 (one-sided velocity vectors)
(one-sided velocity vectors) 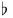 (flat)
(flat) 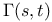 (admissible family)
(admissible family) 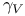 (geodesic with initial velocity V)
(geodesic with initial velocity V) 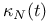 (signed curvature)
(signed curvature) 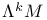 (bundle of k-forms)
(bundle of k-forms) 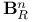 (Poincare ball)
(Poincare ball) 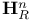 (hyperbolic space)
(hyperbolic space) 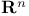 (Euclidean space)
(Euclidean space) 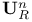 (Poincare half-space)
(Poincare half-space) 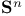 (unit n-sphere)
(unit n-sphere) 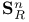 (n-sphere of radius R)
(n-sphere of radius R) 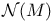 (space of sections of normal bundle)
(space of sections of normal bundle) 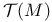 (space of vector fields)
(space of vector fields) 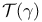 (space of vector fields along a curve)
(space of vector fields along a curve) 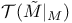 (space of sections of ambient tangent bundle)
(space of sections of ambient tangent bundle) 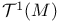 (space of 1-forms)
(space of 1-forms) 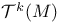 (space of covariant tensor fields)
(space of covariant tensor fields) 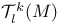 (space of mixed tensor fields)
(space of mixed tensor fields) 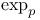 (restricted exponential map)
(restricted exponential map) 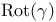 (rotation angle)
(rotation angle) 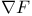 (total covariant derivative)
(total covariant derivative) 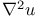 (covariant Hessian)
(covariant Hessian)  (tangential connection)
(tangential connection) 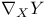 (covariant derivative)
(covariant derivative) 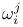 (connection 1-forms)
(connection 1-forms) 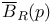 (closed geodesic ball)
(closed geodesic ball) 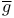 (Euclidean metric)
(Euclidean metric) 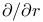 (unit radial vector field)
(unit radial vector field) 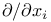 (coordinate vector field)
(coordinate vector field) 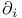 (coordinate vector field)
(coordinate vector field) 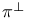 (normal projection)
(normal projection) 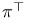 (tangential projection)
(tangential projection)  (torsion tensor)
(torsion tensor)  (domain of the exponential map)
(domain of the exponential map)