|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lee J.M. — Riemannian Manifolds: an Introduction to Curvature |
|
|
 |
| Предметный указатель |
Flat (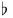 ) 27—29 ) 27—29
Flat connection 128
Flat locally conformally 37
Flat Riemannian metric 24 119
Flatness criterion 117
Forms, bundle of 20
Forms, differential 20
Forms, exterior 14
Frame, local 20
Frame, orthonormal 24
Fubini — Study metric 46 204
Fubini — Study metric, curvature of 152
Functional, length 96
Functional, linear 11
Fundamental form, first 134
Fundamental form, second 134
Fundamental lemma of Riemannian geometry 68
Gauss equation 136
Gauss equation for Euclidean hypersurfaces 140
Gauss formula 135
Gauss formula along a curve 138
Gauss formula for Euclidean hypersurfaces 140
Gauss lemma 102
Gauss map 151
Gauss — Bonnet formula 164
Gauss — Bonnet theorem 7 167
Gauss — Bonnet, Chern — Gauss — Bonnet theorem 170
Gauss's Theorema Egregium 6 143
Gaussian curvature 6 142
Gaussian curvature, constant 7
Gaussian curvature, is isometry invariant 143
Gaussian curvature, of abstract 2-manifold 144
Gaussian curvature, of hyperbolic plane 145
Gaussian curvature, of spheres 142
General relativity 31 126
Generalized Cayley transform 40
Generating curve 87
Genus 169
Geodesic ball 76 106
Geodesic closed 76
Geodesic curvature 137
Geodesic equation 58
Geodesic polygon 171
Geodesic sphere 76 106
Geodesic triangle 171
Geodesic vector field 74
Geodesically complete 108
Geodesically complete, equivalent to metrically complete 108
Geodesics 8 58
Geodesics, are constant speed 70
Geodesics, are locally minimizing 106
Geodesics, existence and uniqueness 58
Geodesics, maximal 59
Geodesics, on Euclidean space 58 81
Geodesics, on hyperbolic spaces 83
Geodesics, on spheres 82
Geodesics, radial 78 105
Geodesics, Riemannian 70
Geodesics, with respect to a connection 58
Gradient 28
Gram — Schmidt algorithm 24 30 43 143 164
Graph coordinates 150
Great circles 82
Great hyperbolas 84
Green's identities 44
H (mean curvature) 142
h (scalar second fundamental form) 139
Hadamard, Cartan — Hadamard theorem 196
Half-cylinder, principal curvatures 5
Half-plane, upper 7
Half-space, Poincar?e 38
Harmonic function 44
Hausdorff 14
Hessian covariant 54 63
Hessian of length functional 187
Hicks, Cartan — Ambrose — Hicks theorem 205
Hilbert action 126
Homogeneous and isotropic 33
Homogeneous Riemannian manifold 33
Homotopy groups, higher 199
Hopf — Rinow theorem 108
Hopf, Heinz 158
Hopf, rotation angle theorem 158
Hopf, Umlaufsatz 158
Horizontal index position 13
Horizontal lift 45
Horizontal space 45
Horizontal vector field 89
Hyperbolic metric 38—41
Hyperbolic plane 7
Hyperbolic space 38—41
Hyperbolic stereographic projection 38
Hyperboloid model 38
Hypersurface 139
I(V, W) (index form) 187
Ideal triangle 171
Identification, 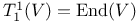 12 12
Identification, 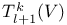 with multilinear maps 12 with multilinear maps 12
II (second fundamental form) 134
Immersed submanifold 15
Immersion 15
Immersion, isometric 132
Index form 187
Index of a geodesic segment 189
Index of pseudo-Riemannian metric 30 43
Index position 13
Index raising and lowering 28
Index summation convention 13
Index upper and lower 13
Index upper, on coordinates 15
Induced metric 25
Inertia, Sylvester's law of 30
Inner automorphism 46
Inner product 23
Inner product on tensor bundles 29
Inner product on vector bundle 29
Integral of a function 30
Integral with respect to arc length 93
Integration by parts 43 88
Interior angle 2
Interior multiplication 43
Intrinsic property 5
Invariants, local 115
Inward-pointing normal 163
Isometric embedding 132
Isometric immersion 132
Isometric locally 115
Isometric manifolds 24
Isometries of Euclidean space 44 88
Isometries of hyperbolic spaces 41—42 88
Isometries of spheres 33—34 88
Isometry 5 24
Isometry group 24
Isometry group of Euclidean space 44 88
Isometry group of hyperbolic spaces 41—42 88
Isometry group of spheres 33—34 88
Isometry, group See Isometry group
Isometry, local 115 197
Isometry, metric 112
Isometry, of M 24
Isometry, Riemannian 112
Isotropic at a point 33
Isotropic homogeneous and 33
Isotropy subgroup 33
Jacobi equation 175
Jacobi field 176
Jacobi field, comparison theorem 194
Jacobi field, existence and uniqueness 176
Jacobi field, in normal coordinates 178
Jacobi field, normal 177
| Jacobi field, on constant curvature manifolds 179
Jumps in tangent angle 157
K (Gaussian curvature) 142
Kazdan, Jerry 169
Klingenberg, Walter 203
Kobayashi metric 32
Laplacian 44
Latitude circle 87
Law of inertia, Sylvester's 30
Left-invariant metric 46
Left-invariant metric, Christoffel symbols 89
Length functional 96
Length of a curve 92
Length of tangent vector 23
Lens spaces 206
Levi — Civita connection 68
Lie derivative 63
Linear connection 51
Linear functionals 11
Linear ODEs 60
Local coordinates 14
Local frame 20
Local frame, orthonormal 24
Local invariants 115
Local isometry 88 115 197
Local parametrization 25
Local trivialization 16
Local uniqueness of constant curvature metrics 181
Local-global theorems 2
Locally conformally flat 37
Locally conformally flat, hyperbolic space 41
Locally conformally flat, sphere 37
Locally minimizing curve 106
Lorentz group 41
Lorentz metric 30
Lowering an index 28
Main curves 96
Manifold, Riemannian 1 23
Maximal geodesic 59
Mean curvature 142
Meridian 82 87
Metric, Berger 151
Metric, bi-invariant 46 89 129 153
Metric, Caratheodory 32
Metric, Carnot — Caratheodory 31
Metric, comparison theorem 196
Metric, Einstein 125 202
Metric, Euclidean 25 33 45
Metric, fiber 29
Metric, Finsler 32
Metric, Fubini — Study 46 152 204
Metric, hyperbolic 38—41
Metric, induced 25
Metric, isometry 112
Metric, Kobayashi 32
Metric, Lorentz 30
Metric, Minkowski 31 38
Metric, on submanifold 25
Metric, on tensor bundles 29
Metric, product 26
Metric, pseudo-Riemannian 30 43
Metric, Riemannian 1 23
Metric, round 33
Metric, semi-Riemannian 30
Metric, singular Riemannian 31
Metric, space 94
Metric, sub-Riemannian 31
Minimal surface 142
Minimizing curve 96
Minimizing curve is a geodesic 100 107
Minimizing curve, locally 106
Minkowski metric 31 38
Mixed tensor 12
Model spaces 9 33
Morse index theorem 189 204
Multilinear over 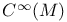 21 21
Multiplicity of conjugacy 182
Myers's theorem 201
Nash embedding theorem 66
Naturality of the exponential map 75
Naturality of the Riemannian connection 70
NM (normal bundle) 132
Nondegenerate 2-tensor 30 116
Nonvanishing vector fields 115
Norm Finsler metric 32
Norm of tangent vector 23
Normal bundle 17 133
Normal coordinates, Riemannian 77
Normal form for commuting vector fields 121
Normal Jacobi field 177
Normal neighborhood 76
Normal neighborhood lemma 76
Normal projection 133
Normal space 132
Normal vector field along a curve 177
O(n+1) (orthogonal group) 33
O(n,1) (Lorentz group) 41
One-sided derivatives 55
One-sided velocity vectors 92
Order of conjugacy 182
Orientation, for curved polygon 157
Orthogonal 24
Orthogonal group 33
Orthonormal 24
Orthonormal, frame 24
Orthonormal, frame, adapted 43 133
Osculating circle 3 137
Pairing between V and 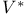 11 11
Parallel translation 60—62 94
Parallel vector field 59 87
Parametrization by arc length 93
Parametrization of a surface 25
Parametrized curve 55
Partial derivative operators 15
Partition of unity 15 23
Path-lifting property 156 197
Pfaffian 170
Piecewise regular curve 92
Piecewise smooth vector field 93
Pinching theorems 203
Plane curve 3
Plane curve classification theorem 4
Plane section 145
Poincare ball 38
Poincare half-space 38
Polygon, curved 157 162
Polygon, geodesic 171
Positive definite 23
Positively oriented curved polygon 157 163
Principal curvatures 4 141
Principal directions 141
Product metric 26
Product rule for connections 50
Product rule for divergence operator 43
Product rule for Euclidean connection 67
Projection, hyperbolic stereographic 38
Projection, normal 133
Projection, of a vector bundle 16
Projection, stereographic 35
Projection, tangential 133
Projective space, complex 46
Projective space, real 148
Proper variation 98
Proper vector field along a curve 98
Pseudo-Riemannian metric 30
Pullback connection 71
R (curvature endomorphism) 117
Radial distance function 77
Radial geodesics 78
Radial geodesics are minimizing 105
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



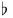 )
) 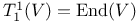
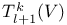 with multilinear maps
with multilinear maps