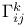|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Lee J.M. — Riemannian Manifolds: an Introduction to Curvature |
|
|
 |
| Предметный указатель |
Radial vector field, unit 77
Rado, Tibor 167
Raising an index 28
Rank of a tensor 12
Rauch comparison theorem 203 204
Real projective space 148
Regular curve 92
Regular submanifold 15
Relativity, general 31 126
Relativity, special 31
Reparametrization 92
Reparametrization of admissible curve 93
Rescaling lemma 73
Restricted exponential map 72
Ricci curvature 124
Ricci identity 128
Ricci tensor 124
Ricci tensor, geometric interpretation 147
Ricci tensor, symmetry of 124
Riemann curvature endomorphism 117
Riemann curvature tensor 118
Riemann, G.F.B. 32
Riemannian connection 68—71
Riemannian covering 27
Riemannian distance 94
Riemannian geodesics 70
Riemannian isometry 112
Riemannian manifold 1 23
Riemannian metric 1 23
Riemannian normal coordinates 77
Riemannian submanifold 132
Riemannian submersion 45—46 89
Riemannian volume element 29
Right-invariant metric 46
Rigid motion 2 44
Robot arm 32
Rotation angle 156
Rotation angle of curved polygon 158 163
Rotation angle theorem 158
Rotation angle theorem for curved polygon 163
Round metric 33
S (scalar curvature) 124
s (shape operator) 140
scalar 139—140
Scalar curvature 124
Scalar curvature, geometric interpretation 148
Scalar second fundamental form 139
Scalar second fundamental form, geometric interpretation 140
Schoen, Richard 127
Secant angle function 159
Second Bianchi identity 123
Second countable 14
Second fundamental form 134
Second fundamental form, geometric interpretation 138 140
Second structure equation 128
Second variation formula 185
Section of a vector bundle 19
Section of a vector bundle, zero section 19
Sectional curvature 9 146
Sectional curvature of Euclidean space 148
Sectional curvature of hyperbolic spaces 148 151
Sectional curvature of spheres 148
Sectional curvature, constant 148
Sections, space of 19
Segment, curve 55
Semi-Riemannian metric 30
Semicolon between indices 55
Shape operator 140
Sharp (#) 28—29
Sides of a curved polygon 157
Sign conventions for curvature tensor 118
Signed curvature 4
Signed curvature of curved polygon 163
Simple curve 156
Singular Riemannian metric 31
Singularities of the exponential map 182
SL(2, R) (special linear group) 45
Slice coordinates 15
Smooth 14
Space forms 206—207
Special relativity 31
Speed of a curve 70
Sphere 33
Sphere theorem 203
Sphere, geodesic 76 106
Sphere, homogeneous and isotropic 34
Sphere, principal curvatures of 6
Spherical coordinates 82
SSS theorem 2
Standard coordinates on 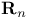 25 25
Standard coordinates tangent bundle 19
Star-shaped 72 73
Stereographic projection 35
Stereographic projection is a conformal equivalence 36
Stereographic projection, hyperbolic 38
Stokes's theorem 157 165
Stress-energy tensor 126
Structure constants of Lie group 89
Structure equation, first 64
Structure equation, second 128
Sturm comparison theorem 194 208
Sturm separation theorem 208
SU(2) (special unitary group) 151
Sub-Riemannian metric 31
Subdivision of interval 92
Submanifold 15
Submanifold, embedded 15
Submanifold, immersed 15
| Submanifold, regular 15
Submanifold, Riemannian 25 132
Submersion, Riemannian 45—46 89
Summation convention 13
Surface of revolution 25 87
Surface of revolution, Gaussian curvature 150
Surfaces in space 4
Sylvester's law of inertia 30
Symmetric 2-tensor 23
Symmetric connection 63 68
Symmetric product 24
Symmetries of Euclidean space 44 88
Symmetries of hyperbolic spaces 41—42 88
Symmetries of spheres 33—34 88
Symmetries of the curvature tensor 121
Symmetry lemma 97
Symplectic forms 116
Tangent angle function 156 157 163
Tangent bundle 17
Tangent space 15
Tangential acceleration 48
Tangential connection 66 135
Tangential projection 133
Tangential vector field along a curve 177
Tensor bundle 19
Tensor characterization lemma 21
Tensor contravariant 12
Tensor covariant 12
Tensor field 20
Tensor fields, space of 20
Tensor mixed 12
Tensor of type 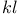 12 12
Tensor on a manifold 19
Tensor product 12
Theorema egregium 6 143
TM (tangent bundle) 17
Torsion 2-forms 64
Torsion tensor 63 68
Torus, n-dimensional 25 27
Total covariant derivative 54
Total covariant derivative, components of 55
Total curvature theorem 4 162 166
Total scalar curvature functional 126 127
Total space of a vector bundle 16
Totally awesome theorem 6 143
Totally geodesic 139
Trace of a tensor 13
Trace with respect to g 28
Transformation law for 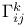 63 63
Transition function 18
Translation, parallel 60—62
Transverse curves 96
Triangle, Euclidean 2
Triangle, geodesic 171
Triangle, ideal 171
Triangulation 166 171
Trivialization, local 16
Tubular neighborhood theorem 150
Two-point boundary problem 184
Umlaufsatz 158
Uniformization theorem 7
Uniformly normal 78
Uniqueness of constant curvature metrics 181
Unit radial vector field 77
Unit speed curve 70
Unit speed parametrization 93
Upper half-plane 7 45
Upper half-space 38
Upper indices on coordinates 15
Vacuum Einstein field equation 126
Variation, field 98
Variation, first 99
Variation, fixed-endpoint 98
Variation, of a geodesic 98
Variation, proper 98
Variation, second 185
Variation, through geodesics 174
Variational equation 101
Variations, calculus of 96
Vector bundle 16
Vector bundle, section of 19
Vector bundle, space of sections 19
Vector bundle, zero section 19
Vector field 19
Vector field along a curve 56
Vector field along an admissible family 96
Vector field, normal, along a curve 177
Vector field, piecewise smooth 93
Vector field, proper 98
Vector field, tangential, along a curve 177
Vector fields, commuting 121
Vector fields, space of 19
Vector space, tensors on 12
Velocity 48 56
Vertical index position 13
Vertical space 45
Vertical vector field 89
Vertices of a curved polygon 157
Volume 30
Volume element 29
Warner, Frank 169
Wedge product 14
Wedge product, alternative definition 14
Weingarten equation 136
Weingarten equation for Euclidean hypersurfaces 140
Wolf, Joseph 206
Yamabe problem 127
Zero section 19
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте