|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Burton D.M. — Elementary Number Theory |
|
|
 |
| Предметный указатель |
Seeds (autokey cryptosystems) 200
Selberg, Atle (1917—) 352 378
Selfridge, John 240
Shamir, Adir 203 212
Sieve of Eratosthenes 44—45
Signatures for encrypted messages 215—216
Simple finite continued fractions, defined 307 (see also “Finite continued fractions”)
Simple infinite continued fractions, defined 321 322
Simultaneous linear congruences 78—79
Single linear congruences 76—78
Skewes number 377
Skewes, S. 377
Smallest positive primitive roots 156 393
Sociable chains 236
Sophia Dorothea (Queen Mother of Prussia) 130
Square roots (continued fractions method) 307
Square-free numbers 43 91
Square-full numbers 43
Square/rectangle Fibonacci number problem 293—294
Steuerwald, R. 231
Strong pseudoprime numbers 367
Subset sum problems see “Knapsack problems”
Sum of cubes 278
Sum of divisors  as multiplicative function 108 109—110 as multiplicative function 108 109—110
Sum of divisors  , amicable pairs and 233 , amicable pairs and 233
Sum of divisors  , basic properties 103—107 , basic properties 103—107
Sum of divisors  , greatest integer function and 120 , greatest integer function and 120
Sum of divisors  , table of 407—408 , table of 407—408
Sum of fifth powers 278 279
Sum of four squares 263 273—277
Sum of fourth powers 278 279
Sum of n nth powers 279
Sum of three squares 272—273
Sum of two cubes 272
Sum of two squares 264—269
Sums of Fibonacci numbers 295—296
Sun-Tsu (c.250 a.d.) 79 80
Superincreasing sequences 209
Superperfect numbers 225
Sylvester, James Joseph (1814—1897) 57 233
Synopsis of Pure Mathematics (Carr) 303
Tchebychef, P. L. (1821—1894) 48 52 374
te Riele, Herman J. 116
Thabit ibn Qurrah (c.836—901) 234
The Gold Bug (Poe) 198—199
Theon of Alexandria (4th century a.d.) 15
Theorie des Fonctions Analytique (Lagrange) 263
Theorie des Nombres (Legendre) 175 357
Theorie des Nombres (Lucas) 363
Theory of Numbers (Barlow) 229
Three-primes problem 351
Thue, Alex (1863—1922) 264
Thue’s lemma 264—265
Tijdeman, R. 258
Torricelli, Evangelista (1608—1647) 218
| Totient see “Euler’s phi-function”
Traicte de Chiffres (Vigenere) 199
Traite du Triangle Arithmetique (Pascal) 10
Triangles, Pascal’s 9
Triangles, Pythagorean 250 257
Triangular numbers in Pythagorean triangles 257
Triangular numbers, defined 15
Triangular numbers, facts 15—16
Triangular numbers, Fibonacci numbers 295
Trivium 13
Tsu Chung-chi (430—501) 332
Turcaninov, A. 233
Twin primes, convergence of 375
Twin primes, defined 50
Twin primes, table of numbers of 406
Uber die Anzahl der Primzahlen unter einer gegebenen Grosse (Riemann) 375
Uniqueness of infinite continued fractions 323—324 326
Uniqueness of prime factorization 41
Universal exponent 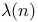 162 162
Utriusque Arithmetices (Regius) 222
Vallee-Poussin, Charles-Jean de la (1866—1962) 376
vbasis for induction 4
Verman cryptosystem 202—203
Verman, Gilberts. 202
Vigenere cryptosystem 199—200
Vigenere, Blaise de (1523—1596) 199 200
Vinogradov, Ivan Matveyevich (1891—1983) 52 351
Wagstaff, Samuel S. 255
Wallis, John (1616—1703), infinite product for  320 320
Wallis, John (1616—1703), Pell’s equation and 334—336
Waring, Edward (1734—1798) 93—94 277
Waring’s problem 277—279 350—351
Weekday number, determining 125—126
Weighting schemes for check digits 73
Well-ordering principle 1—2
Western, Alfred E. (1873—1961) 239 240
Wieferich primes 258
Wieferich, Arthur 258
Wiles, Andrew (1953—) 255
Williams, H. C 356
Wilson, John (1741—1793) 93
Wilson’s theorem, citations 173
Wilson’s theorem, defined 93—95
Wilson’s theorem, Lagrange’s theorem and 154
Wilson’s theorem, quadratic congruences and 95—96
Wolf Prize 352
Word problems see “Puzzle problems”
Xylander (1532—1576) 86
Yen Kung (14th century) 38
Yih-hing(d. 717) 83
Zeckendorf representation 295—296
Zero, congruence to 67
Zeros of the Zeta Function 376
Zeta function 373 376
“Recherches d’Analyse Indeterminee” (Legendre) 175
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 as multiplicative function
as multiplicative function