Авторизация
Поиск по указателям
Rotman J.J. — An Introduction to the Theory of Groups
Обсудите книгу на научном форуме Нашли опечатку?
Название: An Introduction to the Theory of GroupsАвтор: Rotman J.J. Аннотация: Anyone who has studied abstract algebra and linear algebra as an undergraduate can understand this book. This edition has been completely revised and reorganized, without however losing any of the clarity of presentation that was the hallmark of the previous editions.The first six chapters provide ample material for a first course: beginning with the basic properties of groups and homomorphisms, topics covered include Lagrange's theorem, the Noether isomorphism theorems, symmetric groups, G-sets, the Sylow theorems, finite Abelian groups, the Krull-Schmidt theorem, solvable and nilpotent groups, and the Jordan-Holder theorem.The middle portion of the book uses the Jordan-Holder theorem to organize the discussion of extensions (automorphism groups, semidirect products, the Schur-Zassenhaus lemma, Schur multipliers) and simple groups (simplicity of projective unimodular groups and, after a return to G-sets, a construction of the sporadic Mathieu groups).
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1995Количество страниц: 513Добавлена в каталог: 09.12.2006Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
415 152 151 153 151 152 152 110 110 236 Aanderaa, S. 450 Abbati, P. 1 57 58 Abel, N.H. 1 97 Abelian group 13 ACC 145 action 55 Adding a handle 409 Adian — Rabin theorem 469 Adian, S.I. 136 adjacency 174 Adjoining roots 92 Adjoint transformation 242 Admissible subgroup 151 Affine group Aff(n, k) 264 Affine group of the plane 71 Affine hyperplane 265 Affine isomorphism 266 Affine line 265 Affine m-subspace 265 Affine map 70 Affine n-space 265 Affinity 264 Alperin — Kuo theorem 210 Alphabet of Turing machine 421 Alternating bilinear form 235 Alternating group, 23 Alternating group, infinite a.g. 51 Amalgam 401 Artin, E. 227: 347 Ascending central series 113 Ascending chain condition 145 Associated graph to directed graph 356 Associated semigroup to Turing machine 426 Associated vector space to affine space 265 Associativity 10 Associativity, generalized 11 Attaching a 2-cell along 398 Attaching map 398 Automorphism, field 93 Automorphism, graph 174 Automorphism, group 104 156 Automorphism, Steiner system 295 Automorphism, tower 163 Auxiliary table 352 Axiom of Choice 481 Baer theorem 320 Baer — Levi theorem 391 Baer, R. 111 327 334 350 383 Balanced group 365 Base, HNN extension 407 411 Base, wreath product 172 Basepoint 370 Basic move of Turing machine 421 Basic subgroup 326 Basis, free abelian group 312 Basis, free group 343 Basis, free semigroup 349 Basis, theorem 128 319 447 Bijection 480 Bilinear form 235 Bilinear form, alternating 235 Bilinear form, symmetric 235 Binary tetrahedral group 350 Block, G-set 256 Block, nontrivial 256 Block, Steiner system 293 Boone theorem 417 Boone — Higman theorem 466 Boone's lemma 431 Boone, W.W. 430 450 Both chain conditions 146 Boundary word 435 Bouquet of circles 377 Braid group 347 Brandis, A. 210 Britton's lemma 414 Britton, J.L. 430 Bruck — Ryser Theorem 294 Burnside Basis Theorem 124 Burnside lemma 58 Burnside normal complement theorem 196 Burnside problem 136 Burnside theorem 107 110 Cameron, P.l. 286 Cancellation law 5 15 Cardano, G. 90 Carmichael — Witt theorem 297 Carmichael, R. 35 Cassidy, P.I. 34 Cauchy theorem 102 Cauchy, A.L. 1 4 Cayley 34 Cayley graph 357 Cayley theorem 52 Center 44 CenterIess 45 Central extension 201 Central isomorphism 151 Central series 117 Centralizer element 44 Centralizer subgroup 112 Centralizes 112 Chain conditions see ACC DCC or Character group 205 340 Characteristic, abelian group of rank 1 332 Characteristic, field 218 Characteristic, subgroup 104 Characteristically simple 106 Chevalley groups 246 Chief series 152 Chinese remainder theorem for G-sets 260 Church's thesis 423 Circle group T 18 Circuit 371 Class equation 74 Class of nilpotency 115 Classical groups 239 Classification theorem of finite simple groups 246 Closed path 368 Coboundary 183 Cocycle 180 Cocycle, identity 180 Cohomology group, first 212 Cohomology group, second 183 Cole, F.N. 225 292 Collapse 354 Collapse, double 31 Collapse, enumeration 354 Collineation 274 Collins, D.l. 430 Coloring 60 Common system of representatives 25 Commutative diagram 183 Commutator 33 Commutator, identities 119 Commutator, subgroup 33 Commute 5 Companion matrix 138 Complement 167 Complete factorization 6 Complete group 158 Complete set of coset representatives = transversal 178 Complete wreath product 175 COMPLEX 366 Complex, components 369 Complex, connected 368 Complex, covering 377 Complex, dimension 367 Complex, edge 367 Complex, isomorphic 371 Complex, pointed 370 Complex, quotient 373 Complex, simply connected 372 Complex, tree 372 Complex, universal covering 383 Complex, vertices 366 Complex, wedge 399 Components of complex 369 Composition factors 101 Composition series 98 Computation of Turing machine 422 Congruence class 13 Congruence on semigroup 349 Congruent matrices 236 Congruent matrices, 236 Conjugacy class 43 Conjugate elements 31 43 Conjugate elements, subgroups 44 Conjugation 18 Connected complex 368 Continuation 381 Contraction of Steiner system 294 Contravariant functor 336 Convex combination 70 Corner, A.L.S. 334 Correspondence theorem 38 Coset 4 Countable 484 Counting principle 294 Covariant functor 335 Cover group 208 Covering complex 377 Covering map 382 Coxeter, H.S.M. 351 Crossed homomorphism 211 Cubic formula 90 CYCLE 3 Cycle, index 60 Cycle, structure, same 46 Cyclic group 21 Cyclic permutation of word 434 Cyclic subgroup 21 Cyclic submodule 135 Cyclically reduced word 434 DATA 179 DCC 146 Decision process 418 Dedekind law 37 Degree, field extension 93 Degree, G-set 55 Degree, vertex in graph 358 Dehn, M. 430 Derivation 211 Derived series 104 Derived subgroup = commutator subgroup 33 Descartes, R. 90 Descending central series 113 Descending chain condition 146 Diagram 435 Diagram, commutative 183 Dickson, L.E. 232 246 Dicyclic group 351 Dihedral group 68 Dilatation 228 Dimension, affine space 265 Dimension, complex 367 Dimension, projective space 273 Dimension, simplex 366 Direct factor 126 Direct product, 40 Direct product, infinite 308 Direct sum, infinite 308 Direct sum, matrices 138 Direct sum, modules 135 Direct summand 126 308 Directed graph 356 Directed polygon 433 Directed polygon, labeled directed polygon 433 Dirichlet, P.G.L. 200 Disjoint permutations 5 Disjoint subcomplexes 368 Divisible by n 309 Divisible group 207 320 Division algorithm 486 Double coset 31 Doubly transitive 250 Dual diagram 323 Dyadic rationals 331 EDGE 367 Eilenberg, S. 358 Eilenberg- Moore 54 Elementary abelian p-group 42 Elementary divisors, abelian group 132 Elementary divisors, matrix 141 Elementary moves on path 369 Elementary operation in semigroup 426 Elementary transvection 220 Empty word 344 End path 368 End path class 368 Endomorphism 144 Endomorphism, ring 334 Engel theorem 115 Enumerates 422 Equivalence, characteristics 332 Equivalence, class 477 Erlangen program 72 Euclid's lemma 490 Euler 27 Euler — Poincare characteristic 384 Evaluation map 341 Even permutation 8 Exact sequence 307 Exact sequence, short 307 EXPONENT 26 Exponent, minimal 202 Ext(Q, K) 186 Extension 154 Extension, central 201 Extensions 183 Extensions, forms 238 Extensions, G-invariant 257 Extensions, normal series 99 Extensions, relation 477 Extra-special group 124 Factor group = quotient group 32 Factor group = quotient group, normal series 97 Factor set 180 Faithful G-set 248 Feit — Thompson theorem 107 Fermat theorem 26 Feynmann, R.P. 84 Fiber 380 Field 93 Finite field GF(q) 28 Finite module 135 Finite order, module 135 Finitely generated group 314 Finitely generated group module 135 Finitely presented 400
Реклама
 |
|
О проекте
|
|
О проекте



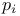 -reduced word
-reduced word  -composition series
-composition series  -subgroup
-subgroup 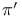 -subgroup
-subgroup  -congruent
-congruent 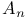
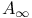

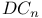
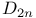
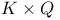
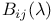
 -function
-function