Авторизация
Поиск по указателям
Rotman J.J. — An Introduction to the Theory of Groups
Обсудите книгу на научном форуме Нашли опечатку?
Название: An Introduction to the Theory of GroupsАвтор: Rotman J.J. Аннотация: Anyone who has studied abstract algebra and linear algebra as an undergraduate can understand this book. This edition has been completely revised and reorganized, without however losing any of the clarity of presentation that was the hallmark of the previous editions.The first six chapters provide ample material for a first course: beginning with the basic properties of groups and homomorphisms, topics covered include Lagrange's theorem, the Noether isomorphism theorems, symmetric groups, G-sets, the Sylow theorems, finite Abelian groups, the Krull-Schmidt theorem, solvable and nilpotent groups, and the Jordan-Holder theorem.The middle portion of the book uses the Jordan-Holder theorem to organize the discussion of extensions (automorphism groups, semidirect products, the Schur-Zassenhaus lemma, Schur multipliers) and simple groups (simplicity of projective unimodular groups and, after a return to G-sets, a construction of the sporadic Mathieu groups).
Язык: Рубрика: Математика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 1995Количество страниц: 513Добавлена в каталог: 09.12.2006Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Finitely related = finitely presented 400 First cohomology group 212 First isomorphism theorem 35 Fitting subgroup 118 Fitting's lemma, groups 147 Fitting's lemma, Q-groups 153 Fixed element of G-set 248 fixes 3 Four group = 4-group V 15 Frattini argument 81 Frattini subgroup 122 Frattini theorem 123 Free Abelian group 312 Free group 343 Free product 388 Free product with amalgamated subgroup = amalgam 401 Free semigroup 349 Freely reduced word 434 Freiheitsatz 449 Fridman, A.A. 450 Frobenius complement 254 Frobenius group 254 Frobenius kernel 252 Frobenius, G. 58 132 199 Fuchs, L. 334 Full subcomplex 367 Fully invariant subgroup 108 Function 479 Functor, contravariant 336 Functor, covariant 335 Functor, left exact 336 Fundamental group 370 Fundamental Theorem Arithmetic 101 490 Fundamental Theorem Combinatorial Group Theory 436 Fundamental Theorem Finite Abelian Groups 132 Fundamental Theorem Finitely Generated Abelian Groups 319 Fundamental Theorem Finitely Generated Modules 142 Fundamental Theorem Projective Geometry 277 G-invariant equivalence relation 257 G-isomorphism 260 G-map 260 G-set 55 G-set, block 256 G-set, doubly transitive 250 G-set, faithful 248 G-set, imprimitive 256 G-set, isomorphism 282 G-set, k-transitive 250 G-set, multiply transitive 250 G-set, primitive 256 G-set, rank 249 G-set, regular 252 G-set, right 55 G-set, sharply k-transitive 251 G-set, trivial 248 Galois field GF(q) 218 Galois group 93 Galois theorem 96 Galois, E. 1 493 Gaschiitz theorem 191 Gaschiitz, W. 123 GCD 487 General linear group GL(n, k) 13 219 Generalized associativity 11 Generalized quaternions 87 Generates 22 Generators and relations, abelian groups 314 Generators and relations, groups 345 Godel image of presentation 465 Godel number 423 Graph 174 Graph, directed 356 Green, l.A. 366 Group 12 Group of motions 64 Group of units 13 Group, 284 Group, 288 Group, 289 Group, 290 Group, 291 Group, 292 Group, abelian 13 Group, affine Aff(n, k) 264 Group, affme group of the plane 71 Group, alternating 23 Group, automorphism group 156 Group, balanced 365 Group, binary tetrahedral 350 Group, braid 347 Group, characteristically simple 106 Group, circle 18 Group, classical 239 Group, complete 158 Group, cyclic 21 Group, dicyclic 351 Group, dihedral D 2n 68 Group, divisible 320 Group, elementary abelian p- 42 Group, extra-special 124 Group, finitely generated 314 Group, finitely related 400 Group, four group = 4-group V 15 Group, free 343 Group, free abelian 312 Group, fundamental 370 Group, Galois 93 Group, general linear GL(n, k) 13 Group, generalized quaternions 87 Group, hamiltonian 87 Group, holomorph 164 Group, icosahedral 69 Group, indecomposable 145 Group, infinite alternating 51 Group, infinite dihedral 391 Group, integers mod 13 Group, modular 391 Group, nilpotent 115 Group, octahedral 69 Group, operator 151 Group, orthogonal 64 Group, orthogonal O(n, k) 239 Group, p-group 73 Group, p-primary 126 Group, perfect 263 358 Group, periodic 155 Group, projective unimodular PSL(n, k) 223 Group, quaternions Q 83 Group, quotient 32 Group, reduced abelian 322 Group, rotation 65 Group, simple 39 Group, solvable 97 Group, special linear SL(n, k) 23 Group, supersolvable 107 Group, symmetric 12 Group, symmetry group of figure 67 Group, symplectic Sp(2m, k) 238 Group, T (order 12) 84 Group, tetrahedral 69 Group, torsion 308 Group, torsion-free 155 308 Group, unitary U(n, k) 238 Group, unitriangular UT(n, k) 82 Groupoid 370 Gruen, O. 199 Gruenberg lemma 214 Gruenberg — Wehrfritz 215 Grushko theorem 393 h-special word 427 Hall subgroup 110 Hall theorem 108 110 Hall — Higman theorem 136 Hall, M. 387 Hall, P. 25 116 166 Hamilton, W.R. 69 Hamiltonian group 87 Height 332 Height, sequence 332 Hermitian form 235 Higher centers , 113 Higher commutator subgroups 104 Higman theorem 451 Higman, G. 86 136 407 Higman, Neumann, and Neumann theorem 404 405 Hirshon R. 150 HNN extension 407 411 Hoelder theorem 160 197 Hoelder, O. 101 154 Holomorph 164 Homogeneous coordinates 273 Homomorphism 16 Homomorphism, crossed 211 Homotopic 369 Hopf's formula 358 Humphreys, J.E. 391 Hyperbolic plane 240 Hyperplane 66 228 Icosahedral group 69 Idempotent endomorphism 144 Identity element 14 Identity function 480 Image = im 22 Imbedding 23 Imbedding free product 388 Imprimitive G-set 256 Imprimitive system 257 Inclusion function 480 Indecomposable group 145 Independence in abelian group 127 310 INDEX 25 Infinite alternating group 51 Infinite dihedral group 391 Injection 480 Injective property 320 Inner automorphism 156 Inner automorphism group Inn(G) 156 Inner product, matrix 235 Inner product, space 235 Instantaneous description 421 Instantaneous description, terminal 422 Integers mod 13 Intersection of subcomplexes 368 Invariant factors, abelian group 129 Invariant factors, matrix 139 Invariant subspace 135 Inverse element 14 Inverse function 480 Inverse image of subcomplex 377 Inverse word 344 Involution 68 Involves 413 Isometry 237 Isomorphism, complexes 371 Isomorphism, field 93 Isomorphism, G-sets 282 Isomorphism, groups 16 Ivanov, S. 136 Iwasawa criterion 263 Jacobi identity 118 James, R. 86 Johnson, D.L. 350 Jonsson, R 334 Jordan — Dickson theorem 232 Jordan — Hoelder theorem, 152 Jordan — Hoelder theorem, groups 100 Jordan — Moore theorem 225 Jordan, C. 101 286 289 Jordan, C., block 139 Jordan, C., canonical form 141 Jordan, C., decompositions 144 Juxtaposition 344 k-transitive 250 Kaloujnine, L. 176 187 Kaplansky, I. 19 330 Kernel, derivation 213 Kernel, group homomorphism 22 Kernel, ring homomorphism 485 Kernel, semigroup homomorphism 350 Klein, F. 72 Kostrikin, A.L. 136 Kronecker, L. 128 Kronecker, L., delta 498 Krull — Schmidt theorem, 153 Krull — Schmidt theorem, groups 149 Kulikov theorem 327 Kulikov, L.J. 330 Kurosh theorem 392 Kuznetsov, A.V. 466 Labeled directed polygon 433 Lagrange's theorem 26 Lagrange, J.-L. 1 57 Lam — Leep 162 285 Lam, C. 294 Landau, E. 77 Latin square 18 Least criminal 111 Left exact functor 336 Length, cycle 3 Length, normal series 97 Length, path 368 Length, word 418 Levi, F. 383 Lifting extension 178 Lifting path 378 Linear fractional transformation 281 Linear functional 229 Lodovici Ferrari 90 Lower central series 113 Lyndon, R.C. 433 Mac Lane, S. 358 Magnus, W. 449 Mann, A. 74 Mann, H.B. 31 Markov property 468 Markov — Post Theorem 428 Mathieu groups, 284 Mathieu groups, 288 Mathieu groups, 289 Mathieu groups, 290 Mathieu groups, 291 Mathieu groups, 292 Matrix of linear transformation, relative to ordered basis 137 Maximal divisible subgroup 321 Maximal normal subgroup 39 Maximal tree 373 McCormick, G. 200 McIver, A. 86 McKay, J.H. 74. McLain, D.H. 115 176 Miller, C.F., III 430 467 Miller, G.A. 292 Minimal exponent 202 Minimal generating set 124 Minimal normal subgroup 105 Minimum polynomial 139 Modular group 391 Modular law 37 Module 134 Monomial matrix 46 177
Реклама
 |
|
О проекте
|
|
О проекте



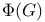
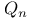

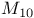

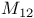
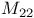
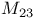
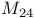
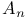
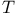
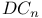
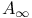
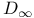

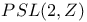

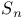

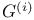

 -groups
-groups