|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Stein E.M. Ч Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscilattory Integrals |
|
|
 |
| ѕредметный указатель |
Pseudo-differential operators, adjoints 233
Pseudo-differential operators, multiplication 231 549
Pseudo-differential operators, multiplier 231 549
Pseudo-differential operators, nonlocal 267Ч268 (see also УSymbols
Pseudo-locality 236 323 396 402
Pseudoconvexity 593Ч594
Qeal-variable structures 4 8Ч9 37Ч41 619
Quantization 548Ч549
Quasi-conformal mappings 41
Quasi-conformal mappings and BMO 180 219
Quasi-distance 10 41 473 478 542
Rademacher functions 457 464
Rectangles see УAverages over rectanglesФ
Rectangles, dual 419
Rectangles, orientation 445
Rectangles, reach 435 445 453
Restricted boundedness 293Ч297 301 307 310 323Ч326
Restriction theorems 352Ч355 364Ч368 386Ч388
Restriction theorems and Bochner Ч Riesz means 422
Restriction theorems and differential equations 368Ч372
Restriction theorems in 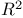 412Ч414 418 412Ч414 418
Restriction theorems in  , n > 3 423 , n > 3 423
Restriction theorems on  642 642
Restriction theorems on compact manifolds 431
Restriction theorems, curved hypersurfaces 365 386Ч388
Restriction theorems, finite type 352Ч353 418
Restriction theorems, method of 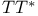 353 364 353 364
Restriction theorems, sharp exponents 352 365 367 387Ч388 414 418 430
Restriction theorems, sphere 365 430
Restriction theorems, unbounded varieties 365Ч368
Reverse Holder inequalities 177 201Ч203 212Ч214 218Ч220 224 225
Riemann singularity 277Ч278 339Ч341 357
Riesz product 40
Riesz representation theorem 143
Riesz transforms 26 317
Riesz transforms and  121 123Ч124 134 138 121 123Ч124 134 138
Riesz transforms and BMO 179
Riesz transforms, analogues for  605Ч608 605Ч608
Scaled family 496
Schrodinger equation 369 522
Schwartz kernel theorem 261
SchwarzТs inequality 499
Seminorms  89 94 99 294 89 94 99 294
Sharp function 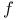 146Ч147 146Ч147
Sharp function 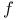 and singular integrals 157Ч158 and singular integrals 157Ч158
Sharp function 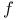 , ,  148Ч149 148Ч149
Sharp function 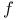 , dyadic , dyadic  151 153Ч155 151 153Ч155
Singular integrals 3 7Ч8 16Ч36 241Ч249 289Ч316
Singular integrals and  235 241Ч249 235 241Ч249
Singular integrals and 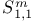 269 302 324 269 302 324
Singular integrals and BMO 300Ч305 325
Singular integrals and sharp function 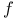 157Ч158 157Ч158
Singular integrals and weights 204Ч211 221
Singular integrals on 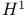 113Ч114 138 178 292 402Ч403 113Ч114 138 178 292 402Ч403
Singular integrals on  557Ч568 580Ч581 586 557Ч568 580Ч581 586
Singular integrals on  22 115Ч118 22 115Ч118
Singular integrals on  20Ч22 42 20Ч22 42
Singular integrals on  24Ч30 248Ч249 289Ч317 323Ч326 562Ч567 623Ч627 24Ч30 248Ч249 289Ч317 323Ч326 562Ч567 623Ч627
Singular integrals on  18Ч23 567Ч568 623 627 18Ч23 567Ч568 623 627
Singular integrals on 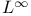 42 155Ч157 178 300Ч305 310 42 155Ч157 178 300Ч305 310
Singular integrals on BMO 157 179
Singular integrals on homogeneous groups 622Ч627
Singular integrals, adjoints 36 156 294
Singular integrals, bounds independence of dimension 523Ч525 (see also УCancellation conditionsФ)
Singular integrals, characterize BMO 179 184
Singular integrals, classical 44
Singular integrals, dyadic decomposition 246Ч247 295Ч296
Singular integrals, kernels 18Ч19 24Ч30 45 245Ч249 289Ч293 296 305Ч308
Singular integrals, multipliers 245Ч249 262Ч263
Singular integrals, nondegenerate 210
| Singular integrals, product theory 85
Singular integrals, rough kernels 372Ч373
Singular integrals, sharp bounds 42
Singular integrals, truncation 30Ч36 80 204Ч210 222 306Ч308
Singular integrals, vector-valued 28Ч29 46Ч48 74 76
Singular Radon transforms 513Ч517 581 641
Sp(n,R) 577Ч579
Square functions 26Ч29 158Ч173 180Ч184
Square functions and  172 172
Square functions and 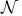 161Ч164 180Ч184 161Ч164 180Ч184
Square functions and averaging operators 487
Square functions and BMO 158Ч173 180Ч184
Square functions and Bochner Ч Riesz means 421
Square functions and dyadic decomposition 267 (see also Уg-functionФ)
Square functions and maximal averages 462Ч463 465 470Ч471 474Ч476 478 480
Square functions and singular integrals 26Ч29 164
Square functions,  161Ч164 161Ч164
Square functions, discrete 161
Square functions, martingale 187
Square functions, nondegenerate 46Ч47 158Ч159 170 186
Square functions, nontangential  27 27
Square functions, vertical  27 326 27 326
Stationary phase 329 334 344 358
Steepest descent 374
Stopping time 162 179 317
Strong convergence 318
SU(n + l,l) 574
Subharmonicity 122Ч123 133
Submanifolds, definition of integral 498
Symbolic calculus 268
symbols 228 231 261
Symbols, asymptotic expansion 265Ч266
Symbols, compound 258Ч260 553
Symbols, order 232
Symplectic invariance 551 577Ч579
T(b) theorem 316 (see also УCauchy integralФ)
T(l) theorem 293Ч305 310 325
Tent spaces see У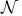 Ф Ф
Tents T(B) 58Ч61 64 80 125
Trace-class space 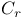 48 48
Tube domains 82 132 447Ч449 458Ч459
Twisted convolution 5 552Ч553 556Ч566 581
Unconditional bases 191
V(x,y) see УVolumeФ
Vector fields 11 38Ч39
Vector fields, bracket 544 (see also УCommutation relationsФ)
Vector fields, exponential mapping 516 584
Vector fields, finite-type condition 38Ч39 516
Vector fields, left-invariant 544
Vector-valued inequalities 47 51 450Ч452
Vector-valued inequalities and weights 222
Vector-valued inequalities on  419 419
Vector-valued inequalities, maximal functions 50Ч56 75Ч76 80 463
Vector-valued inequalities, singular integrals 28Ч29 46Ч48 74 76
VMO (vanishing mean oscillation) 180 224
Volume 8Ч9 29Ч30 42 542
Walsh basis 188
Wave equation 174 368Ч372 395 425 518Ч519
Wave equation in 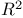 519Ч523 519Ч523
Wavelets 173 189Ч191
Weak boundedness 310 325
Weak-type (1,1) 20
Weak-type (1,1) and  113 137 113 137
Weak-type (1,1) and orthogonality 431
Weak-type maximal principle 441Ч444 456Ч458
Weighted inequalities 53Ч56 76 220Ч222 226
Weighted inequalities, equal weights see У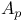 Ф Ф
Weyl correspondence Op(a) 549Ч551 553Ч556 577Ч579
WienerТs principle 93
YoungТs inequality 358
Zygmund condition 225
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте



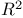
 , n > 3
, n > 3
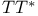


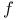



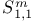
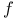
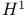



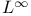
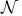



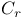
 Ф
Ф