|
|
 |
| јвторизаци€ |
|
|
 |
| ѕоиск по указател€м |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Stein E.M. Ч Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscilattory Integrals |
|
|
 |
| ѕредметный указатель |
Commutators 179
Commutators, Calderon 308Ч312 324
Compensated compactness 137
cones 58 132 447Ч449 461
Cones and spheres 459
Cones, aperture 58 62 93 124Ч127 183Ч184
Conjugate functions and  120Ч123 133 120Ч123 133
Continuity in measure 456Ч458
CotlarТs lemma 279Ч282 318
CotlarТs lemma for integrals 318
Covering lemmas 4 84 465
Covering lemmas, Besicovitch 44
Covering lemmas, Borel Ч Cantelli 442Ч443
Covering lemmas, Vitali 8 12 84
Covering lemmas, Whitney decomposition 14Ч17 60 76 102 206
Critical points 334 341
Critical points, absence 331 341
Critical points, degeneracy 344
Critical points, degenerate 332 334 342
Critical points, nondegenerate 344 380
Curvature 5
Curvature and averages 467Ч469
Curvature and Fourier transforms 330
Curvature, cinematic 519Ч520 (see also УFinite typeФ)
Curvature, Gaussian 348 351 360Ч363 494Ч497
Curvature, principal 348 351 360Ч361 365
Curvature, rotational 494Ч497 500 517
Curvature, total 348
Differentiation of integrals 13 44 65 433 441 455
Differentiation of integrals over hypersurfaces 469 509
Differentiation of integrals over submanifolds 492Ч493
Dilations (non-isotropic) 10 37 45 186 277 473 478 486 514 530 541 618
Dini modulus 29 34 72 80 83 481
Dirichlet problem 24 223Ч225 590 629
Dirichlet problem for 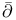 641Ч642 641Ч642
Distance see УQuasi-distanceФ
Distributional inequalities 23 69 151Ч155 184 188 206Ч209
Doubling measures 8 12 39Ч41 151 196 218
Doubling measures and Zygmund condition 225
Duality, 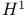 and BMO 142Ч144 163Ч165 178 183 and BMO 142Ч144 163Ч165 178 183
Duality,  and and 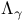 130 130
Duality, 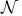 and and 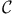 59Ч61 63 77 161Ч163 59Ч61 63 77 161Ч163
Duality,  and and 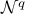 181 181
Duality, inequalities 59 146Ч147 161Ч163
Duality, VMO and 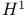 180 180
Dyadic cubes 149
Dyadic decomposition 241Ч243 253Ч257 403
Dyadic decomposition and square functions 267
Dyadic decomposition for  243Ч245 253Ч257 243Ч245 253Ч257
Dyadic decomposition for 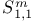 271Ч275 271Ч275
Dyadic decomposition for singular integrals 246Ч247 295Ч296
Dyadic decomposition in 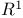 501 506 501 506
Dyadic decomposition, nondyadic decompositions 282Ч285 319
Dyadic decomposition, second 403Ч406 419 522Ч523
Eikonal equation 425
Elliptic operators 230Ч231 241 266
Elliptic operators and weights 223Ч225
entropy 83
Euclidean balls 9
Euclidean measure 9
Exponential integrability 144Ч146 154Ч155 184
Exponential sums 373
Fatou theorem 119Ч120 133
Finite type 350Ч351
Finite type and vector fields 516
Fourier integral operators 173 375Ч376 394Ч412 424Ч429
Fourier integral operators and 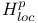 136 429 136 429
Fourier integral operators and averages over hypersurfaces 360 496 517
Fourier integral operators and fractional integration 399Ч401 428Ч429
Fourier integral operators and pseudo-differential operators 395 402Ч403
Fourier integral operators in 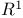 430 430
Fourier integral operators in 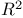 519Ч523 519Ч523
Fourier integral operators on 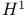 402Ч405 410Ч411 428 402Ч405 410Ч411 428
Fourier integral operators on  397Ч398 397Ч398
Fourier integral operators on  399 402 410Ч412 399 402 410Ч412
Fourier integral operators on 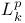 429 429
Fourier integral operators on 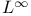 411 (see also УPhase functionsФ) 411 (see also УPhase functionsФ)
Fourier integral operators on 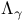 429 429
Fourier integral operators, adjoints 400 410
Fourier integral operators, examples 394Ч396
Fourier integral operators, extended 424Ч425
Fourier integral operators, frequency decomposition 403Ч410
Fourier integral operators, kernels 396
Fourier integral operators, kernels in BMO 427
Fourier integral operators, sharp exponents 426 428
Fourier integral operators, singular set  396 403 396 403
Fourier transform 3 228 557
Fourier transform and oscillatory integrals 378
Fourier transform of surface-carried measure and  360 360
Fourier transform of surface-carried measure and singular integrals 372Ч373
Fourier transform of surface-carried measure, sphere 174 347Ч348
Fourier transform of surface-carried measure, unbounded 363Ч364
Fourier transform of surface-carried measures 347Ч351 360Ч364
Fourier transform of surface-carried measures and averages over hypersurfaces 468
Fourier transform of surface-carried measures and averages over submanifolds 468
Fourier transform of surface-carried measures and number theory 362Ч363
Fourier transform of surface-carried measures and principal curvatures 360Ч361 365
Fourier transform of surface-carried measures and real-variable structures 361 (see also УRestriction theoremsФ)
Fourier transform of surface-carried measures, curvature has zeros 360Ч362
Fourier transform of surface-carried measures, curved hypersurfaces 348Ч350 360
Fourier transform of surface-carried measures, finite type 350Ч351 353 475 479 492
Fourier transform of surface-carried measures, homogeneous 363Ч364
Fourier transform of surface-carried measures, hyperplanes 351
Fourier transform of surface-carried measures, measure in  372Ч373 372Ч373
Fourier transform of surface-carried measures, real analytic 361
Fourier transform on  569Ч573 569Ч573
Fourier transform, convergence 388Ч390 423
Fourier transform, measures of bounded variation 420 (see also УMultipliersФ)
Fourier transform, nondyadic decompositions 282Ч285 319
Fourier transform, radial functions 430
Fractional integration 353Ч354 414
Fractional integration and  136 136
Fractional integration and BMO 178
Fractional integration and Fourier integral operators 399Ч401 428Ч429
Fractional integration and real-variable structures 45
Fractional integration on 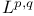 265 265
Fractional integration, imaginary order 33 46
Freeing of monomials see УLifting techniqueФ
Freezing principle 230Ч231
Functional calculus 231
G-function 47 524
Garding inequalities 321
Gaussian kernel 24
Global  -density 62 126 -density 62 126
H-type groups 636
Haar basis 173 190
Haar basis, generalized 312Ч316
Hardy Ч Littlewood Ч Sobolev theorem see УFractional integrationФ
Harmonic measure 41 224Ч225
Hausdorff Ч Young inequality 583
Heat equation 24 276
Heat equation on  632Ч633 642Ч643 632Ч633 642Ч643
Helson Ч Szego theorem 225Ч227
Hermite expansions 571Ч573 582Ч584
Hermite operator 549 571 579 598
Hessian determinant 377 384
Hessian determinant and rotational curvature 496
Hessian determinant, zeros 412 415
Hilbert transform 3 26 225Ч227 389 424
Hilbert transform and Cauchy integral 311
Hilbert Ч Schmidt class 554Ч556 570Ч571
Hilbert Ч Schmidt norm 415
Homogeneous dimension 478 620 638
Homogeneous distributions 45 262Ч263
Homogeneous groups 11 83 186 618Ч627 635Ч641
Homogeneous groups, balls  620 620
Homogeneous groups, dilations 618 621 637
Homogeneous groups, examples 620Ч621
Homogeneous groups, Haar measure 619
Homogeneous groups, Lie algebras 621Ч622 635Ч637
| Homogeneous groups, lifting technique 639Ч641
Homogeneous groups, maximal functions 638
Homogeneous groups, nilpotence 621
Homogeneous groups, norm  619 638 619 638
Homogeneous groups, singular integrals 622Ч627
Hyperbolic equations 372 395 425 428 429
Hypoellipticity 39 604
Infinite constant 304
Interpolation of operators and  137 185 137 185
Interpolation of operators and 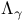 255 255
Interpolation of operators and 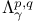 264 264
Interpolation of operators and BMO 173Ч177
Interpolation of operators, averaging operators 371
Interpolation of operators, complex  384Ч385 384Ч385
Interpolation of operators, Fourier integral operators 410Ч412
Interpolation of operators, Fourier restriction 352 365
Interpolation of operators, Marcinkiewicz 14 22 36 265 465
Interpolation of operators, maximal averages 14 479Ч482 487Ч489 503 507 518Ч519
Interpolation of operators, oscillatory integrals 381Ч386
Interpolation of operators, singular integrals 22 36 514
Iwasawa decomposition 621 637
John Ч Nirenberg inequality 144Ч146 154Ч155 179
Jump theorem 580
Kakeya needle problem 434 454Ч455
Klein Ч Gordon equation 372
Kohn Laplacian 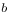 592Ч593 596Ч597 592Ч593 596Ч597
Kohn Laplacian 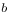 on functions 615Ч618 on functions 615Ч618
Kohn Laplacian 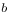 on pseudoconvex domains 639 on pseudoconvex domains 639
Lagrangian distributions 429
Laguerre functions 584
Laplace Ч Beltrami operator 431
Laplacian  24 590 592 629 24 590 592 629
Lattice points, distribution 362
Layer potentials 224
Levi form 593
Lewy operator 611Ч618
Lewy operator, unsolvable equations 612Ч615
Lifting technique 468 513Ч517
Lifting technique and homogeneous groups 639Ч641
Lifting technique, freeing of monomials 477Ч478
Lifting technique, method of descent 483Ч486 490Ч491
Lifting technique, universal variety 477Ч478
Lipschitz domains 137 223Ч225 310Ч316
Littlewood Ч Paley decomposition see УDyadic decompositionФ
LlogL see УOrlicz spacesФ
Local smoothing 521Ч523
Local solvability 604 611
Marcinkiewicz integral 76
Martingales 151 187Ч190
Martingales and real-variable structures 189
Martingales, dyadic 187
Maximal functions 3 7Ч14 49Ч75 87Ч101 433Ч434 440Ч449 455Ч511
Maximal functions and balls  65Ч69 78Ч79 65Ч69 78Ч79
Maximal functions and sets 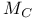 433 441 433 441
Maximal functions and singular integrals 34Ч36 157Ч158
Maximal functions and weights 195 198Ч203
Maximal functions on  87Ч112 87Ч112
Maximal functions on  13Ч14 43 51Ч53 72 84 446 458 13Ч14 43 51Ч53 72 84 446 458
Maximal functions on  317Ч318 317Ч318
Maximal functions on  441 445 441 445
Maximal functions on BMO 179
Maximal functions on homogeneous groups 638
Maximal functions, ![$M_r(f) = [M(|f|^r]^{1/r}$](/math_tex/610ec62944a220a6629e31abd086f87482.gif) 34 157Ч158 219 222 422 34 157Ч158 219 222 422
Maximal functions, bounds independence of dimension 523Ч525
Maximal functions, comparison of 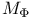 , , 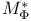 , , 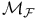 92Ч101\ 92Ч101\
Maximal functions, comparison of M, 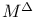 188 188
Maximal functions, dyadic 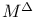 149Ч151 153Ч155 202Ч203 213 149Ч151 153Ч155 202Ч203 213
Maximal functions, grand  90 99Ч100 146 90 99Ч100 146
Maximal functions, homogeneous  72 83 72 83
Maximal functions, linearization 29 49 317Ч318
Maximal functions, martingale 187 223
Maximal functions, nontangential 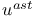 , ,  56Ч57 62 90 92 184 56Ч57 62 90 92 184
Maximal functions, sharp bounds 42
Maximal functions, spherical averages of 466
Maximal functions, strong Ms 83Ч85 446Ч447 458 462
Maximal functions, tangential 79 92
Maximal functions, usual M 3 9 16 354 474 478
Maximal functions, vector-valued 50Ч56 75Ч76 80 463
Maximal functions, vertical 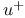 , , 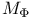 69Ч70 90 69Ч70 90
Maximal functions, weak-type principle 441Ч444 456Ч458
Mehler kernel 582 583
Metaplectic representation 578
Method of descent see УLifting techniqueФ
Method of rotations 72
Molecules 130
Moment conditions 87 99 104Ч106 128 129
MorseТs Lemma 346
Multilinear operators 326Ч328
Multipliers and linear subspaces 515
Multipliers ball 389 450Ч454
Multipliers for singular integrals 24Ч26 245Ч249 262Ч263
Multipliers on  642 642
Multipliers, half-line 452
Multipliers, half-space 450
Multipliers, Marcinkiewicz 26 174 263 464
Nikodym set 455
Nilpotent groups 517 635
Nilpotent groups, free 637 640Ч641
Nilpotent groups, Lie algebras 621 635
Nonmeasurable sets 70 77
One-parameter groups 584
One-parameter groups and dilations 637
Orlicz spaces 43 84 128 458 526
Ornstein Ч Uhlenbeck process 582 642
Orthogonality 278Ч288
Orthogonality and BMO 166Ч173
Orthogonality and singular integrals 295Ч300
Orthogonality on homogeneous groups 623Ч627
Orthogonality, almost 257 269Ч270 278
Orthogonality, lack of 272Ч273
Orthogonality, method of 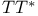 278Ч279 317Ч318 353 364 378 381 398 400 431 278Ч279 317Ч318 353 364 378 381 398 400 431
Oscillatory integrals 3 5 329Ч347 375Ч386 414Ч418
Oscillatory integrals and  581 581
Oscillatory integrals and Fourier transform 378
Oscillatory integrals in 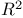 412Ч414 412Ч414
Oscillatory integrals on  377Ч383 500Ч501 377Ч383 500Ч501
Oscillatory integrals on  379Ч386 392Ч393 412Ч414 379Ч386 392Ч393 412Ч414
Oscillatory integrals, adjoints 378Ч381
Oscillatory integrals, asymptotics 334Ч341 355Ч360
Oscillatory integrals, endpoint contributions 331 355
Oscillatory integrals, finite-type phase 416
Oscillatory integrals, localization 330 341 396
Oscillatory integrals, scaling 332 342
Oscillatory integrals, sharp exponents 412 417Ч418
Oscillatory integrals, singular phase 415
Oscillatory singular integrals 373 416Ч417 423 557Ч561
Oscillatory singular integrals on  431 431
Parametrix 241 266
Paraproducts 274 302Ч305 326Ч328
Phase functions 330 377 380 427
Phase functions and Gaussian curvature 360 (see also УHessian determinantФ)
Phase functions and rotational curvature 517
Phase functions, duality 358
Phase functions, extension 381
Phase functions, Newton diagram 359
Phase functions, nondegeneracy 394
Phase functions, oscillatory index 359
Phase functions, polynomial 416
Phase functions, rank 363
Poisson integrals and BMO 165
Poisson integrals on  3 90 3 90
Poisson integrals on symmetric spaces 71 78 82 85 447Ч449 458Ч459 637 638
Poisson kernel 24 47 89 99
Poisson kernel for  629 629
Poisson kernel, conjugate 121
Poisson summation formula 362
Principal type 321
Product theory of  83Ч85 138 446Ч447 83Ч85 138 446Ч447
Pseudo-differential operators 5 228Ч288
Pseudo-differential operators and Fourier integral operators 395 402Ч403
|
|
 |
| –еклама |
 |
|
|
 |
|
ќ проекте
|
|
ќ проекте




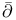
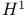 and BMO
and BMO 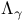
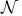 and
and 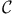
 and
and 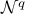

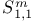
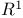
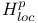
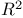


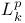
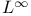



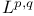
 -density
-density 

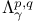
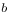


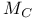

![$M_r(f) = [M(|f|^r]^{1/r}$](/math_tex/610ec62944a220a6629e31abd086f87482.gif)
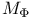 ,
, 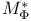 ,
, 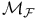
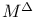

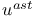 ,
, 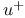 ,
,