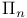|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Stanley R.P. — Enumerative Combinatorics: Volume 1 |
|
|
 |
| Предметный указатель |
Polynomials of degree n, coefficients as finite differences (proposition) 38
Polynomials, bases for 208
Polyominos, definition 256
Polyominos, enumerating horizontally convex 257
Polytope, cyclic 199
Polytope, integral 238
Polytope, rational 235
Poset and  -chain condition 220 -chain condition 220
Poset, basic concents 96
Poset, defining axioms 97
Poset, definition of isomorphic 98
Poset, extension of to total order 110
Poset, Gaussian 270
Poset, locally finite 98
Poset, table of examples 105
Power series, composition defined 6
Power series, rational of one variable 202
Prefabs, literature references 151
Preferential arrangement, definition 146
Preposet 153
Principle of Inclusion-Exclusion and binomial posets 145
Principle of Inclusion-Exclusion and maximal chains in rank-selected sub-poset 131
Principle of Inclusion-Exclusion and Moebius inversion on boolean algebra 118
Prins G. and direct products of posets 175
Probleme des menages and non-attacking rooks 73
Probleme des menages, lemma 73
Proctor R. and Gaussian posets 288
Proctor R. and zeta polynomial 179
Product of convergent formal power series (proposition) 6
Product of words 247
Product theorem and Moebius function 118
Provan J.S. and chain-partitionable posets 193
Pseudo-polynomial or quasi-polynomial 210
q-analogue for number of permutations with descent set S 70
q-binomial coefficient 26
q-binomial coefficient and partitions (proposition) 29
q-Dyson conjecture 54 95
q-multinomial coefficient and multisets 26
Quasi-generators 226
Quasi-generators, completely fundamental elements 228
Quasi-ordered set 153
Quasi-period of quasi-polynomial 210
Quasi-polynomial and convex polytope (theorem) 237
Quasi-polynomial and number of P-partitions (theorem) 216
Quasi-polynomial, definition 210
Quasi-polynomial, properties of (proposition) 210
Quotient of poset relative to closure 159
R-labelings, definition 133
R-labelings, literature references 150
r-stemmed V-partition 89
Rank generating function 99
Rank generating function and simplicial posets 135
Rank generating function, definition of 99
Rank of finite poset 99
Rank-selected Moebius invariant and lattice of subspaces of a vector space 132
Rank-selected Moebius invariant and permutations in Jordan — Hoelder set (theorem) 132
Rank-selected Moebius invariant of a poset 131
Rank-selected Moebius invariant, direct combinatorial interpretation 133
Rank-selected subposets, definition 131
Rank-selected subposets, literature references 150
Rational generating function, coefficients at negative integers 206
Rational generating function, definition 202
Rational generating function, exceptional set 204
Rational power series in one variable 202
Read R.C. and dimers 291
Reciprocity theorem for Ehrhart quasi-polynomials 238
Reciprocity theorem for linear homogeneous diophantine equations 230
Reciprocity theorem for order polynomials 194 219
Reciprocity theorem for P-partitions (theorem) 215
Recurrence and master duality theorem for Eulerian posets 138
Recurrence and Stirling number of the second kind 33
Recurrence for computing coefficients of rational function 205
Recurrence for computing coefficients, negative n 207
Recurrence for Moebius function (corollary) 125
Recurrence for number of linear extensions of poset 112
Recurrence for partitions into k parts 28
Recurrence, defining for Moebius function 116
Reduced Euler characteristic and topological significance of Moebius function 121
Reduced Euler characteristic, definition 120
Reduction of a permutation 172
Reduction, simple 172
Refinement of poset 98
Regev A., constant term of product expansion (exercise) 54
Regular local ring, one-dimensional complete 4
Relative volume of integral polytope 239
Remmel J.B., derangement proof (exercise) 92
Restricted direct product, definition and Moebius function of a poset 119
Restriction of maximal chain 168
Rise as element of permutation 24
Rival I. and core of irreducible poset 176
Rival I. and modular lattice 186
Rival I., finite atomic and coatomic lattice 177
Robbins D. and pleasant posets 182
Roberts F.S. and dimension of poset 176
Rook numbers for Ferrers board (theorem) 74
Rook polynomial and factorization method 255
Rook polynomial and k-discordant permutations 74
Rook polynomial and transfer-matrix method 253
Rook polynomial, equality for Ferrers boards 75
Rooks, non-attacking 71
Roos J.-E. and number of words in quotient monoid 277
Rota G.-C. and chromatic polynomial 187
Rota G.-C. and closure relations 183
Rota G.-C. and homology theory for posets 150
Rota G.-C. and valuation of finite distributive lattice 184
Rothschild B.L. and non-isomorphic n-element posets 174
Row-reduced echelon form and partitions of integers 29
Sachs H. and counting rooted forests (exercise) 94
Saks M. and order polynomial 285
Saturated chain 99
Scheid H. and bounds on Moebius function 186
Schroeder E. and posets and lattices 149
Schuetzenberger M.-P. and jeu de taquin 179
Schuetzenberger M.-P. and weak Bruhat order 199
Secant number or Euler number 149
Self-conjugate partition 58
Semi-Eulerian poset 122
Semilattice, meet- and join- 103
Semimodular lattice and R-labcling 135
Semimodular lattice as R-poset 134
Semimodular lattice, Mobius function of 126
Semimodular lattice, seven-element (figure) 104
Sequences and paths, literature reference 151
Series-parallel posets 100
Serre J.-P. and rational generating functions 276
Sets and multisets 13
Shapiro L. and duality theorem for face lattice of an n-cube 198
Shapiro L., finite differences (exercise) 62
Shearer J.B. and Moebius function 188
Shearer J.B. and number of words in quotient monoid 277
Shephard G.C. and cyclic polytopes 199
Shephard G.C. and zonotopes with integer vertices 290
Shift operator, E 36
Shuffle, definition 70
Shuffle, inverse of permutation 70
Sieve equivalence as variation of involution principle 80
Sieve method for determinine cardinality 64
Simplicial complex and Alexander duality theorem 137
Simplicial finite poset 135
Simplicial submonoid 226
Skyrme T.H.R., proof for partition counts (exercise) 59
Smith, B. Babington and tournament (exercise) 94
Solomon L. and Moebius algebra of poset 150
Solomon L. and subgroups of 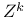 of finite index 190 of finite index 190
Spanning subsets of a vector space, number of 127
Species as alternative to binomial posets, references 151
| Sperner family or antichain 100
Standard permutation 93
Standard representation of permutation 17
Stanley R. and an extremal finite distributive lattice 178
Stanley R. and chain-partitionable Cohen — Macaulay posets 194
Stanley R. and chain-partitionable posets 193
Stanley R. and comparability graph 194
Stanley R. and counting certain permutations 93
Stanley R. and Ehrhart (quasi-)polynomial 290
Stanley R. and finite supersolvable lattice 190
Stanley R. and incidence algebras of locally finite posets 183
Stanley R. and integral convex d-polytopes 288
Stanley R. and order ideals of  277 277
Stanley R. and order polynomial 181
Stanley R. and pleasant posets 182
Stanley R. and toric varieties and hard Lefschetz theorem 198
Stanley R. and trapezoidal chains and antichains 179
Stanley R. and weak Bruhat order 199
Stanley R., convex polytope and Eulerian lattice 199
Stanley R., count of subsets mod n (exercise) 60
Stanley R., cycle types of permutations (exercise) 61
Stanley R., free R-module and supersolvable poset 192
Stanley R., intersection (co)homology 199
Stembridge J. and a zeta polynomial 179
Stembridge J. and trapezoidal chains and antichains 179
Stirling number of the first kind 18
Stirling number of the first kind and calculus of finite differences 36
Stirling number of the first kind and exponential generating function (proposition) 19
Stirling number of the first kind and polynomial generating function 208 209
Stirling number of the first kind and Twelvefold Way 35
Stirling number of the first kind as number of integer sequences (proposition) 20
Stirling number of the first kind, recurrence (lemma) 18
Stirling number of the second kind and characteristic polynomial of 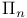 128 128
Stirling number of the second kind and Moebius function of poset 128
Stirling number of the second kind and partitions of a set 33
Stirling number of the second kind and polynomial generating function 208 209
Stirling number of the second kind, exercise 57 47
Stirling numbers, examples of matrices 36
Stonesifer J.R. and uniform geometric lattice 191
Stong R.E. and core of irreducible poset 176
Strauss E.G. and basis for group of polynomials (exercise) 62
Strong fixed point, definition of, for permutation 49
Submonoid of monoid 247
Submonoid, simplicial (lemmas) 226
Subposet of P, S-rank selected 131
Subposet, convex 98
Subposet, induced 98
Subposet, weak 98
Subspaces of vector space, number of (proposition) 28
Sum of convergent formal power series (proposition) 6
Supersolvable finite lattice, additional properties 163—164
Supersolvable finite lattice, definition 134
Supersolvable finite lattice, non-semimodular (figure) 134
Szegoe G. and value of a determinant 184
Tangent number or Euler number 149
Tanny S.M. and counting certain permutations (exercise) 93
Temperley H.N. and counting rooted forests (exercise) 94
Terao H. and arrangements of hyperplanes 192
Terao H., Removal Theorem 192
Terquem's problem (exercise) 63
Thevenaz I., Moebius function of lattice of subgroups 191
Tournament 90
Transfer-matrix method 241
Transition matrix for polynomial bases 35 209
Tree, definition 293
Tree, definition of binary 23
Triangular board and rook number (corollary) 75
Triangular poset 173
Triangulation of pointed convex polyhedral cone 223
Trotter W.T.J. and dimension of poset 176
Twelvefold Way 31—40
Twelvefold Way, table 33
Two tree representations and permutation statistics 23
Underlying space of finite regular cell complex 121
Unfixed points for permutations and dependence on n 68
Uniform poset 165
Unimodal sequence of weight n 76
Unimodal sequence, expression for and V-partition (proposition) 78
Unimodal sequence, number of analogous to partitions of n 76
Unique factorization domain 4
V-partitions and unimodal sequences 76
V-partitions of n, definition 77
V-partitions, definition of r-stemmed 89
V-partitions, number of and sieve-theoretic formula 78
Valley as element of permutation 24
Valuation 160
van der Poorten A.J. and rational generating functions 276
Veress P., combinatorial proof (exercise) 52
Verma D.-N. and Bruhat order 199
Very pure monoids, characterization (propositions) 249
Wachs M. and Bruhat order 199
Walch R., counting triangles with perimeter n 281
Walk in digraph 241
Walk, closed 241 293
Walk, definition 293
Walker J. and topological properties of posets 150
Ward M. and Moebius inversion formula 149
Weak excedance of permutation 23
Weak subposet 98
Weight of multiset cycle, definition 47
Weighted cardinalities 66
Weil A. and Weil conjectures 279
Weil Conjectures 279
Weipht function for set 65
Weipht function on set of edges of digraph 241
Weisner L. and Moebius inversion formula 149
Weisner's theorem (corollary 3.9.3) 125
Well-defined operations (example) 5
Wensley C.D., Moebius function of subgroup lattice of symmetric groups 191
West D. and chains in posets 175
Whitney number of the first kind, coefficient of characteristic polynomial 129
Whitney number of the second kind and Dehn — Sommerville equations (proposition) 136
Whitney number of the second kind and number of elements of rank k 129
Whitworth W.A. and counting certain permutations (exercise) 93
Wilf H. and meet-semilattice 184
Wilson K. and q-Dyson conjecture 54
Wilson R. and permutation of finite lattice 185
Wilson R. and Whitney number inequalities 185
Winkler P. and comparability graph 194
Winston K. and outdegree sequences 290
Wisner R.J., counting triangles with perimeter n 281
Word as finite sequence of letters 247
Word to represent a permutation 16
Worley Dale and a recurrence for partitions (exercise) 59
Yoder M.F., count of subsets mod n (exercise) 60
Young diagram and partitions of n 29 30
Young's lattice 168
Zaslavsky T. and Dowling lattice 191
Zaslavsky T. and hyperplane arrangements 192
Zaslavsky T. and the acyclotope 290
Zeilberger D. and cluster generating function 280
Zeilberger D. and tournament (exercise) 95
Zeilberger D., proof of q-Dyson conjecture 54
Zeta function and zeta polynomials 130
Zeta function, definition 114
Zeta polynomials 129
Zeta polynomials and binomial posets 145
Zeta polynomials and number of chains 129
Zeta polynomials and order polynomial 130
Zeta polynomials, definition 129
Zeta polynomials, literature references 150
Ziegler G. and Moebius function 187
Ziegler G. and self-dual poset 175
Ziegler G. and zigzag posets 181
Ziegler G., partitions of integer ordered by refinement 192
Zonotope 290
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 -chain condition
-chain condition 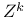 of finite index
of finite index