|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Stanley R.P. — Enumerative Combinatorics: Volume 1 |
|
|
 |
| Предметный указатель |
Generating function, extracting information from 10
Generating function, fundamental for P-partition 212
Generating function, fundamental, and Jordan — Hoelder set (theorem) 214
Generating function, ordinary 141
Generating function, r-exponential 141
Generating function, rational, and adjacency matrices 245
Generating function, reasons for using 3
Generating function, sets associated with 143
Geometric lattice and partition lattice 128
Geometric lattice, definition of 105
Geometric representation of permutations 23
Gessel I.M. and a recurrence relation 282
Gessel I.M. and duality theorem for Eulerian posets 198
Gessel I.M. and formal power series for rational function 275
Gessel I.M. and strong fixed point of permutation (exercise) 61
Gessel I.M. and vector partitions 282
Gessel I.M., tournament (exercise) 94
Gleason A. and direct products of posets 175
Good I.J., proof of Dyson conjecture 54
Gordon B. and pleasant posets 182
Goresky M., intersection (co)homology 199
Gould H.W. and formal power series (exercise) 62
Goulden I.P. and binomial poset 201
Goulden I.P. and cluster generating function 280
Graded posets, definition 99
Graded posets, ranks of (table) 99
Graph, definition for permutation 71
Graph, directed 241
Greene C. and geometric sublattice 178
Greene C. and maximum size antichains 182
Greene C. and meet-distributive meet-semilattice 179
Greene C. and Moebius algebras 150
Greene C. and Moebius functions 149
Greene C. and rank inequality for finite geometric lattice 185
Greene C. and subsets of finite lattice 186
Greene C. and weak Bruhat order 199
Greene C., partitions of integer ordered by dominance 192
Gross O.A., chains in boolean algebra, literature references 151
Guibas L.J. and autocorrelation polynomial 280
Gunson J. and Dyson conjecture 54
Hadamard product and generating function with weighted edge 258
Hadamard product and sums over compositions 258
Hadamard product for rational power series (proposition) 207
Haiman M. and order ideals 182
Hajos G., combinatorial proof (exercise) 52
Hall P. and Moebius inversion formula 149
Hanlon P. and Gaussian poset 287
Harbater David and integral power series 276
Hasse diagram for 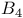 (figure) 108 (figure) 108
Hasse diagram for direct product of two posets (figure) 101
Hasse diagram of finite poset 98
Hasse diagram, edges of and R-labeling 133
Hasse diagram, method for drawing (figures) 109
Hasse diagram, method for drawing, finite order ideals of poset 108
Hasse diagrams of lattices (figures) 102
Hawkins T. and history of group representations 290
Hilton P.J. and duality for abelion groups 190
Hock, J.L. and dimers 291
Horizontally convex polyominos 256
Hurwitz A. and Fatou's lemma 275
Hyperplane arrangement 166
Igusa, J.-L. and congruences mod 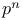 279 279
Incidence algebra and algebra of upper triangular matrices 114
Incidence algebra of a locally finite poset 113
Incidence algebra, subalgebra of and binomial poset (theorem) 144
Incident, edges and vertices 293
Inclusion-Exclusion, dual form 66
Inclusion-Exclusion, Principle of 64
Inclusion-Exclusion, Principle of (theorem) 64
Indecomposable permutation 49
Index, greater (major), of permutation 216
Indik R. and a recurrence relation 282
Indistinguishable, elements of set 31
Inequivalent injective functions, number of, definition 32
Inequivalent sets 31
Integral convex d-polytope and relative volume 239
Interior of simplicial submonoid 226
Inverse of elements of formal power series 4
Inverse of matrix for Stirling number of the second kind 35
Inversion and permutation statistics 20
Inversion table of permutation 21
Inversion, definition of, for multiset permutation 26
Inversion, definition of, for permutation 21
Inversion, number of, for permutations (corollary) 21
Involution principle for converting proofs to combinatorial proofs 80
Involutions 79
Involutions, construction of for intersecting lattice paths 84
Irreducible finite poset 155
Isomorphic posets 98
Jackson D.M. and cluster generating function 280
Jackson D.M. and descents of permutations 201
Jambu M. and intersections of hyperplanes 192
Jeu de taquin 179
Join for elements of poset 102
Join-irreducible of finite distributive lattice (proposition) 106
Join-irreducible, element of lattice 106
Jordan J.H., counting triples 281
Jordan, Charles, number of objects of finite set (exercise) 91
Jordan-Hoelder set and P-partitions (lemma) 213
Jordan-Hoelder set and supersolvable lattices 164
Jordan-Hoelder set, definition of 131
k-composition of n, schematic representation 15
k-composition, definition 14
k-composition, weak 15
k-discordant permutations, problem of 74
Kahn J. and order polynomial 285
Kasteleyn P.W. and dimers 291
Katz N.M. and Weil conjectures 279
Kelly D. and dimension of poset 176
Kelmans A.K. and counting rooted forests (exercise) 94
Kendall M.G. and tournament (exercise) 94
Kim D. and chromatic polynomial 292
Kirdar M.S., proof for partition counts (exercise) 59
Klarner D.A. and dimers 291
Klarner D.A. and rational generating functions 276
Klarner D.A., decomposition of permutations of sets (exercise) 47 57
Kleitman D.J. and free distributive lattice 181
Kleitman D.J. and maximum-size antichains 182
Kleitman D.J. and meet-distributive meet-semilattice 179
Kleitman D.J. and meet-irreducible elements of finite lattice 177
Kleitman D.J. and non-isomorphic n-element posets 174
Kleitman D.J. and order ideals 182
Kleitman D.J. and outdegree sequences 290
Kleitman D.J., combinatorial proofs (exercise) 52
Knuth D.E. and monoid 189
Knuth D.E. and number of words in quotient monoid 277
Knuth D.E., inversion polynomial (exercise) 61
Knuth D.E., multiset permutations 57
Koblitz N. and Well conjectures 279
Koh K.M. and finite distributive lattice 182
Koszul complex 92
Koszul relation 92
Kratzer C., Moebius function of lattice of subgroups 191
Kreweras G. and non-crossing partitions 197
Kreweras G. and Young's lattice 195
Kummer E., binomial coefficients and primes (exercise) 53
Kung J. and subsets of finite lattice 186
L-labeling, literature references 150
Lascoux A. and weak Bruhat order 199
Lattice 102
Lattice and Moebius algebras 124
Lattice path 82
Lattice path and number of words in quotient monoid 277
Lattice path and pleasant posets 182
Lattice path and volume of convex polytopes 290
Lattice path, cycle types of permutations (exercise) 61
Lattice path, diagram 82
Lattice path, enumeration of 44 111
Lattice path, intersecting 82
Lattice, atomic 104
| Lattice, complemented 104
Lattice, complete 103
Lattice, distributive 105
Lattice, finitary distributive and FTFDL (proposition) 107
Lattice, finitary distributive, definition 107
Lattice, finite distributive, fundamental theorem for 106
Lattice, finite geometric 105
Lattice, finite semimodular 104 105
Lattice, free distributive 158
Laurent series and rational generating function 206
Lexicographically shellable posets and CL-labeling 151
Lie algebras, semi-simple 288
Lieb E.H. and dimers 291
Lindstroem B. and meet-semilattice determinant 184
Linear extension of poset 110
Linear ordering of elements of multiset 16
Link in a finite simplicial complex 121
Linked sets, literature references 151
Loop of digraph 241
Lucas E., binomial coefficients and primes (exercise) 53
Lucas number and permutation enumeration 246
Lyndon R.C. and multiset permutations (exercise) 57
Macdonald I.G., constant term of product expansion (exercise) 54
MacMahon P.A. and recurrence formula (exercise) 58
MacMahon P.A. and Young's lattice 195
MacNeille completion of irreducibles of finite lattice 176
MacPherson R., intersection (co)homology 199
Magic squares, number of (proposition) 232
Mani P. and Ehrhart polynomial 288
Markowsky G. and free distributive lattice 181
Maximal chain and supersolvable finite lattice 134
Maximal chains in distributive lattice 110
Maximal chains, number of and R-labeling (theorem) 133
McMullen P. and cyclic polytopes 199
McMullen P. and Ehrhart quasi-polynomial 290
McQuistan R.B. and dimers 291
Meet-distributive, meet-semilattice 156
Meet-semilattice, conditionally a lattice (proposition) 103
Meuser D. and congruences mod 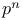 279 279
Milne S., Stirling number of the second kind (exercise) 60
Modular lattice 104
Modular lattice as poset of subspaces of a vector space 127
Moebius algebras, definition for lattice 124
Moebius algebras, theorem 124
Moebius function and count of permutations (lemmas) 147
Moebius function and Eulerian posets (lemmas) 136
Moebius function and Eulerian posets (proportion) 137
Moebius function and finite regular cell complex (proposition) 122
Moebius function and meet of coatoms (corollary) 126
Moebius function for lattice faces of triangulation 224
Moebius function of poset 116
Moebius function of semimodular lattice (proposition) 126
Moebius function, classical 9 119
Moebius function, computing (proposition) 119
Moebius function, determination of, for a boolean algebra 145
Moebius function, function 9
Moebius function, techniques for computing 117
Moebius inversion and Euler characteristic 119
Moebius inversion formula and zeta function 116
Monjardet B. and meet-distributive meet-semilattice 179
Monoid and homogeneous linear equations 221
Monoid, definition 163
Monoid, free, factorization in 247
Monoid, positive 222
Moon J.W. and counting rooted forests (exercise) 94
Moser W.O.J., Terquem's problem (exercise) 63
Multichains and zeta function 115
Multichains and zeta polynomial 130
Multichains of poset 100
Multinomial coefficients q 26
Multinomial coefficients, definition 16
Multiset cycle 47
Multiset permutation 47
Multiset, definition 15
Multiset, generating function approach 15
Multiset, permutations of 16
Multisets, permutations of 25
n-coloring of a graph 162
n-stack 76
Nelson R.B. and volume of a convex polytope 290
Non-crossing partitions 197
Odlyzko A.M. and autocorrelation polynomial 280
Odlyzko A.M., count of subsets mod n (exercise) 60
Open subset of preposet 153
Order by inclusion, poset of subsets 97
Order by refinement, partitions of a set 97 127
Order by refinement, partitions of n 166
Order complex of poset 120
Order ideal, definition of 100
Order ideal, dual 100
Order ideal, principal 100
Order polynomial and  -chain condition (corollary) 221 -chain condition (corollary) 221
Order polynomial and chain length (corollary) 220
Order polynomial, definition 130
Order polynomial, fundamental property (theorem) 219
Order polynomial, reciprocity theorem 194 219
Order polynomial, strict 218
Order-reversing map 211
Order-reversing, strict 211
Ordinary generating function 3
Orientation of edges of finite graph 273
Orientation, acyclic 273
Orlik — Solomon — Terao conjecture 192
Outdegree sequence of orientation 273
P-compatible permutation 171
P-partition and linear homogeneous equations, equivalence of 222
P-partition and strict P-partition (lemma) 220
P-partition, definition 211
P-partition, strict P-partitions and  -chain condition 218 -chain condition 218
Partial G-partition of a set 165
Partial partition of a set 165
Partition and q-binomial coefficient (propositions) 29
Partition of an integer 28
Partition of finite set, definition 33
Partition with restricted parts 38
Partition, definition of self-conjugate 38
Partitions of n-set, definition 33
Partitions of n-set, lattice of 97 127
Partitions of n-set, ordered 34
Pascal's triangle, generalized 112
Peak as element of permutation 24
Peirce C.S. and partially ordered sets and lattices 149
Permutation enumeration and binomial posets 147
Permutation statistics 17
Permutation statistics, cycle structure 17
Permutation statistics, descents 21
Permutation statistics, inversions 20
Permutation with k cycles, and Stirling number 18
Permutations and factorization method 252
Permutations of a multiset 16
Permutations of a multiset and inversions (proposition) 26
Permutations with descent set S, determinant expression for 69
Permutations with restricted position 71
Permutations, alternating and number of complete binary trees 24
Permutations, equivalent 89
Permutations, k-discordant and factorization method 253
Permutations, mapped to inversion table (proposition) 21
Permutations, number, with specified number of maxima (corollary) 20
Permutations, standard 93
Philip Hall's theorem (Proposition 3.8.5) 119
Plane trees and face-lattice of an n-cube 170
Pleasant poset 158
Poguntke W. and comparability graph 194
Point lattice 104
Pollack J. and dimers 291
Polya G. and power series with integer coefficients 282
Polya G. and value of a determinant 184
Polya's enumeration theorem 48
Polynomials 208
Polynomials as coefficients of rational generating functions 208
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



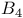 (figure)
(figure) 
 -chain condition (corollary)
-chain condition (corollary)  -chain condition
-chain condition