|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Stanley R.P. — Enumerative Combinatorics: Volume 1 |
|
|
 |
| Предметный указатель |
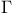 , triangulation of pointed convex polyhedral cone 223 , triangulation of pointed convex polyhedral cone 223
Abelian group 36
Abramson M., Terquem's problem (exercise) 63
Acyclotope 290
Adjacency matrix of digraph 241
Adjacency matrix, entries in 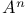 (theorem) 242 (theorem) 242
Aigner M. and closed poset 183
Aigner M. and intervals of posets 175
Aigner M. and uniform geometric lattice 191
Alexander duality theorem for simplical complexes 137
Alexandroff P.S., finite posets and finite topologies 174
Alphabet as finite set 247
Andrews G.E. and pleasant posets 182
Andrews G.E. and q-Dyson conjecture 54
Andrews G.E., counting triangles with perimeter n 281
Andrews, Euler pentagonal number formula (exercise) 94
Antichain as subset of poset 100
Antimagic square 272
Atiyah M.F. and number of words in quotient monoid 277
Atom of finite lattice 104
Autocorrelation polynomial 267
Backelin J. and number of words in quotient monoid 277
Baclawski K. and core of irreducible poset 176
Baclawski K. and odd composition poset 191
Baclawski K. and topological properties of posets 150
Baker K.A. and dimension of poset 176
Banaschewski Z. and MacNeille completion 176
Barycentric subdivision of finite regular cell complex 121
Bases of vector space for polynomial generating functions 208
Bayer M.M. and Eulerian posets 199
Bedrosian S.D. and counting rooted forests (exercise) 94
Bell E.T. and incidence algebras 149
Bell number 33
Bennett M.K. and Eulerian posets 197
Betke U. and integral convex d-polytopes 288
Bijection 11
Billera L.J. and dimension of vector subspace 199
Binary trees, number of unordered (proposition) 25
Binary trees, properties of (proposition) 24
Binomial coefficients, generating function, approach to 14
Binomial posets and generating functions 140
Binomial posets and subalgebra of incidence algebra (theorem) 144
Binomial posets, definition 142
Binomial posets, literature references 151
Birkhoff Garrett and posets and lattices 149
Birkhoff — von Neumann theorem 93
Bjoemer A. and Bruhat order 199
Bjoemer A. and core of irreducible poset 176
Bjoemer A. and Crapo complementation theorem 184
Bjoemer A. and finite supersolvable lattice 190
Bjoemer A. and topological properties of posets 150
Block of set partition 33
Board and general theory of derangement 71
Bonferroni, over and undercounts for approximation (exercise) 91
Boole G. and partially ordered sets and lattices 149
Boolean algebra of rank n as distributive lattice 107
Bressoud D.M. and tournament (exercise) 95
Bressoud D.M., proof of q-Dyson conjecture 54
Bruggesser H. and Ehrhart polynomial 288
Bruhat order of symmetric group 172 199
Brylawski T., partitions of integer ordered by dominance 192
Butler L. and set of infinite words 191
Butler L., chains of Young diagrams 284
Calculus (formal) for formal power series 7
Calculus of finite differences 36
Canfield E.R. and Stirling number of the second kind (exercise) 57
Cardinality comparison between two finite sets by bijection 79
Cardinality of multiset, definition 15
Carlson F. and power series with integer coefficients 282
Cartier P. and monoid 189
Cartier P., applications of theory of hyperplane arrangements 192
Catalan numbers and a difference equation 62
Catalan numbers and non-crossing partitions 169
Catalan numbers and number of linear extensions of poset 112
Cayley A. and generating function 151
Cellular decomposition of Grassmann variety and partitions of vector space 30
Chain condition 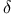 216 216
Chain condition 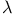 219 219
Chain in distributive lattice 110
Chain, definition of poset as 99
Chain, increasing and R-labeling 133
Chain, saturated 99
Chain-partitionable, finite graded poset 168
Characteristic polynomial of a graded poset 128
Characteristic polynomial of adjacency matrix 242
Chromatic polynomial of a graph 162
Circular factorization, unique 248
CL-labeling, literature references 151
Closure 159
Cluster, L- 266
Clutter, antichain or Spemer family 100
Coatom, of finite lattice 104
Coefficient of n, restricted to finite computation 6
Cohen — Macaulay finite poset and Moebius function 123
Cohen — Macaulay finite poset, definition 123
Cohen — Macaulay posets and lexicographically shellable posets 151
Cohen — Macaulay posets, literature references to discovery of 150
Cohen — Macaulay posets, shellable 193
Coimage 38
Combinations with repetition and multiset 15
Combinatorial interpretation of polynomial, associated with Eulerian poset 139
Combinatorial proof and non-combinatorial proof for same examples 12
Combinatorial proof, definition 11
Combinatorial reciprocity theorem (example) 16 (see also “Reciprocity theorem”)
Comparability graph 168
Comparable elements of posets 97
Compatibility between injectivity and equivalence relation 32
Compatibility between surjectivity and equivalence relation 32
Compatible dual  and P-partition (lemma) 212 and P-partition (lemma) 212
Compatible dual 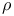 - (lemma) 212 - (lemma) 212
Compatible permutations and descent sets (lemma) 212
Completely fundamental elements of n x n magic squares (lemma) 232
Completely fundamental elements of n x n symmetric magic squares (lemma) 234
Completely fundamental elements of rational polytope (lemma) 236
Composition of n and factorization in free monoids 250
Composition of n, definition 14
Comtet L. and convergence of generating function (exercise) 61
Connected poset 100
Convergent formal power series 6
Convex polytope, integral (corollary) 238
Convex subposet 98
Convolution for locally finite poset 113
Core of irreducible finite poset 155
Counting, subsets of a set 13
Cover function of finitary distributive lattice 157
Cover relations of posets 98
Crapo H.H. and closure relations 183
Crapo H.H., complementation theorem 184
Crimson E. and Moebius function 188
Cvetkovic D.M., rooted tree (exercise) 94
Cycles of permutation defined 17
Cycles, bijection for standard representation (proposition) 18
Cycles, number of (proposition) 18
Cycles, standard representation of 17
Das S.K. and meet-distributive semilattice 178
Davis R.L. and valuation of finite distributive lattice 184
deBruijn N.G., decomposition of permutations of sets (exercise) 47 57
Dedekind R. and posets and lattices 149
Degree of formal power series 6
Dehn — Sommerville equations and Whitney numbers of second kind (proposition) 136
Dehn — Sommerville equations, literature references 151
Deligne P. and Weil conjectures 279
Delta-chain condition, definition 216
Delta-chain condition, theorem 218
Denominator of a rational vector 236
Deodhar V.V. and Bruhat order 199
Derangement problem and use of Principle of Inclusion-Exclusion 67
Derangement, definition 67
Derivative (formal), definition for formal power series 7
Descent set , number of permutations (proposition) 22
| Descent set and Inclusion-Exclusion 69
Descent set of multiset permutation 25
Descent set of permutation 21
Determinants 82
Determinations, definition by example 1
Dickson L.E., binomial coefficients and primes (exercise) 53
Difference of f, formula for k-th 37
Difference operator 36
Difference table and bases for polynomials 209
Difference table for finite differences of a function 37
Digraph 241 293
Dilworth R.P. and modular lattice 186
Dilworth R.P. and order ideals 182
Dilworth, theorem of 110
Dimension of finite poset 176
Dimers 273
Diophantine equations, linear homogeneous 221
Direct product of two posets (figure) 101
Direct product, twisted (figure) 175
Dissects, literature references 151
Distinguishable, elements of set 31
Dominance, definition of order by 166
Doob M., rooted tree (exercise) 94
Double partition 77
Doubly stochastic matrices 240
Dowling lattice 191
Dowling T. and uniform poset 191
Dowling T. and Whitney number inequalities 185
Down-set, subset of poset 100
Dreesen B. and comparability graph 194
Dual for Principle of Inclusion-Exclusion 66
Dual of Moebius inversion formula 116
Dual of poset 101
Duality theorem, master for Eulerian posets 138
Duffus D. and core of irreducible poset 176
Dumont D., finite differences (exercise) 61
Durfee square, definition for partition 58
Dwork B. and Weil conjectures 279
Dyson, P.J. and q-Dyson conjecure 34
Edelman P.H. and Bruhat order 199
Edelman P.H. and maximum Moebius function 187
Edelman P.H. and meet-distributive meet-semilattice 179
Edelman P.H. and non-crossing partitions 197
Edelman P.H. and odd composition poset 191
Edelman P.H., counting certain posets 178
Edelman P.H., simple reduction of permutation set 199
Edelman P.H., weak Bruhat order 199
Edwards R.D. and finite regular cell complex (proposition) 150
Ehrhart polynomial 238
Ehrhart quasi-polynomial of rational polytope 235
Eigenvalue of adjacency matrix 242
Eigenvalue of circulant matrix 273
Enting I.G. and chromatic polynomial 292
Equivalent sets 31
Euler characteristic, definition of reduced 120
Euler number, count of alternating permutations 149
Euler pair 48
Euler pentagonal number formula 89
Euler's totient function 62
Euler's totient function, exercise 48 161
Eulerian lattice, a fundamental example of 136
Eulerian number as count of excedances 23
Eulerian number f 209 22
Eulerian polynomial f 209 22
Eulerian polynomial for multiset 26
Eulerian posets and zeta polynomial (proposition) 135
Eulerian posets, definition 122 135
Eulerian posets, figure 138
Eulerian posets, literature references 151
Excedance of permutation 23
Exceptional set and rational functions (proposition) 205
Exponential generating function and binomial posets 141
Exponential generating function, definition 3
Extensions, number of linear, for posets (figure) 111
Extensions, number of, and chains 110
Extensions, number of, and permutations 112
Extensions, number of, and recurrence 112
Factor of word 266
Factorial function of P as number of maximal chains 142
Fall as element of permutation 24
Farmer F.D. and poset of normal words 199
Fatou P. and Fatou's lemma 275
Fatou's lemma and primitive series 275
Fences or zig-zag posets 109
Ferrers boards 74
Ferrers boards wiih equal rook polynomials 75
Ferrers diagram of a partition of n 29
Ferrers diagram of conjugate partition 39
Fibonacci number, Eulerian posets and dimension of vector subspace 172
Filter, order ideal subset of poset 100
Finitary distributive lattice and Pascal's triangle 112
Finitary distributive lattice, definition of 107
Finite difference, to define excluded objects from set (proposition) 68
Finite graded poset, Eulerian 122
Finite graph, definition 293
Finite graph, edges 293
Finite graph, loop 293
Finite graph, simple 293
Finite graph, vertices of 293
Finite regular cell complex, definition 121
Finite regular cell complex, figures 122
Fishbum P.C. and dimension of poset 176
Fixed point set, counted in terms of weight function 80
Fixed points for permutations 68
Foata D. and monoid 189
Foata D., Forest and Ehrhart polynomial 272
Foata D., multiset permutations 57
Forests 93
Forests, rooted 89
Forests, spanning 93 273
Formal power series as integral domain 4
Formal power series, definition 3
Formal power series, primitive 275
Formal power series, treated as functions 8
Formal power series, validity of identities (example) 5 6
Frankl P., conjecture on cardinality of dual order ideals 186
Free monoids, factorization in 247
Free R-module 167
Freely generated submonoid 247
Freely generated submonoid, very pure 248
Freese R. and complements in a finite lattice 184
Fundamental property of rational functions, simplification (corollary) 204
Fundamental property of rational functions, theorem 202
Gale's evenness condition and faces of convex polytope 199
Ganter B. and modular lattice 186
Garisa A.M. and chain-partitionable posets 193
Garisa A.M. and vector partitions 282
Gaussian polynomial or q-binomial coeffient 26
Geissinger L. and a convex polytope, associated with a poset 199
Geissinger L. and valuation of finite distributive lattice 184
Generating function and adjacency matrix (theorem) 242
Generating function and binomial posets 140
Generating function and closed walks (corollary) 243
Generating function and completely fundamental elements (theorem) 228
Generating function and number of P-partitions 216
Generating function and quasi-generators (corollary) 227
Generating function and weighted edges of digraph 258
Generating function for evaluating counting function 3
Generating function for monoid 222
Generating function for monoid, specialization (theorem) 231
Generating function for number of closed walks of length n 244
Generating function for number of partitions of n 38
Generating function for restricted partitions 39
Generating function for simplicial monoids (corollary) 227
Generating function, advantages of using 10
Generating function, chromatic 142
Generating function, cluster 267
Generating function, doubly-exponential 141
Generating function, Eulerian 141
Generating function, exponential 141
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



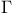 , triangulation of pointed convex polyhedral cone
, triangulation of pointed convex polyhedral cone 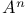 (theorem)
(theorem) 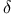
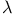
 and P-partition (lemma)
and P-partition (lemma) 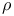 - (lemma)
- (lemma)