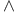|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Azcarraga J., Izquierdo J. — Lie groups, Lie algebras, cohomology and some applications in physics |
|
|
 |
| Предметный указатель |
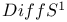 332 345 332 345
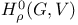 233 233
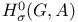 219 219
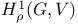 234 234
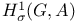 220 220
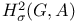 220 220
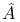 -roof genus 147 391 -roof genus 147 391
 -symmetry 312 314 -symmetry 312 314
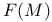 -linearity in -linearity in 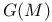 338 338
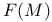 -valued algebra cohomology 262 -valued algebra cohomology 262
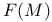 -valued cochains on G 226 -valued cochains on G 226
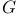 -valued differential forms 59 -valued differential forms 59
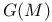 337 337
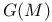 , Kac — Moody 334 340—345 349 397 , Kac — Moody 334 340—345 349 397
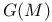 , Virasoro 332 345—351 354 , Virasoro 332 345—351 354
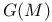 , Weyl — Heisenberg 343 , Weyl — Heisenberg 343
 -invariant vector field 9 -invariant vector field 9
 -related tensor fields 35 -related tensor fields 35
 -related vector fields 8 37 -related vector fields 8 37
1-jet prolongation 282 291
1-jet section 282
Abelian U(1) or axial anomaly 366—372
Actions of a Lie group 4
AdG-invariant polynomials 104 105 385
Adjoint action 4 27
Adjoint representation of a group AdG 27 65
Adjoint representation of an algebra 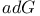 66 66
Algebra cocycles 232
Algebra cocycles, simple cases 233
Algebra of equal-time charges 340
Algebra of vector fields 7
Anomalies, abelian or U(1) 366—372
Anomalies, cancellation 385—387
Anomalies, chiral or non-abelian 366 379—417
Anomalies, consistency (Wess — Zumino) condition 366 382 395
Anomalies, finite and infinitesimal versions 395
Anomalies, global (Witten's) 365
Anomalies, safe groups or algebras 365 385
Anomalous divergence 368—371
Anomalous Gauss law 396—397
Anomalous quantum theory 366
Anti-homomorphism 4 12 13
Anti-instanton solutions 127 130
Anti-self-dual gauge fields 49 127
Anti-unitary operators 159
Anticommuting variables 70
Antiderivation 35—36
Antisymmetric tensor field 32
Antisymmetric tensors, higher order 125
Associated, bundle 26
Associated, principal bundle 28
Associated, tensor bundle 26
Associated, vector bundle 25
Associativity breaking 187
Associator 279
Atiyah — Singer theorem 143
Atlas 2
Baker — Campbell — Hausdorff group 333 363
Banach space 332
Bargmann, Galilei two-cocycle 171
Bargmann, superselection rule 157
Betti numbers 43 45
Betti numbers of groups 78—80 248
Bi-invariant forms 63 80 248
Bi-invariant measure 58 60
Bi-invariant measure on GL(n, R) 66—67
Bi-invariant metric 64—65
Bianchi identity 92 94 98 127
Bott's periodicity 74
Boundary of a manifold 42
Boundary operator 8 46
BRST cohomology 249—253
BRST cohomology, formalism for gauge algebras 378
BRST cohomology, n-cochains 251
BRST cohomology, operator 250 308—309 407
BRST cohomology, transformations 378
Bundle 12
Bundle of Lie algebras 27 363
Bundle of Lie groups 27
Bundle of linear frames 26 30 84 96
Bundle of orthonormal frames 30 96
Bundle of Yang — Mills connections 361 363
Bundle, 1-jet 282
Bundle, associated 25—26 28
Bundle, base manifold 13
Bundle, coordinate 16
Bundle, cotangent 23
Bundle, diffeomorphisms 30
Bundle, equivalent 30
Bundle, examples 16—20
Bundle, homomorphism 28
Bundle, instanton 21 100 149
Bundle, local triviality 13—15
Bundle, morphism 29
Bundle, principal 13
Bundle, projection 13 22
Bundle, reduced 30 96
Bundle, structure group 13
Bundle, subbundle 30
Bundle, tangent 22
Bundle, tensor 23
Bundle, tensor product 23
Bundle, total manifold 13
Bundle, trivial 15—16 29
Bundle, vector 22
Bundle, Whitney sum 23
Bundles over contractible manifolds 20
Bundles over spheres 21
Canonical form on a Lie group 59
Canonical parallelism 60
Cartan calculus 31—43
Cartan decomposition 37
Cartan homotopy formula 110
Cartan homotopy operator 110 401
Cartan structural equation 92
Cartan — Killing tensor 63—65
Casimir invariants 80 249 385
Casimir operators 385
Casimir polynomials 248
Cech cohomology 21
Central charge 224 242 297
Central extension 162—163 168 189—192 221 238 295 301 341 347
Centre of a G-kernel 205
Chain rule 6
Characteristic class 104—120
Characteristic function 42
Characteristic module 292
Characteristic number 104
Characteristic polynomial 105
Characteristic vector field 165
Charge densities 319 338
Chern character form 114 391 400 408
Chern characters 114—115
Chern classes 104 111—112
Chern classes and infinite-dimensional Lie algebra cohomology 335
Chern classes and instantons 127
Chern classes, splitting principle for 115
Chern forms 112 385
Chern numbers 113
Chern — Simons form 109 116 391 418—420
Chern — Simons form, gauge transformation properties 118
Chern — Simons secondary class 109
Chern — Simons secondary class, generalization 110
Chern — Weil theorem 106 131
Chevalley — Eilenberg (p+2)-cocycles on 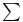 314 314
Chevalley — Eilenberg cohomology 246—248 252 287 290 326 335 415
Chevalley — Eilenberg cohomology on 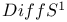 351 351
Chiral fermionic fields 366 379 380
Chiral or axial currents 368
Chiral superfields 73
| Christoffel symbols 90 95
Classical anomalies 303
Classical compact groups 74
Clifford algebra 145
Coadjoint action 178
Coadjoint orbits 176 181 184
Coadjoint representation ad* of 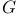 66 66
Coadjoint representation Ad* of G 66 174
Coboundary operators, left action 216 227 231
Coboundary operators, right action 216 228 232 375
Coclosed form 53
Codifferential  46—47 49—53 46—47 49—53
Codifferential  as a divergence 50 as a divergence 50
Coexact form 53
Cohomological descent 303 308—309 394 398—416
Cohomological descent, ambiguity 405
Cohomological descent, cochains and coboundary operators 398—399
Cohomological descent, equations 403—408
Cohomological descent, non-triviality of the cocycles 415
Cohomology and classical mechanics 281 297—308
Cohomology of groups 215—229
Cohomology of Lie algebras 230—263
Cohomology on G(M), 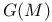 374—377 374—377
Cohomology on infinite-dimensional Lie algebras 335 348
Cohomology, Cech 21
Cohomology, Chevalley — Eilenberg 246—248 252 287 290 326 335 415
Cohomology, de Rham 43 80 107 248 287
Cohomology, equivariant 54 81
Cohomology, groups for semisimple algebras 242—243
Cohomology, groups of a compact group 254
Commutators 341
Complete Lorentz group L, extensions 275—279
Composite mapping theorem 7
Conformal, algebra 356
Conformal, anomaly 348 357 366
Conformal, group 354
Conformal, group in two dimensions 356
Conformal, invariance and self-duality 121
Conformal, Killing vector 355
Connected sum 136
Connection 84—95
Connection on  100 100
Connection on a Lie group 100
Connection, affine space 90
Connection, flat 91 93
Connection, form 88
Connection, interpolating family of 107
Connection, linear 95
Connection, local representatives 89—90
Connection, reducible 96
Consistent anomalous theories 416—417
Consistent anomaly 381 395
Construction of the extensions 272
contact forms 283
Contractible manifold 44
Contractions and group cohomology 192—197
Contravariant vector field 31
Convex set 332
Coordinate bundle 16
Coset spaces 17
Cotangent bundle 23
Coulomb gauge 361
Covariant conservation 380
Covariant derivatives 95 361
Covariant derivatives on superspace 73
Covariant differentiation 40
Covariant divergence 385
Covariant vector field 23 31
Covector field 23
Critical trajectories 285
Cross section, global 15
Cross section, local 13
Cross section, natural 14—15
Crossed homomorphism 222
Current algebra 338 345
Curvature two-form 91 101 324
d,  and and  : relations between them 51 : relations between them 51
De Rham cohomology 43 80 107 248 287
de Rham cohomology on spheres 44
de Rham cohomology, coboundaries 43
de Rham cohomology, cocycles 43
de Rham cohomology, groups 43
de Rham cohomology, ring 45
de Rham complex 137 139
Derived series 243
Descending central series 243
Descent equations 403—408
Determinant bundle 394
Differentiable exponents 161
Differentiable manifold 2
Differentiable mapping 8
Differential forms 23—24 31—43
Differential mapping 6
Differential structure 2
Differential structure, exotic smooth structures 131
Dilatations 356
Dirac brackets 319
Dirac string 123
Dirac's quantization condition 125
Direct product of groups 192 223
Division algebras 21
Double cohomology sequences 308—309 322 403—404
Dual tensor 98
Dynamical groups 173
Effective action 4
Eilenberg — MacLane theorem 272
Electric current 121
Elliptic complex 141
Elliptic complex, classical 144
Elliptic complex, two-term 142
Elliptic operator 140 369 381
Embedding 29 30
Equivariant form 102—103
Equivariant function (G-function) 28
Euclidean group 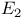 254 254
Euclidean space 387
Euler class 104 135
Euler form 135
Euler — Poincare characteristic 44—45 78 136 138
Euler — Poincare characteristic for the spheres 44
Euler — Poincare characteristic of a Lie group 80
Evolution space 282 290
Evolution space, enlarged 293
Exact sequences 199—201
Exotic smooth structures 131
Exponential groups 254
Extended Galilei algebra 170 182 286
Extended Galilei groups 158 169 206 300
extended objects 125
Extended objects, supersymmetric 313 315—324
Extendible G-kernel 204 268
Extensions of G by an abelian group A 221—223
Exterior covariant derivative 91 324
Exterior derivative d 35
Exterior functional derivative 316 352
Exterior product 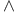 32 32
External automorphisms 203
f-orbit 4
Factor system 199 209—211
Faddeev — Popov ghost fields 250 378
Faithful action 4
Fermionic functional 367
Fermionic functional, determinant 380 387—390
Fermionic functional, measure 367 380
Field strength F, electromagnetic 48
Field strength F, Yang — Mills 98
Forms 23—24 31—43
Forms, closed 43 139
Forms, coclosed 53 139
Forms, coexact 53
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



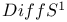
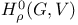
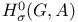
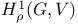
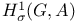
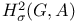
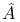 -roof genus
-roof genus  -symmetry
-symmetry 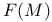 -linearity in
-linearity in 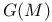
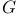 -valued differential forms
-valued differential forms  -invariant vector field
-invariant vector field 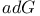
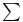


 : relations between them
: relations between them