|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Azcarraga J., Izquierdo J. — Lie groups, Lie algebras, cohomology and some applications in physics |
|
|
 |
| Предметный указатель |
Forms, exact 43
Frame bundle 26 30 84 96
Fredholm operator 141 369
Free action 4
Free differential algebra 401 408
Free module 10
Freudenthal suspension theorem 76
Fujikawa method 366
Full quantum mechanical Poincare groups 279
Functional exterior derivative d 316 352
Functional vector fields 317 336 352
Fundamental vector field 88
G-kernel 204 264
G-kernel, third cohomology group 266
Galilean invariance 154
Galilei algebra 170 182
Galilei group 153 287
Galilei group, adjoint and coadjoint, representations 181 183
Galilei group, cohomology 155 168 261
Gamma matrices, Euclidean 145 367
Gamma matrices, Minkowskian 71 146 315
Gauge algebra bundle 27
Gauge algebra coboundary operator 376
Gauge algebra cohomology 374—377 401
Gauge anomalies 360—423
Gauge fixing equation 361
Gauge Functions 97
Gauge group 30 362
Gauge group bundle 27
Gauge group, coboundary operator 375
Gauge invariance principle 99 360
Gauge transformations 27 334 361 379
Gauge transformations, based 363
Gauge transformations, infinitesimal 27 97—98 373
Gauge transformations, large and small 130
Gauge-variant function 298
Gauss law constraints 396
Gauss — Bonnet theorem 136
Gauss' theorem 43
Gaussian cut-off 369 382
Gelfand — Fuks theorem 348
Gelfand — Fuks two-cocycle 349
Gell-Mann — Levy equations 339
General covariance 99
Generalized electrodynamics 125
Generating functional 361 379—380
Genus 45
Ghost number 251
Ghost parameters 249 308 378
Ghosts as Maurer — Cartan forms 252 379
Graded, commutation rules 72
Graded, derivation 35—36
Graded, Lie algebras 72 253
Graded, Lie groups 250
Graded, Poisson brackets 321
Grassmann manifolds 17
Grassmann variables 70 73 287 368
Gravity as a gauge theory 99
Gravity, two-dimensional 351 354
Green — Schwarz superstring action 314
Gribov ambiguity 361 365
Group coboundary operator 216 227—228 375
Group extension 199 201—213
Group extension, bundle description 207
Group extension, characterization 209—210
Group extension, construction 211—213 270—275
Group extension, equivalence 205
Group extension, G-kernel 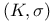 204 264 204 264
Group extension, Galilei 169 300
Group extension, group law 211
Group extension, obstruction 264
Group extension, super-Poincare (N=2) 224—225
Group extension, supertranslations 223—224
Group extension, Weyl — Heisenberg 163
Group n-coboundaries 219
Group n-cocycles 219
Group(s), 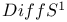 332 345 332 345
Group(s), 'local' 335
Group(s), Betti numbers of 78—80
Group(s), conformal 354
Group(s), coordinate transformations 30
Group(s), DiffM 4 331
Group(s), dihedral 278
Group(s), Euclidean (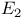 ) 254 ) 254
Group(s), exceptional 75 79
Group(s), Galilei 153 287
Group(s), gauge 30 362
Group(s), general Lie 332
Group(s), GL(n, R) 12
Group(s), homotopy groups of 73—75
Group(s), O(n) 74
Group(s), Poincare 4 191 193 195 287
Group(s), quaternionic 278
Group(s), rotation 68
Group(s), SO(2, 1) 194
Group(s), SO(3, R) 68
Group(s), SO(n, R) 74
Group(s), Sp(n) 74
Group(s), Spin(n) 144
Group(s), SU(2) 18 403
Group(s), SU(n) 75
Group(s), Super-Poincare 225
Group(s), supertranslations 71 223—224
Group(s), U(n) 74
Group(s), USp(2n) 74
Haar measure on a Lie group 57
Hamiltonian vector field 173
Harmonic forms 52
Harmonic forms on  54 54
Harmonic oscillator algebra 243
Hausdorff manifold 2
Heat kernel regularization 369 382
Higher cohomology groups, meaning 279—280
Hodge (star) operator 47
Hodge decomposition theorem 53
Hodge — de Rham theory 52—54 137
Homogeneous space 4
Homology 46 80
Homotopy axiom for de Rham cohomology 45
Homotopy groups for spheres  75 75
Homotopy groups for the classical compact groups 74
Homotopy groups for the exceptional groups 75
Homotopy sequence 76—77 364
Hopf bundle 100
Hopf fibrings 20 129
Hopf invariant 21
Hopf mapping 18
Horizontal lift 85—86
Horizontal subspace 85—86
Horizontal vectors 85
Immersion 30
Incompressible vector field 39
Index of the Dirac operator 147
Index, analytical 137 139 142
Index, theorems 137
Index, theorems, Atiyah — Singer 143
Index, theorems, de Rham complex 138
Index, theorems, spin complex 147—149 369
Index, topological 138 142
Infinite-dimensional Lie algebras 3 23 331—335
Infinite-dimensional Lie groups 3 331—335
Inner automorphisms 202
Instanton bundles 21 100 149
Integrable form 42
Integration of forms 41
Interior of a manifold 42
Interior product 36
Invariant connections 100
Invariant forms 54—58
Invariant forms on 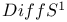 352 352
| Invariant forms on the extended Galilei group 169 172
Invariant forms on the rotation group 69
Invariant measure on triangular matrix groups 67
Invariant polynomial 105 247
Invariant symmetric tensors 385
Invariant vector fields 9—10
Invariant vector fields on GL(n, R) 12
Invariant vector fields on the extended Galilei group 169 172
Invariant vector fields on the rotation group 69
Invariant volume element  47 47
Irreducible symmetric tensors on 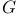 248 248
Isometry 52
Jacobian determinant and anomalies 369 380
Jet bundles 282
Kac — Moody algebra 334 340—345 349 397
Killing equations 39
Killing tensor 63—65 245
Killing vector field 39
Kinematical groups, classification 291
Kirillov term  111 179 181 111 179 181
Kronecker symbol  32 32
kth homotopy group 73
Kuenneth formula 45
Lagrange bracket 166
Lagrange equations 284
Lagrangian form 283
Lagrangian form, quasi-invariant 290 317
Lande paradox 156
Laplace — de Rham operator 51
Laplacian 51
Laplacian and index theorems 139
Leading symbol of 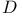 140 140
Left action 3 5
Left-invariant form on a Lie group 55
Left-invariant vector field 9
Left/right translation 3
Leibniz's rule 35
Levi — Mal'cev theorem 243
Levi — Mal'cev theorem, splitting 290
Levy — Leblond theorem 299
Lie algebra 3 5—8
Lie algebra, cohomology 230—236
Lie algebra, cohomology, coboundary operator 231—232
Lie algebra, cohomology, vs. Lie group cohomology 238—239 253—262
Lie algebra, extensions 234
Lie algebra, extensions, equivalent 235
Lie algebra, n-coboundary 231
Lie algebra, n-cocycle 231
Lie derivative 37
Lie group 2—3
Lie group as a principal bundle 16
Lie's second theorem 11
Lie's third theorem 333
Line bundle 21 115
Liouville form 174 286
Liouville theorem 52
Little group 4
Local algebras 338
Local exponents 159 162 238
Local exponents of 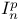 192 192
Local exponents of a semisimple group 191
Local factors 159—160
Local factors, equivalent 160
Local functionals 395
Local gauge group 97 331 334 335 362
Local triviality 13—15
Locally convex space 332
Locally Hamiltonian vector field 173 332
Long exact sequences 280
Loop algebra 334
Loop algebra, two-cocycle 341—343
Loop groups 331 334 341
Loop groups, generalized 331
Loop superspace 316
Lorentz group 275
Magnetic current k 121
Magnetic monopole 100 120—125
Magnetic monopole, Lagrangian 324—329
Magnetic monopole, quantization condition 125
Magnetic monopole, three-cocycle 189 261
Majorana spinors 71 223
Manifold 2
Manifold with boundary 42
Manifold, compact 44
Manifold, contractible 44
Manifold, cotangent 23
Manifold, Hausdorff 42
Manifold, orientable 30 39
Manifold, paracompact 42
Manifold, parallelizable 27—28 44 60
Manifold, Riemannian 96
Manifold, tangent 22
Manifold, universal covering 18
Massive superparticle 311—312 324
Mathematics and physics 125—126
Matter fields 25 95 97
Maurer — Cartan equations 58 252 352
Maxwell equations 120
Maxwell equations in D-dimensional space 125
Mechanics and cohomology 281 297—308
Metric tensor 32
Metricity condition 146
Minkowski space 287
Module of cross sections 22
Moduli space 131 151
Moebius strip 27
Moebius transformations 349
Momentum mapping 173
Multi-instantons 130
n-cochains on G 215
n-cocycles as differential forms 246
n-dimensional cochains on 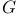 231 231
n-extended superspace 224 311
Natural cross section 14—15
Naturalness 36—40
Newtonian mechanics 290—297 308
Newtonian mechanics, 'anomaly' 300 308
Nilpotent groups 254
Nilpotent groups, algebras 243
Noether charges 285 312
Noether charges, densities 319 338
Noether theorem for mechanics 285
Non-abelian anomaly 366 379—417
Non-abelian anomaly and D+2 index theorem 388
Non-abelian anomaly and second cohomology group 396
Non-abelian anomaly and topology 387—394
Non-abelian anomaly from the abelian anomaly 387
Non-abelian anomaly in D=2,4 dimensions 408—415
Non-abelian anomaly, local properties 394
Non-associative group 279
Non-associative systems 279
Non-commutative geometry 168
Non-trivial WZW terms and quantization 290 412
Normalized factors 209
Normalized section 209
Nth cohomology group of 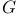 232 232
Nth cohomology group of G 219
Null section 23
Octonions 20—21
One-parameter group of diffeomorphisms 38
One-parameter subgroup 62
Orbit space 363 393
Orbit space, non-trivial topology 364—365 388
Ordinary variational principle 284
Orientability 104
Orientable manifold 30 39
Oriented frames 30 96
Orthonormal frames 30 96
Palais' Theorem 7
Paracompact manifold 42
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 )
)