|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Azcarraga J., Izquierdo J. — Lie groups, Lie algebras, cohomology and some applications in physics |
|
|
 |
| Предметный указатель |
Parallel transport 84
Parallelizable manifold 27—28 44 60
Parallelizable spheres 28
Particle in a magnetic field B 294
Particle-antiparticle conjugation matrix 71
Partition of unity 42
Period 46
Pfaffian 134
Physics and mathematics 125—126
Planck manifold 167
Poincare duality 44
Poincare group 4 191 193 195 287
Poincare polynomials 78
Poincare — Cartan form 283 297 308
Poincare's lemma 43—44
Poisson algebra 300
Poisson algebra, brackets 165 190 295
Poisson algebra, manifold 166
Polarizations 167
Polyakov — Wiegmann action 354
Pontrjagin classes 104 131—133
Potential form 43
Prequantization 167
Presymplectic manifold 173
Primitively harmonic form 53
Principal bundle 13—17
Principal bundle of linear frames 26 30 84 96
Principal bundle, homomorphism 29
Principal homomorphism (derivation) 222
Principal symbol of 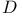 140 140
Product of extensions 271
Product of forms 49
Product of G-kernels 270
Projectable forms 105
Projectable vector field 86
Projective representations 157
Projective spaces 17 20
Pseudo-differential operators 143
Pseudoextension 193
Pseudotensorial forms 91
Pull-back 9 33 35
Push-forward 9 33
Quantization form 165
Quantomorphism 167
Quantum Galilei group 191
Quantum lifting 167
Quantum manifold 165 167 190
Quasi-invariance 153 170 289—294 303—305 317
Quasi-invariance and non-trivial group cohomology 303
Quaternions 20—21
r-jet 24
Radical of a Lie algebra 243
Ray 154
Ray, operators 159
Ray, representation 157 160
Ray, representation, finite-dimensional 163
Reconstruction theorem 15
Reduced bundles 30 96
Reduced join 388
Relativity group 152
Riemannian connection 96
Riemannian manifold 96
Riemannian structure 30
Right action 3 6
Right-invariant vector field 10
Rigid transformations 334 360
Rotation group 68
Rotation group, adjoint representation 69
Rotation group, group law 68
Rotation group, invariant measure 70
Rotation group, Killing form 70
Safe groups or algebras 365
Schwinger terms 340 344 379 397
Schwinger terms and Kac — Moody algebra 410
Schwinger terms in D=2,4 dimensions 408—410 413—414
Schwinger terms, classes 398
Self-dual gauge fields 49 127
Self-duality condition, conformal invariance 127
Semidirect extension 222—223 237 275 287
Semisimple Lie algebra 63
Simplicial cohomology 46
Simplicial homology 46
Smashed product 388
Solvable groups 254
Solvable Lie algebra 243
Sphere groups 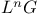 331 331
Spin complex 144—149
Spin complex, index 147—149 369
Spin connection 146
Spin structure 104 144
Spin(n) 144
Spinor bundle 144
Splitting extension 222
Splitting principle 115
Stable homotopy groups 74
Standard model 97 385
Star (Hodge) operator 47
Stiefel — Whitney classes 104 144
Stokes' theorem 42
String 313
Structure constants 5 11
Structure constants from the central extension two-cocycle 238 302
Structure group 13
SU(1, 1) principal bundle 20
Subbundle 30
Sugawara construction 351
Super Lie groups 70
Super-Poincare algebra 73 312
Super-Poincare algebra, group 225
Superalgebras 72
Superalgebras and extended objects 315—323
Superfields 73
Supermanifold 70
Supermembrane 313
| Superspace 71 223
Superstring 313
Supersymmetric extended objects 313 315—324
Supersymmetry 71 224
Supersymmetry algebra 73
Supertranslation group 71 224
Symmetric multilineal forms on 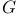 80 80
Symmetry transformation of a dynamical system 285
Symmetry transformation, global vs. local 334
Symplectic, coboundary 176
Symplectic, cocycle on 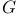 177 178 241 177 178 241
Symplectic, cocycle on G 175 178 241
Symplectic, cohomology 173 175—179
Symplectic, diffeomorphisms 186 332
Symplectic, form 165
Symplectic, manifold 165
Symplectic, orbits 176 178
Symplectic, structure 179
Symplectic, transformation 165
Symplectomorphisms 186
Tangent, 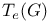 6 6
Tangent, bundle 22
Tangent, mapping 6
Tangent, space 22
Tensor bundle 23
Tensor derivation 37
Tensor field 23 31—32
Tensor product bundle 23
Tensorial forms 91 94
Three-coboundary 268
Three-cocycles 186 189 245 261 264
Todd class 144
Topological charges 321
Topological extension 324
Topological index 138 142
Topological invariants 104
Topological quantization 290 412
Topological subgroup 16
Topological terms 289
Torsion 80
Total Chern class 112
Total Chern form 112
Total manifold 13
Total Pontrjagin class 133
Transgression formula 109 401
Transgression operator 109
Transition functions 15 21 25 89
Transition functions, cocycle condition 16 22 99
Transition functions, equivalent 16
Transitive action 4
Triangle equality 110
Trivial action 4
Trivial bundle 15—16 29
Triviality 27—31
Triviality of 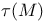 23 23
Triviality of a principal bundle 15
Triviality of associated bundles 27 29 31
Trivializing section 207
Twisted complex 144 148—149
Twisted complex, de Rham 148
Twisted complex, spin 148 366 369
Two-coboundary 161
Two-cocycle condition 158
Ultralocality 323
Unimodular groups 58 60
van Est theorem 254
Variational principles 24 283
Vector bundle 22
Vector bundle morphism 29
Vector field 5 8 22 31
Vector field, fundamental 88
Vector field, incompressible 39
Vector field, invariant 9—10
Vector field, valued forms 59
Vector field, vertical 86
Vertical bundle automorphisms 30 362
Vertical subspace 85
Vertical vector field 86
Virasoro algebra 332 345—351 354
Volume form 39
Wavesection 125
Weil homomorphism 106 108
Weinberg — Salam standard model 97 385
Wess — Zumino condition 288—289 366 382
Wess — Zumino condition as one-cocycle 395
Wess — Zumino forms on a Lie group G 289 292 297
Wess — Zumino Lagrangian density 317
Wess — Zumino terms 289 292 309
Wess — Zumino terms and the supersymmetric extended objects 312 314—318
Wess — Zumino terms in D=2,4 dimensions 411 414 416
Wess — Zumino terms on 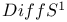 354 354
Wess — Zumino terms, topologically non-trivial 290 329
Wess — Zumino — Witten model 351 357
Weyl differential operators 147
Weyl fermionic fields 366 379
Weyl-Heisenberg group 163 180
Weyl-Heisenberg group, algebra 164 243
Whitehead's Lemma 243 334 343 349
Whitehead's Theorem 244
Whitney sum bundle 23
Wick rotation 367
Winding number 119 124 129 328 389 392
Witt algebra 345 354 357
Witten's global anomaly 365
Yang — Mills action 126
Yang — Mills action, euclidean 127
Yang — Mills fields 97 99
Yang — Mills instantons 126—131
Yang — Mills instantons, number 119 130 149
Yang — Mills instantons, size 129
Yang — Mills instantons, solutions 127—129
Yang — Mills orbit space 363
Yang — Mills potentials 90 361 372
Yang — Mills theories 250 366
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте