|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Torretti R. — Relativity and Geometry |
|
|
 |
| Предметный указатель |
Law of motion in General Relativity 176 figures
Law of Motion, Geodesic see “Geodesic Law”
Laws of Coulomb 35
Laws of Motion (Newton), First see “Principle of Inertia””
Laws of Motion (Newton), Second 9 19 29 55 107 284
Laws of Motion (Newton), Third 9 19 43 51 55 83 107 287
Laws of physics and Relativity Principle 30 figure 54 65
Leavitt, H. 203
Lee, A.R. 298 367
Leibniz, G W. 33 167 285 367
Lemaitre, G. 204 333 367
Length contraction, relativistic 67 figure 97
Length of curve 94
Length of moving rod 296 note 1 to section 3 5
Lense, J. 200 367
Lerner, R.G 296 335 367
Levi — Civita connection 101 188 279
Levi — Civita connection, components 281
Levi-Civita, T. 143 146 176 187 188 194 319 326 367 373
Levine, M.W. 311
Levy-Leblond, J.M. 76 297 298 352 367
Lewis, G N. 2 70 112 296 367
licf (local inertial comoving frame) 115
Lichnerowicz, A. 284 305 308 367
Lie algebra 268
Lie bracket 268
Lie derivative 101 261—262 268
Lie group 268 269
Lie group, adjoint representation 269
Lie group, defined 288 note 12
Lie, S. 288 297 333 367
Lifshitz, E M. 287 293 345 366
Lift 270 349
Light 37 40—42 49 50 51 84 137 290 312
Light speed and gravitational potential 138 140
Light speed as maximum signal speed 71
Light velocity, in moving refracting medium 70 (see also “Aether drag”)
Light, aberration of 41 70 291 note 300
Light, deflection by gravity 135 138 173 311 322
Light, propagation of 312 note 13 note
Lindsay, R.B. 293 367
Line element, de Sitter empty universe 329 note 27
Line element, of arbitrary Riemannian manifold 101
Line element, of surface 313 note 4
Line element, Robertson — Walker 207
Line element, Schwarz-schild 335 note 2
Line element, static Einstein universe 329 note 24
Line of force (Faraday) 36
Linear connection 272
Linear connection, complete 278
Linear connection, incomplete 212
Linear connection, metric 279
Linear connection, symmetric or torsion-free 188 277
Linear connection, Weyl’s definition 188 (see also “Levi — Civita connection”)
Lobachevsky, N.I. 1 283 333 340
Locally Minkowskian 145 314
Lorentz chart 54 56 227 296
Lorentz chart, local 136 147
Lorentz chart, matched Lorentz charts 57 295
Lorentz force 43 113 116 323
Lorentz group 6 62 89 283 295 note 302
Lorentz group, general homogeneous 280
Lorentz group, homogeneous 6 63—65 86 295
Lorentz group, orthochronous 64
Lorentz group, proper 64
Lorentz metric 93 314
Lorentz metric, compatible with linear connection 192
Lorentz metric, topology for set of Lorentz metrics on a given 4-manifold 337 note 17
Lorentz tetrad field 102
Lorentz transformation of electromagnetic field components relative to matching charts 109
Lorentz transformation, equations for matching charts (“coordinate systems in standard position”) 61 84
Lorentz transformation, equations for non-matching charts with common origin 62
Lorentz transformation, linearity of 57 71—76 297 note 298 299
Lorentz, H.A. 3 42—47 48 70 83 84—85 86 87 131 162 176 184 291—292 294 296 301 302 306 307 309 310 319 367 368
Lovelock, D. 160 305 308 317 318 321 323 368 373
LP (Light Principle) 54 (see also under “ Principle of Constancy of Light Velocity”)
MacCallum, M.A.H. 347 368
MacCullagh, J. 290 368
Mach, E 196 197 201 202 287 292 319 320 328 368
Machian effects in Einstein’s theories of gravity 196 figure 200 328
Machian solutions to Einstein field equations 331 note 43 332
Mach’s principle 196—202 328 note 331 note
Mach’s Principle, dismissed by Einstein 201 202
Mach’s Principle, inimical to General Relativity 199—201
Mach’s Principle, opposed to Equivalence Principle 200
MacLane, S. 284 348 368
Malament, D. vi 129 229—230 347 368
Manifold 2 72 257 348
Manifold, analytic 288 note 12
Manifold, complex 348 note 3
Manifold, flat 145
Manifold, locally Minkowskian 145
Manifold, orientable 257
Manifold, parallelizable 93 99 265
Manifold, product 258
Manifold, real n-dimensional 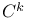 -differentiable 257 (see also under “Affine” “Conformal” “Projective” “Riemannian”) -differentiable 257 (see also under “Affine” “Conformal” “Projective” “Riemannian”)
Manifold-with-boundary 325 note 32
Marder, L. 296 368
Margenau, H. 293 367
Markus, L. 314 368
Marsden, J.E 305 325 351 360
Mascart, E.E.N. 293 368
Mass 9 107
Mass, inertial vs.gravitational 32 133 134 135 310 note note
Mass, longitudinal 13
Mass, proper 110
Mass, relativistic 112
Mass, transverse 113 307
Mass-energy equivalence 111 figure 306 note 308
Massey.G.J. 344 368
Matisse, Henri 203
Maximum signal speed 71 82 338
Maxwell equations 36 39 43 50 55 109 116 289 297 291 293 306 307 323 327
Maxwell, J.C. 36—38 39 49 117 130 288 289 290 293 308 368 369
McCarthy, P.J. 129 309 363
McCormmach, R. 290 291 314 369
McMullin, E 284 287 369
measured by Roemer 339 note 25
Mehlberg, H. 123 228 229 339 369
Mehra, J. 283 312 322 323 369
Meller, C. 293 295 315 345 370
Mercury’s perihelion precession 131 169 173 322
Merleau-Ponty, J. 289 294 325 369
Metric on a set (Grunbaum) 242
Metric space 303 note 1
Metric space, completion 211
Metrical amorphousness and continuity 242
Michell, J. 35
Michelson, A.A. 42 45 46 85 86 135 232 233 289 290 291 292 293 310 369
Microwave background radiation 204 255
Mie, G 138 142—143 175 195 312 313 322 369
Mignani, R. 296 372
Miller, A.I. 87 283 289 290 291 292 293 294 300 301 302 306 369
Miller, J.C 335 369
Milne, E A. 333
Minkowski metric 95
Minkowski metric, local approximation to global spacetime metric 150—152
Minkowski spacetime 90 92 95 186
Minkowski, H. 2 20 21 65 88—89 91 96 102 104 114 115 132 140 194 283 296 302—305 307—308 310 368 369
Minkowski’s world 89 303
mirf (momentary inertial rest frame) 96
Misner, C W. 215 255 284 312 317 325 330 332 335 337 344 347 352 369 370
Mittelstaedt, P. 297 306 339 363 370
Momentum, Newtonian 107
Momentum, relativistic 112
Mondrian, Piet 203
Monroe, C.J. 288
Morduch, G.E 310 312 378
More, H. 1
Morley, E W. 42 135 232 233 291 292 293 369
| Mortensen, C. 320 370
Motion 8
Motion, free vs.forced 30 96 158 194
Mukherjee, T.K. 297 355
Mukunda, N. 288 302 375
Munkres, J.R. 348 370
n-ad 6 99
n-ad field 6 99
n-ad field, holonomic 262
n-ad, orthonormal 279 303
n-ads, principal bundle of 264 figure
n-ads, principal bundle of canonic form 272
Narlikar, J.V. 284 317 331 332 364 370
Nerlich, G. 244 287 320 340 344 345 370
Neumann, C G. 3 12 16—17 286 370
Newman, ET. 330 335 370
Newton, I. 1 8—34 38 50 52 108 122 130 167 191 194 196 210 220 237 240 284—289 310 311 320 327 328 332 340 370
Newton’s programme for natural philosophy 8 35
Newton’s wisdom, as judged by Einstein 328 note 8
Nicomedes 1
Noble, H.R. 293 377
Nomizu, K. 284 295 313 314 317 335 348 349 366 370
Noonan, T.W. 289 295 373
Nordstrom, G 138 140—142 143 312 370
Normal chart 278
North, J.N. 325 371
Null cone in 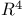 92 303 92 303
Null cone in Minkowski spacetime 92
Null curve 94
Null vector 92 94
Observationism, dismissed by Einstein (1933) 231
Observationism, dismissed by Einstein (1937) 331 note 39
Observationism, embraced by Einstein (1916) 328 note 4
Oersted, H.C. 35
Ohanian, H.C. 310 335 371
Ohrstrom, P. 337 371
Olbers, H.W.M. 332
Oppenheimer, J.R. 335 371
Orbit of an object under group action 295 note 14
Orthogonal (in Minkowski geometry) 91 figure
Orthonormal basis of inner product space 303 note 1
Ovchinnikova, V.V. 127 309 352
Ozswath, I. 331 371
O’Raifertaigh, L. 319 356 371
Panov, V.I. 310 353
Papapetrou, A. 323 324 355 371
Parallel cross-section 271
Parallel transport 101 187 270
Parallelism, in affine space 91
Parallelism, in principal fibre bundle 270
Parallelism, of vectors in affine manifold 187
Parallelism, path-dependent 187 f 266 270 326
Parallelizable manifold 93 99 265
PARAMETER 259
Parametric line of a coordinate function 259
Pargetter, R. 293 365
Parity 288 note 9 note
Pars, L.A. 298 299 371
Past directed causal curve 124
Past distinguishing spacetime 217
Past set 217
Path 6 94 259
Path topology 129
Pauli, W. 306 371
Peebles, P.J.E. 329 362 371
Pekar, D. 310 359
Penrose, R. 3 123 212 213 214 215 217 218 307 308 325 337 347 361 363 367 371
Penzias, A.A. 204 255 326 371
Pereira, C. 323
Permutation 24
Perrin, R.P. 296 371
Petrova, N.M. 324 371
Petzoldt, J. 314
Physical objects as geometrical objects 104
Pirani, F.A.E 4 193 202 296 319 325 327 331 343 344 353 356 371 377
pk (purely kinematic) coordinate transformation, Galilei 29
pk (purely kinematic) coordinate transformation, Lorentz 61 figure 65 295
Planck, M. 2 48 70 133 296 306 310 371 372
Poincare 283 note 4 340
Poincare group 6 62
Poincari, H. 1 2 3 83 84 85—87 114 132—133 283 288 291 292 296 300—302 303 305 310 340—341 343 350 372
Point transformation, Galilei 25
Point transformation, Lorentz 62
Poisson’s equation 33 34 133 159
Polnarev, A.G 325 362
Poston, T. 344 355
Pound, Ezra 203
Pound, R.V. 311 372
Power as inner product of velocity and relative force 113
Poynting vector 116 319
Priestley, J. 35
Principles of Chronology 82 300
Principles of Coexistence according to the Law of Interaction (Kant) 220
Principles of Conservation of 4-momentum 114
Principles of Constancy of Light Velocity (Light Principle) 49 54 55 67 84 138 293 294 3 295 311
Principles of Equivalence 19 32 134—138 151 195 287 310 311 note 3l5 316
Principles of Equivalence, allegedly generalizes Relativity Principle 134
Principles of Equivalence, but actually modifies it 136 figure
Principles of Equivalence, extended to arbitrary gravitational fields 151
Principles of Equivalence, “semi-strong” 311 note 13
Principles of Inertia 12 16 17 29 51 55
Principles of Reciprocity 79 298 note
Principles of Relativity (General) 153 195
Principles of Relativity (Newtonian) 19 30—31 39
Principles of Relativity (Special) 49 54 65 87 294 3 295 298
Principles of Relativity (Special), compared with General Relativity Principle 153 figure
Principles of Relativity (Special), modified by Equivalence Principle 136 figure
Principles of Relativity (Special), variously formulated by Poincare 83 85 301 note
Principles of Spatial Isotropy 79
Principles of Temporal Succession according to the Law of Causality (Kant) 221
Principles of Thermodynamics 49 83 “Mach’s
Projective structure of a manifold 191
Prokhovnik, S.J. 296 372
Proper time 96
Pseudo-group 316 note 6
Ptolemy 201
Pull-back 316 note 12
Putnam, H. 249 250 344 345 346 372
Pyenson, L. vi 302 310 372
Quadratic form 303 note 1
Quinn, P. 344 372
Radar chart 194
Radar signal 53
Raine, D.J. 199 202 332 372
Raychaidhuri, A.K. 200 213 332 372
Rayleigh, Lord (J.W.Strutt) 45 85 291 292 293 372
Recami, E. 296 372
Reciprocity 79
Reichenbach 234 figures (see also under “Simultaneity”)
Reichenbach “parameter” 223—225
Reichenbach “parameter”, truly a function 225—226
Reichenbach, H. 193 222 232—241 293 308 338—343 372
Reichenbach’s Rule for the definition of simultaneity 223 224 230 338 note 339
Reinhardt, M. 202 372
Relative force 112
Relativity, general 2 152—158 194 197 200 240 241
Relativity, General, dynamic formulation 181
Relativity, Newtonian vs. Einsteinian 38
Relativity, Newtonian vs. Einsteinian, incompatible with Newtonian gravity 131
Relativity, Newtonian vs. Einsteinian, locally valid only 136 figure
Relativity, Newtonian vs. Einsteinian, Special 2 48—82 85 107—121
Relativity, Newtonian vs. Einsteinian, transmutation of its laws into laws of General Relativity 156 figure 316
Repere 6 99
Repere, mobile 6 99
Ricci tensor 7 159 170 173 175 189 280 318
Ricci tensor, components 281 (D. 4)
Ricci tensor, Einstein’s notation of 196 321
Ricci-Curbastro, G. 2 102 143 146 326 373
Riemann tensor 145 189 279 280 313 318 note
Riemann tensor, components 281 (D. 2 D.
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



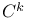 -differentiable
-differentiable