|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Torretti R. — Relativity and Geometry |
|
|
 |
| Предметный указатель |
Erlangen Programme 2 26 34 283 note 340
Essex, L. 292 378
Euclid 1 10 283 285 343
Euler, L. 286
Event 22
Expansion of the universe 203 330
Expansion of the universe, due to spacetime geometry 207
Exponential mapping 251 278
Exterior derivative 101 267
Faraday, M. 35 36 37 38 22 289 290 360
Feenberg, E. 293 360
Feinberg, G. 296 360
Fekete, E. 310 359
Fermat, P.de 334
Fermi chart 200 319
Fermi derivative 330 note 34’
Fermi transport 201 331
Fermi, E. 319 360
Fernparallelismus 191 327
Feynman, R.P. 309
Fibre 6 288
Fibre bundle, associated 264
Fibre bundle, principal 263
Field equations and equations of motion, in classical field theories 176
Field equations and equations of motion, in General Relativity 176 figures
Field, H. 288 360
Fine, A. 344 360
Fischer, A.E. 325 360
Fitzgerald — Lorentz contraction 45—46 85 292
Fitzgerald, G.F. 45 360
Fitzgerald, P. 296 360
Fizeau, A.H.L 42 289 291 360
Flat (in affine space) 91
Flat connection in principal fibre bundle 271
Flat linear connection 277
Flat Riemannian manifold or metric 145 280
Fock, V. 179 284 306 316 324 360
Fokker, A.D. 142 156 157 312 313 314 316 318 359 360
Foliation 345 note 47
Fomalont, E.B. 322 360
Force, differential (Reichenbach) 236
Force, impressed 8 284
Force, inertial 20 287
Force, innate 8 284 “Mass”)
Force, Newtonian 8 18 107
Force, Newtonian, represented by “same” vector relative to all inertial frames 19 107
Force, relativistic, Einstein’s definition of 1905 109 figure 112 306 307
Force, relativistic, Planck’s definition of 1906 112
Force, universal (Reichenbach) 236—238 342 note “Lorentz “Relative
Foucault’s pendulum 194 196
Four-acceleration 105 f 306
Four-current density 114
Four-force 114
Four-force density 115
Four-momentum 114
Four-potential, electromagnetic 307 note 3
Four-tensor field 102
Four-tensor field, meaningless relatively to arbitrary frames 106 154
Four-tensor field, ordinary tensor field uniquely defined by it 106 figure
Four-vector 86 102
Four-vector, decomposition into spacelike and timelike parts 104 305
Four-velocity 105 305
Fox, J.G. 293 360
Fox, R. 296 360
Frame 28
Frame, inertial 17—20 28 51 74 224 293
Frame, rigid 14 28
Frame, rotating 147—149 314 22 315 note
Frame, uniformly accelerated 310 note 6
Frame, “stationary” (Einstein, 1905d) 51 293
Frank, P. 296 298 360
Frederick Barbarossa 248 346
Freedom in scientific theorizing 56 231 340
French, A.P. 292 296 307 360
Fresnel, A.J. 38 41 42 43 45 70 360
Freudenthal, H. 288 360
Friedman, A. 326 360
Friedman, M. 21 339 344 356 360 361
Friedmann universes 204—210 212—213 219 333—334
Friedmann universes, dismissed by Einstein (1922) 204 333
Friedmann universes, embraced by Einstein (1931) 204 figure
Friedmann universes, periodic 335 note 9 337
Friedmann.Alexander 199 204—210 333—338 361
Friedmann’s equation 334 note 31
Friedmann’s hypotheses 205
Friedrichs, K. 287 361
Fubini, G. 206 333 361
Fung, Shing-Fai 339 361
Future directed causal curve 124
Future directed causal curve, vector 92
Future distinguishing spacetime 217
Future set 217
Galilei chart 23
Galilei chart, connection with inertial frames 29
Galilei group 26 65 288
Galilei invariants of Newtonian spacetime 27
Galilei, G. 22 31 49 287 288 361
Galison, P.L. 302 361
Gauss, C F. 1 144 146 149 257 313 314 347 361
Gauss’s Theorema egregium 144
General covariance 152—158 316 note 319 321
General covariance, judged impossible in gravitational theory by Einstein (1913/14) 163—165
General covariance, vindicated by Einstein (1915) 165—167
Geodesic deviation 343 note 38
Geodesic equations 151 (5 4 7*) 277
Geodesic incompleteness 212
Geodesic incompleteness, insufficient to characterize singular spacetimes 215 figure
Geodesic incompleteness, null-geodesic incomplete Lorentz metric conformal to a complete metric 336 note 10
Geodesic Law of Motion 151 315 316
Geodesic Law of Motion, implied under certain conditions by Einstein field equations 177 figures
Geodesic of linear connection 189 277
Geodesic, affine 187
Geodesic, complete 211 figure 278
Geodesic, Riemannian 94 304
Geometrical object 98 104 316
Geometry 1 2
Geometry and causality 123 255
Geometry and Gravitation 138 139 140 142 146 150—152 194—196 240 241 245
Geometry of Free Fall and Light Propagation 4 192—194 327
Geometry, elliptical 329 note 24
Geometry, Euclidean 89 285 286 4
Geometry, Euclidean, privileged according to Dingier 343 note 34
Geometry, Minkowski 89 figures 98 121
Geometry, Minkowski, characterized by causal structure 125—128
Geometry, Non-Euclidean of Minkowski spacetime 88 89
Geometry, Non-Euclidean of rotating frame 148 figure 315
Geometry, Non-Euclidean, Cayley — Klein theory 340 note
Geometry, Riemannian see “Riemannian manifold” “Riemannian
Geometry, spacetime 26figures 91—93 95—98 194
Geometry, “Riemann” (spherical) 329 note 23
Geroch, R.P. 216 217 254 325 335 336 337 347 361
Giannoni, C.B. 296 339 361
Giedymin, J. 350 361
Gillespie, C C. 289 361
global 257
Glymour, C. vi 284 311 320 322 323 344 347 356 361
Godel, K. 253 331 347 361 362
Goenner, H.F. 326 330 362
Goldberg, J.N. 179 180 324 363
Goldberg, S. 291 300 302 362
Goldenberg, H.M. 322
Gooding, D. 290 362
Gorini, V. 79 80 82 297 298 352
Gravitation, theories of, Abraham 139—140 312
Gravitation, theories of, Einstein — Grossmann 158—162 169 196
Gravitation, theories of, Einstein, 1913 outline 143 158
Gravitation, theories of, Einstein, 1915 final theory 173—175 237 322
Gravitation, theories of, Einstein, 1915 first theory 170—172
Gravitation, theories of, Einstein, 1915 second theory 172 figure
Gravitation, theories of, Einstein, main hypotheses 139 159 240 324
| Gravitation, theories of, Hilbert 175 figure
Gravitation, theories of, Lorentz 130f 310
Gravitation, theories of, Mie 142 figure 313 note 35 322
Gravitation, theories of, Minkowski 310 note 14
Gravitation, theories of, Newton 31—34 130 191 237
Gravitation, theories of, Nordstrom 140—142 312—313
Gravitation, theories of, Poincare 132—133 310
Gravitation, theories of, Reference to “Machian” theories 331 note 42
Gravitational energy and momentum 183 figure 319
Gravitational energy matrix 158 161 171
Gravitational energy matrix, called “energy tensor” (with sneer quotes) by Einstein 174
Gravitational field equations, (1917 version) 281 (D. 6); cf.
Gravitational field equations, (final 1915 version) 173 (5 7 17) 160 5 10)
Gravitational field equations, Einstein (discarded 1915 versions) 171 (5 7 4) 173 7 15)
Gravitational field equations, Einstein — Grossmann 161 (5 5 12) 319
Gravitational field equations, Poisson 33(1 7 4)
Gravitational field strength components in Einstein’s theories of gravity 151 158 189 237 317
Gravitational potential 7 33
Gravitational potential and spacetime metric 139 151
Gravitational potential and speed of light 138 140
Gravitational radiation 181 319 325 note
Gravitational radiation and equations of motion 181 figures
Gravitational radiation, propagation speed 181 310 note
Gravitational redshift 135 138 311 note
Gravity, as a universal force (Reichenbach) 236—238 342 note
Gravity, as a universal force (Reichenbach), linked to proper time 138 (see also “Geometry and gravitation”)
Green, G. 290 362
Greene, R.E. 326 362
Grishchuk, L.P. 325 362
Grommer, J. 178 197 323 324 359
Gron, O. 315 362
Grossmann, M. 139 142 143 146 152 158 159 161 162 163 169 176 312 314 315 316 318 319 320 321 322 324 328 359 362
Groth, E.J. 329 362
Groups, semidirect product of two 26 (see also “Action of a group” “Galilei “Lie “Lorentz “Poincare “Velocity
Grunbaum, A. vi 223 229 242—247 293 315 338 343 344—345 362
Guidance field (Fuhrungsfeld) 194
Guth, E. 283 362
Habicht, C. 48 292
Hafele, J.C 296 362
Hall, A.R. 284 285 286 320 362
Hall, D.B. 296 373
Hall, M.B. 284 285 286 320 362
Halley, E 332 362
Harrison, E.R. 332 363
Harvey, A.L. 310 363
Hausdorff topology 124 figure
Havas, P. vi 179 180 287 310 324 363
Hawking, S.W. 129 212 213 214 215 216 228 253 254 284 309 314 335 336 337 339 347 354 355 363 371
Heaviside, O. 38 290 293
Heintzmann, H. 306 363
Helmholtz, H.von 36 193 238 240 289 327 333 363
Herglotz, G. 88
Herivel, J. 288 363
Heriz, H. 38 39—40 42 50 130 289 290—291 293 363 364
Herneck, F. 319 363
Hessenberg, G 326 364
Hilbert, D. 88 175 232 285 302 308 320 321 323 364
Hill, A.R. 322 364
Hippias of Elis 1
Hirosige, T. 291 292 300 302 364
Hoek, M. 293 364
Hoffmann, B. 178 184 320 324 359 364 366 371
Hojman, S.A. 332 364
Hole argument against general covariance 163—168
Hole argument against general covariance, criticized by Hilbert 320 note 33
Holton, G. 292 293 300 364
Homeomorphism 348 note 2
Homogeneous space 72 296 6
Homotopic curves 346 note 11
Honl, H. 320 328 331 364
Horismos relation 121
Horismos, future 121
Horismos, past 121
Horizon, event 254 figure
Horizon, particle 254 figure
Horizon, Penrose particle 347 note 20
Horowitz, G.T. 254 336 347 361
Horwich, P. 344 364
Hoyle, F. 331 364
Hsieh, K.C. 339 361
Hubble, E 203 332 364
Humason, M.L. 203 364
Huygens, C. 33
Hypersurface 261
i-th coordinate function 14 256
i-th parametric line 259 (see also under “Fermi chart” “Galilei “Lorentz “Normal “Winnie
Ideal points of relativistic spacetime 183 216—218 324
Ignatowsky, W.von 3 76—82 298—299 364
Inertia 8 107 135
Inertia of charged particle moving in electromagnetic field 110
Inertia, compass of 200 330
Inertia, relative to masses, not “space” 197 (see also under “Mass”)
Inertial see under “Force” “Frame” “Mass” “Motion” “Time-scale”
Infeld, L. 178 179 184 323 324 359 364
Ingoli, F. 288
Inner product 303 note 1
Inner product, Minkowski (on 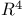 ) 91 ) 91
Integral curve of a vector field 260
Interval, Minkowski, in 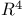 89 89
Interval, Minkowski, in 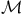 90 92 90 92
Invariant 26
Ives, H.I. 306 364
Iyanaga, S. 296 365
Jackson.F. 293 365
Jacobi’s equation 343 note 38
Jammer, M. 285 294 295 325 365
Janis, A.I. 315 338 362 365
Johnson, R. 217 365
Joyce, James 203
Kalotas, T.M. 298 367
Kamlah, A. 340 367
Kampen, E.R.van 316 374
Kanitscheider, B. vi 347 365
Kant, I.I. 221 222 228 231 232 233 234 288 289 340 341 365
Kaufmann.W. 290
Kawada, Y. 296 365
Keating, R.E 296 362
Kelvin, Lord (William Thomson) 38 290
Kepler, J. 203 332
Kernel of a linear mapping 349 note 2
Kerr, R.P. 253 335 365
Keswani, G H. 300 365
Kilmister, C.W. 291 293 294 295 301 302 306 310 311 315 316 323 328 365
King, A.R. 129 309 337 359 363
Klein, F. 2 26 34 176 283 329 330 340 341 365 366
Kobayashi, S. 284 295 313 314 317 335 348 349 366
Kohlrausch, F 37 289
Koslow, A. 287 366
Kottler, F. 306 316 366
Koyre, A. 285 366 370
Kramer, D. 347 366
Kretschmann, E 321 366
Kronheimer, E H. 3 123 217 308 337 361 366
Krotkov, R. 310 373
Kuchaf, K. 332 364
Lagrange, J.L. 38 288 366
Lanczos, C. 283 366
Landau, L.D. 287 293 345 366
Lange, L. 3 17—20 51 53 55 225 286 287 366
Langevin clock 52
Langevin, P. 52
Lansberg, A. 200
Laplace, P.S.de 310
Larmor, J. 290 292 296 366
Latzer, R.W. 308 309 366
Laub, J. 296 359
Laue, M.von 2 3 118—120 141 158 291 292 293 296 308 312 366 367
Lavoisier, A.L. 220
Law of Currents (Ampere) 35 36
Law of Gravity (Newton) 32 figures
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 )
)