Авторизация
Поиск по указателям
Frankel T. — The geometry of physics: an introduction
Обсудите книгу на научном форуме Нашли опечатку?
Название: The geometry of physics: an introductionАвтор: Frankel T. Аннотация: This book is intended to provide a working knowledge of those parts of exterior differential forms, differential geometry, algebraic and differential topology, Lie groups, vector bundles and Chern forms that are essential for a deeper understanding of both classical and modern physics and engineering. Included are discussions of analytical and fluid dynamics, electromagnetism, thermodynamics, the deformation tensors of elasticity, soap films, special and general relativity, the Dirac operator and spinors, and gauge fields, including Yang-Mills, the Aharonov-Bohm effect, Berry phase, and instanton winding numbers. Before discussing abstract notions of differential geometry, geometric intuition is developed through a rather extensive introduction to the study of surfaces in ordinary space; consequently, the book should also be of interest to mathematics students. This book will be useful to graduate and advanced undergraduate students of physics, engineering and mathematics. It can be used as a course text or for self study.
Язык: Рубрика: Физика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2001Количество страниц: 688Добавлена в каталог: 15.12.2013Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
67 200 200 88 (Cross) section 50 416 466 Absolute temperature 187 Acceleration, 4-vector 194 Accessibility 181 182 Accumulation point 106 action 152 274 524 Action, Euclidean 551 Action, first variation of 154 Action, group 454 Action, Hamilton's principle of stationary action 154 Action, Jacobi's principle of least action 281 Action, relativistic 196 AD 486 Ad, bundle 487 489 Ad, connection 487 Adiabatic distribution and leaf 183 Adiabatic process 180 Adjoint 392 640 Adjoint group 486 Adjoint representation 486 Admissible boundary form 378 Admittance matrix 645 Affine connection 242 Affine group of the line A(1) 394 Affine parameter 272 Aharonov — Bohm effect 447—448 554 Aharonov — Susskind and spinors 517 Algebra homomorphism 78 Ampere — Maxwell law 121 163 Annihilator subspace 167 Anticommutator 478 Antiderivation 89 135 antisymmetric 66 Associated bundle 482 Associated bundle, connection 483—487 Atiyah — Singer index theorem 465 Atlas 15 Bernoulli's theorem 234 Berry phase 468—472 Berry phase, equation 472 Bertrand — Puiseux and Diguet 288 Betti numbers 157 346 Bi-invariant connection on a Lie group 580 Bi-invariant forms on a Lie group 561 Bi-invariant Riemannian metric and their geodesics 563 Bianchi identities 300 489 Binormal 196 Bochner's theorems 374 530 Bonnet's theorem 229 Boundary (of a manifold) = edge 106 Boundary conditions, essential or imposed 527 Boundary conditions, natural 527 Boundary group 344 Boundary homomorphism 338 601 Boundary operator 335 637 Bracket, anticommutator 478 Bracket, commutator 408 Bracket, Lagrange 80 100 Bracket, Lie 126 402 Bracket, Lie of g-valued forms 477 Bracket, Poisson 154 Brillouin and the stress form 635 Brouwer degree 210—213 360 Brouwer degree, fixed point theorem 217 Bump form 107 Bundle space 415 Bundle, associated 482 Bundle, complex line 433 Bundle, cotangent 52 Bundle, determinant 487 Bundle, dual 482 Bundle, electromagnetic 441 Bundle, fiber 415 Bundle, frame 453 Bundle, gauge 490 Bundle, line 433 Bundle, local trivialization 417 Bundle, monopole 444 473 Bundle, normal 419 Bundle, orientable 611 Bundle, principal 454 481 Bundle, product 418 Bundle, projection 415 Bundle, pull back 622 Bundle, section 50 416 466 Bundle, structure group 433 452 Bundle, tangent 48 Bundle, transition functions 24 254 414 Bundle, trivial 418 Bundle, unit tangent 51 Bundle, vector 413—417 Bundle, volume 488 Canonical form 394 Canonical map 149 Caratheodory's formulation of the second law of thermodynamics 181 Caratheodory's theorem 182 Cartan's 3-form on a Lie group 566 Cartan's bi-invariant forms 562 Cartan's exterior covariant differential 250 430 Cartan's method for computing curvature 257 Cartan's structural equations 249 Cartan's theorem 606 Cauchy equations of motion 618 620 628 Cauchy stress form 619 Cauchy stress form, Lie derivative of 634 635 Cauchy stress form, symmetry of 621 Cauchy — Green tensor 82 Cauchy — Riemann equations 158 159 Center of a Lie algebra 580 Center of a Lie group 565 Chain complex 636 Chain group 337 Chain group, integer 336 Chain group, simplicial 343 Chain group, singular 333 Characteristic cohomology class 616 Charge form 118 Chern — Simons form 586 Chern — Weil theorem 589 Chern's forms and classes 587—591 Chern's forms and classes as obstructions 608—616 Chern's integral 612 Chern's proof of Gauss — Bonnet — Poincare 462—465 553—557 Chern's theorem 615 Chow's theorem 178 187 Christoffel symbols 229 Circulation 144 377 Clairaut's relation 530 Classical force 195 Classical momentum 194 Classical velocity 193 Clifford algebra 500 Clifford embedding 262 Clifford numbers 503 Closed form 156 158 Closed manifold 120 Closed set 11 Closure 106 Coboundary 638 Cochain 638 Coclosed 370 Cocycle 639 Codazzi equation 229 302 311—313 320 Codifferential d* 364 Codimension 6 Coefficient group 337 Coefficient group, field 343 Cohomology 356 Cohomology 615 Commutative diagram 338 Commutator bracket of matrices 408 Compact 13 Completable relative cycle 387 Complex analytic map 158 214 Complex line bundle 433 Complex line bundle, connections 434 Complex manifold 21 Composing rotations 499 Configuration space 9 50 Conformally related metrics 531 Conjugate point 327 Connected space 347 Connection 242 Connection on a Lie group 580 Connection on a Lie group, flat 581 Connection on a vector bundle 428—431 Connection on the associated Ad bundle 486 Connection, coefficients of 243 429 Connection, curvature of 244 Connection, electromagnetic 440 Connection, flat 260 Connection, forms 249 256 Connection, forms 462 480 Connection, induced 309 Connection, Levi-Civita or Riemannian 242 245 Connection, Simon 472 Connection, spinor 518—521 Connection, symmetric 245 Connection, torsion of 245 Connection, torsion-free 245 Constraint, holonomic 175 Constraint, nonholonomic 175 continuous 12 Continuum mechanics 617—635 Continuum mechanics, equilibrium equations 630 Contractible to a point 161 Contraction 89 Contravariant tensor 59 Contravariant vector 23 Coordinate, change of 29 Coordinate, compatible 15 Coordinate, frame 243 Coordinate, homogeneous 17 Coordinate, inertial 192 Coordinate, local 3 4 13 Coordinate, map 20 Coordinate, patch 20 Coset space G/H 456 Coset space G/H, fundamental principle 457 Cotangent space 40 Coupling constant or charge 539 Covariance 430 Covariant components of a tangent vector 43 Covariant constant 267 Covariant derivative 235 241—244 430 Covariant derivative 298—299 Covariant derivative 301 Covariant differential 248 Covariant tensor 58 Covariant vector = covector 41 Covector 41 Covector, transformation law 42 Covering space 569—576 Covering space, associated to a subgroup of 575 Covering space, orientable 573 Covering space, universal 570 Covering space, universal, covering group 575 Critical points and values 28 382—387 Critical points and values, homotopically 382 387 Critical points and values, index 384 Critical points and values, inessential 383 Critical points and values, nondegenerate 383 Curl 93 Current 2-form j 118 Current 3-form 199 Current 3-vector 119 Current 4-vector J 199 Current convective 119 Current electric, as a chain 644 Curvature and parallel displacement 259—261 Curvature of a connection 243 Curvature of a space curve 191 Curvature of a surface 207 Curvature of a surface of revolution 258 Curvature of the Poincare metric 258 Curvature, extrinsic 318 Curvature, forms 251 256 431 Curvature, forms 489 Curvature, forms 257 Curvature, forms 462 Curvature, forms 481 Curvature, Gauss 207 Curvature, geodesic 235 Curvature, intrinsic 318 Curvature, mean 207 Curvature, principal 207 Curvature, Riemann sectional K( 313 Curvature, Riemann tensor 244 Curvature, total 215 Curvature, transformation R(X, Y) 244 Curvature, vector 192 194 Cycle, absolute 344 Cycle, completeable 387 Cycle, group 344 Cycle, relative 379 D'Alembertian 293 371 de Rham's theorem 355—360 de Rham's vector space 356 Deformation retract 406 506 Deformation tensor 82 Deformation Theorem 350 Degree of a map see "Brouwer degree" Derivation 134 Derivative, covariant 235 Derivative, exterior 73 Derivative, intrinsic 235 Derivative, normal 364 Determinant line bundle 487 Dictionary relating forms and vectors 94 Diffeomorphism 27 Differentiable 20 Differential form see "Form" Differential of a function 40 Differential of a map 7 27 Differential, exterior d 73 Differential, exterior d, covariant 250 Differentiation of integrals 138—143 Dirac (4-component) spinor 513 Dirac adjoint or conjugate spinor 532 Dirac algebra 509 Dirac equation 503 Dirac Lagrangian 531 Dirac matrices 510 Dirac monopole 444 Dirac monopole, quantization 445 Dirac operator 511 514 521 Dirac operator in curved space 515—521 Dirac program 502 Dirac representation 512 Dirac string 162 Dirichlet's principle 373 Distance from a point to a hypersurface 579 Distribution (of subspaces) 166 Distribution (of subspaces), adiabatic 183 Distribution (of subspaces), horizontal 263 Distribution (of subspaces), integrable 167
Реклама
 |
|
О проекте
|
|
О проекте



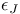
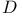
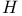
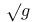
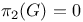
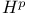

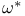 in the frame bundle
in the frame bundle 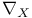
 , exterior
, exterior 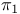
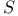
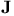

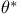 on a frame bundle
on a frame bundle 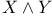 )
)