Авторизация
Поиск по указателям
Frankel T. — The geometry of physics: an introduction
Обсудите книгу на научном форуме Нашли опечатку?
Название: The geometry of physics: an introductionАвтор: Frankel T. Аннотация: This book is intended to provide a working knowledge of those parts of exterior differential forms, differential geometry, algebraic and differential topology, Lie groups, vector bundles and Chern forms that are essential for a deeper understanding of both classical and modern physics and engineering. Included are discussions of analytical and fluid dynamics, electromagnetism, thermodynamics, the deformation tensors of elasticity, soap films, special and general relativity, the Dirac operator and spinors, and gauge fields, including Yang-Mills, the Aharonov-Bohm effect, Berry phase, and instanton winding numbers. Before discussing abstract notions of differential geometry, geometric intuition is developed through a rather extensive introduction to the study of surfaces in ordinary space; consequently, the book should also be of interest to mathematics students. This book will be useful to graduate and advanced undergraduate students of physics, engineering and mathematics. It can be used as a course text or for self study.
Язык: Рубрика: Физика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2001Количество страниц: 688Добавлена в каталог: 15.12.2013Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Killing field, equation 529 Kinetic term 535 Kirchhoff's current law (KCL) 644 Kirchhoff's voltage law (KVL) 644 Klein bottle 348 Klein — Gordon equation 502 Kronecker delta, generalized 67 Kronecker index of a vector field 216 Lagrange bracket { , } 80 100 Lagrange deformation tensor 82 625 Lagrange's equations 147 Lagrange's equations in a curved 276 Lagrange's equations with electromagnetism 439 Lagrange's equations, tensorial nature 526 Lagrangian 54 Lagrangian for particle in an electromagnetic field 436—439 Lagrangian, Dirac 531 Lagrangian, electromagnetic 308 Lagrangian, significance in special relativity 437 Lambert's formula 290 Laplace operator 368—372 Laplace operator 370 Laplace operator on a cochain 641 Laplace's formula for pressure in a bubble 227 Laplacian 93 305 Laplacian 305 Leaf of a foliation 173 Leaf of a foliation, maximal 173 Levi-Civita connection 242 Levi-Civita equation 297 Levi-Civita parallel displacement 237 Lie algebra g 402 Lie algebra g, Ad invariant scalar product 543 Lie bracket [ , ] 126 402 Lie derivative 132—138 Lie derivative 125 Lie derivative 625 Lie derivative 634 635 Lie group 391—412 Lie group, 1-parameter subgroup 398 405—407 564 Lie group, 1-parameter subgroup on Sl(2, 407 Lie group, compact 541 Lie group, compact, averaging over 541 Lie group, compact, bi-invariant forms 561—567 Lie group, connection and curvature of 580 Lie subgroup and subalgebra 410—412 Lifting paths 277 Lifting paths in a bundle 593 Lifting paths in a covering space 574 Lifting spheres 605 Light cone 193 Lightlike 193 Linear functional 38 Linking number 219 Liouville's theorem 148 Local product 49 Local trivialization 417 Lorentz factor 193 Lorentz force 119 Lorentz force, covector 120 197 Lorentz group 504 Lorentz group and spinor representation of Sl(2, 509 Lorentz metric 192 Lorentz transformation 46 198 Magnetic field 119 Magnetic field 123 387 Magnetic field 121 Magnetic field 120 Magnetohydrodynamics 145 Manifold 13 19 Manifold with boundary 106 Manifold, closed 120 Manifold, complex 21 Manifold, integral 166 Manifold, mechanical 180 Manifold, orientable 83 Manifold, product 15 Manifold, pseudo-Riemannian 45 Manifold, Riemannian 45 Manifold, symplectic 146 Map of manifolds: critical points and values 28 Map of manifolds: regular points and values 28 Map, canonical 149 Map, coordinate 20 Map, differentiable 20 Map, exponential 284 399 Map, geographical 230 Map, inclusion 79 Map, projection 415 Matrix group 394 Maurer — Cartan equations 403 477 Maurer — Cartan form 476 Maximal atlas 15 Maximal torus 393 Maxwell's equations 120—123 198 200 536 Maxwell's equations on a 3-sphere 163 Maxwell's equations on a curved space 366—367 Maxwell's equations on a torus 122 Maxwell's equations on projective space 164 Maxwell's equations, independence of 200 Mayer — Lie system 174 Mean curvature 207 311 529 Mean curvature and divergence 224 Mesons 538 Mesons, Yukawa 540 Metric, conformally related 531 Metric, flat or locally euclidean 263 Metric, Lorentz or Minkowski 192 Metric, potentials 293 Metric, pseudo-Riemannian 45 Metric, Riemannian 45 Metric, spatial 297 Metric, static 292 296 Metric, stationary 291 Metric, tensor 43 Minimal submanifold 311 528 Minimal submanifold, surface 227 305 Minimization of arc length 286 Minkowski electromagnetic field tensor 197 Minkowski force 195 Minkowski metric and space 46 192 Mode, normal 65 Mode, zero 465 Moebius band 18 Momentum, 4-vector 194 Momentum, canonical 439 Momentum, classical 194 Momentum, density 320 322 Momentum, generalized 55 Momentum, kinematical 436 Momentum, operator 439 Monopole bundle 444 473 Morse deformation 47 Morse equalities 387 428 Morse index 328 384 Morse inequalities 385 386 Morse lacunary principle 388 Morse lemma 384 Morse polynomial 385 Morse theory 382—388 Morse type number 385 604 Multilinear 58 Myers's theorem 576—578 Neighborhood 12 Noether's theorem 527—529 Nomizu's theorem 530 Normal bundle 419 616 Normal coordinates 287 303 Normal derivative 364 Normal map 208 Normal mode 65 Nucleon, Heisenberg 537 Nucleon, Yang — Mills 538 Obstruction cocycle 609—612 One parameter group 31 Open set 11 12 Orientability 83 Orientability and curvature 331 Orientability and homology 349 Orientability and two-sidedness 84 Orientable bundle 611 Orientable manifold 83 Orientable transverse 115 Orientation 82 Orientation of the boundary 110 Orientation, coherent 341 Orientation, transverse 115 Orthogonal group, O(n) 9 392 Orthogonal group, SO(n) 9 392 Osculating plane 191 Paper folding 315 Parallel displacement 237 Parallel displacement, independence of path 260 Parallelizable 252 Parameter, distinguished or affine 272 Parameterized subset 97 Partition of unity 107 Partition of unity and Riemannian metrics 109 Passes peaks and pits 427 Path ordering 555 Pauli algebra 501 Pauli matrices 493 Period of a form 357 Periodic motion 282 Periodic motion for double pendulum 284 Periodic motion for rigid body 331 Pfaffian 167 Phase 448 535 Phase, space 55 Phase, space, extended 151 Physical components 48 630 Piola — Kirchhoff stress forms, first 622 Piola — Kirchhoff stress forms, second 623 Poincare 1-form 56 Poincare 1-form, extended 151 Poincare 2-form 80 Poincare 2-form, extended 151 437 Poincare characteristic 604 Poincare duality 375 Poincare Index Theorem 421—428 Poincare lemma and converse 160 Poincare metric 239 258 Poincare metric, geodesics 274 530 Poincare polynomial 385 Poisson bracket ( , ) 154 Poisson equation 293 371 Potential of a closed form 158 160—164 Potential, global vector 443 448 Potential, monopole 444 Potential, singularities see "Dirac string" Poynting vector 322 Principal bundle 454 458 481 Principal directions 207 310 Principal normal 191 Principal normal curvatures 207 310 Principle of least action 281 Probability amplitude 447 Projection 49 415 Projection, homomorphism 605 Projective space 16 85 Projective space, 22 Projective space, 16 Projective space, homogeneous coordinates 17 Proper time 193 292 Pseudo-form 86 Pseudo-riemannian 45 Pseudoform 86 Pseudoform, integration of 114—417 Pull-back and integration 102 Pull-back in elasticity 81 622 Pull-back of covariant tensors 53 77 79 Pull-back, bundle 622 Pure gauge 553 Quantization of a gauge field 536 Quantization of a gauge field, topological 261 Quark 540 Quasi-static 179 Quaternion 502 Quotient group 345 Radius of curvature 192 221 Rate of deformation tensor 632—634 Regular points and values 28 Relative boundaries, cycles, and homology groups 379—381 Relative homology sequence 604 Relativistic equations of mass 194 Relativistic equations of motion 303 Reparameterization 101 Representation 481 Representation of a group 481 482 Representation, adjoint, Ad 486 Representation, dual 482 Representation, tensor product 482 Residue of a form 159 Rest mass 194 Retraction 217 Ricci curvature 315 374 577 Ricci identities 302 Ricci tensor 295 Riemann sectional curvature K( 313—314 Riemann sphere 21 Riemann Theorem 266 Riemann — Christoffel curvature tensor 229 Riemannian connection 242 Riemannian manifold and metric 45 Riemannian manifold and metric on a surface of revolution 258 Riemannian manifold and metric, bi-invariant 563 Rigid body 9 331 Rotation group SO(n) 392 492 Sard's theorem 29 Scalar curvature R 296 Scalar product 42 Scalar product of Hermitian matrices 494 Scalar product, global 361 Scalar product, nondegenerate 42 Schroedinger's equation 439 Schroedinger's equation in curved space 442 Schroedinger's equation with an electromagnetic field 440 443 Schwarz's formula 228 Schwarzschild solution 320—322 Section 50 416 466 Section, holomorphic 467 Section, p-form section of a vector bundle 488 Sectional curvature 313 Self (anti) dual field 549 Self adjoint 205 317 Serret — Frenet formulas 196 431 Simon connection 472 simplex 333 Simplex, boundary 335 Simplex, face 335 Simplex, ordered 335 Simplex, orientation 336 Simplex, singular 334 Simplex, standard 333 Simplicial complex 343 Simply connected 283 329 595 Singularity of a vector field 422 Skeleton 610 Smooth 7 Soap bubbles and films 226—228
Реклама
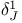
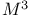
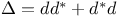on forms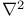 
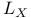of a form 
) 
) 
) 
|
|
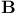
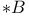
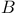
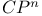
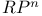
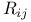
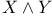О проекте