Авторизация
Поиск по указателям
Frankel T. — The geometry of physics: an introduction
Обсудите книгу на научном форуме Нашли опечатку?
Название: The geometry of physics: an introductionАвтор: Frankel T. Аннотация: This book is intended to provide a working knowledge of those parts of exterior differential forms, differential geometry, algebraic and differential topology, Lie groups, vector bundles and Chern forms that are essential for a deeper understanding of both classical and modern physics and engineering. Included are discussions of analytical and fluid dynamics, electromagnetism, thermodynamics, the deformation tensors of elasticity, soap films, special and general relativity, the Dirac operator and spinors, and gauge fields, including Yang-Mills, the Aharonov-Bohm effect, Berry phase, and instanton winding numbers. Before discussing abstract notions of differential geometry, geometric intuition is developed through a rather extensive introduction to the study of surfaces in ordinary space; consequently, the book should also be of interest to mathematics students. This book will be useful to graduate and advanced undergraduate students of physics, engineering and mathematics. It can be used as a course text or for self study.
Язык: Рубрика: Физика /Статус предметного указателя: Готов указатель с номерами страниц ed2k: ed2k stats Год издания: 2001Количество страниц: 688Добавлена в каталог: 15.12.2013Операции: Положить на полку |
Скопировать ссылку для форума | Скопировать ID
Предметный указатель
Divergence 93 136 304 Divergence of a form 365 Divergence of a symmetric tensor 300 Divergence theorem 139 Divergence, exterior covariant 545 Dual basis 39 Dual bundle 417 482 Dual Hodge * 362 Dual space 39 Eigenvalue of a quadratic form 63 209 Einstein equations 296 316 317 Einstein equations, Wheeler's version 318 Einstein geodesic assumption 292 297 Einstein tensor G 315 Electric field 119 Electric field 123 378 381 Electric field 120 Electric field 121 Electromagnetic bundle 441 Electromagnetic connection 440 Electromagnetic field strength 197 Electromagnetic Lagrangian 308 Electromagnetic stress-energy-momentum tensor 308 Electromagnetic vector potential 1-form 199 Electromagnetism and Maxwell's equations in curved spacetime 366—367 Electromagnetism and Maxwell's equations on projective space 164 Electromagnetism and Maxwell's equations on the 3-sphere 163 Electromagnetism and Maxwell's equations on the 3-torus 122 Electromagnetism and Maxwell's equations, existence and uniqueness 378 387 Embedded submanifold 27 Energy of a path 274 Energy of deformation 623—626 Energy, density 316 Energy, hypersurface 148 Energy, hypersurface, invariant form 150 Energy, internal 179 Energy, momentum tensor 295 Energy, momentum vector 195 Energy, rest 195 Energy, total 148 196 entropy 183 Entropy, empirical 185 Equations of motion 144 Equations of motion, relativistic 303 Equilibrium equations 630—632 Euclidean metric in quantum fields 551 Euler characteristic 423 426 Euler equations of fluid flow 144 Euler integrability condition 166 Euler principle of least action 281 Exact form 156 Exact sequence 598—600 Exact sequence, homology 604 Exact sequence, homotopy 600 Exact sequence, short 599 EXP 284 Exponential map for a Lie group 399 403 Extension theorem 592 Exterior algebra 68 Exterior covariant differential 250 430 Exterior covariant differential 488 Exterior covariant divergence 545 Exterior differential d 73 Exterior differential d, coordinate expression 76 Exterior differential d, spatial d 141 Exterior form 66 Exterior form and vector analysis 71 Exterior power operation 588 Exterior product 67 Exterior product and determinants 71 Exterior product, geometric meaning 70 Face 335 Faraday's law 121 Fermat's principle 297 Fiber 49 415 Fiber bundle 451 594 Fiber coordinate 416 Fiber over p 416 Fiber space 593 Field strength 64 Flamm paraboloid 321 Flow generated by a vector field 32 33 Flow generated by invariant fields 408 Flow generated by Lie bracket 129 Flow, straightened 35 Fluid flow 30 143—145 Fluid flow, magnetohydrodynamic 145 Foliation 173 Force, classical 195 Force, Lorentz 119 Force, Minkowski 195 Form and pseudo-form 122 Form of type Ad 489 490 Form with values in a Lie algebra 475 477 Form, bi-invariant 561—563 Form, Cartan 562 Form, Cauchy stress form 618 Form, closed 156 Form, exact 156 Form, exterior 66 Form, first fundamental 202 Form, harmonic 370 Form, heat 1-form 179 Form, integration of 95—102 Form, integration of and pull-backs 102 Form, invariant 395 Form, Maurer — Cartan 476 Form, normal 376 Form, p-form 41 Form, pull-back 77—82 Form, second fundamental 204 309 Form, second fundamental and expansion of the universe 318 319 Form, stress: Cauchy 618 Form, stress: Piola — Kirchhoff 622 623 Form, tangential 376 Form, vector bundle-valued 429 Form, vector-valued, dr and dS 203 248 Form, volume 86 88 Form, work 1-form 179 Frame bundle 453 Frame e 243 Frame e of sections 417 Frame e, change of 253 Frame e, coordinate 243 Frame e, orthonormal 255 Frobenius chart 167 Frobenius theorem 170 Functional derivative 307 Fundamental group 567—569 578 Fundamental theorem of algebra 215 Fundamental vector field 455 Galloway's theorem 578 Gauge bundle 490 Gauge field 255 536 Gauge invariance 441 449 533—536 Gauge particles: gluons 540 Gauge particles:mesons 538 Gauge particles:photons 536 Gauge principle 537 Gauge transformation 255 490 Gauge transformation, global 535 Gauss curvature 207 Gauss equations 229 310 311—314 Gauss equations, relativistic meaning 316—318 Gauss formula for variation of area 225 Gauss law 121 Gauss lemma 286 Gauss linking or looping integral 218 Gauss normal map 208 215 260 Gauss theorema egregium 231 317—318 Gauss — Bonnet theorem 215 323 462 Gauss — Bonnet theorem as an index theorem 465 Gauss — Bonnet theorem, generalized 465—468 Gaussian coordinates 284 Gell-Mann matrices 540 General linear group GL(n) 254 391 General relativity 291—322 Generalized momentum 55 Generalized velocity 50 Geodesic 233 271—274 Geodesic in a bi-invariant metric 563 Geodesic, circle 287 Geodesic, closed 281 284 Geodesic, completeness 564 Geodesic, curvature 235 239 Geodesic, equation 235 Geodesic, J. Bernoulli's theorem 234 Geodesic, null 303 Geodesic, polar coordinates 287 Geodesic, stability 324 326 Geodesic, submanifold 310 Geodesic, submanifold, total 311 Geodesy 252 Gluons 540 Gradient vector 45 Grassmann algebra see also "Exterior algebra" Grassmann algebra, manifold 459 Green's reciprocity 647 Green's theorem 368 Group, 336 Group, boundary 344 Group, chain 337 Group, cycle 344 Group, de Rham 356 Group, exact sequence 598 Group, homology 345 Group, homomorphism 337 398 Group, homotopy 596 Group, quotient 345 H. Cartan's formula 135 Haar measure 397 541 Hadamard's lemma 126 Hairy sphere 423 Hamilton's equations 147 Hamilton's principle 154 275 Hamilton's principle in elasticity 626—629 Hamilton, on composing rotations 499 Hamiltonian 147 Hamiltonian flow 148 Hamiltonian operator 439 Hamiltonian relativistic 196 Hamiltonian vector field 148 Harmonic cochain 641 Harmonic field 376 Harmonic form 370 Harmonic form in a bi-invariant metric 564 Hawking singularity theorem 579 Heat 1-form 179 Helicity 145 Helmholtz decomposition 372 Hermitian adjoint t 392 Hermitian line bundle 466 Hessian matrix 383 Hilbert action principle 308 Hilbert space inner product 361 Hilbert variational approach 305—308 368 Hodge 362 Hodge codifferential d* 364 Hodge decomposition 372 388 Hodge theorem 371 Hodge theorem for normal forms 381 Hodge theorem for tangential forms 377 Holomorphic 158 Holonomic constraint 175 Holonomy 259 Homeomorphism 13 Homogeneous space 458 Homologous 345 Homology group 345—355 Homology group, relative 379 Homology group, relative, sequence 604 Homomorphism 337 398 Homomorphism, algebra 78 Homomorphism, boundary 338 601 Homomorphism, induced 337 Homotopically critical point 382 Homotopy 591 Homotopy and homology 603 Homotopy groups 596—598 Homotopy groups 605 Homotopy groups 597 598 Homotopy groups 605—608 Homotopy, covering homotopy 592 Homotopy, free homotopy class 282 283 Homotopy, sequence for a bundle 600—603 Hopf bundle 473 474 Hopf map and fibering 606 Hopf theorem 427 Hopf — Rinow theorem 564 Horizontal distribution 263—266 481 Hurewicz Theorem 603 Hyperelastic 626 Hypersurface 6 Hypersurface, 1- and 2-sided 84 Hypersurface, parallel 286 Immersion 169 173 Implicit function theorem 5 Incidence matrix 645 Inclusion map 79 Index of a section 466 Index of a vector field see also "Kronecker index" Index theorem 465 Indicator 315 Infinitesimal generator 399 Instanton 550 Instanton, winding number 556 560 Integrability condition 166 170 174 Integrable constraint 175 Integrable distribution 167 Integral curve 31 Integral manifold 166 Integrating factor 183 Integration of forms 96—109 Integration of pseudoforms 114—117 Integration over manifolds 104—109 Interaction 534 Interior product 89 Intersection number 219 INTRINSIC 234 Intrinsic, derivative 235 Invariant form 395 Invariant vector field 395 Invariant volume form 397 Inverse function theorem 29 Inverse image 12 Involution 167 Isometry 230 314 Isometry, fixed set 314 Isometry, invariant 231 Isotropy subgroup 457 j 432 Jacobi determinant 5 Jacobi equation of geodesic variation 273 Jacobi field 129 273 326—329 Jacobi identity 403 Jacobi metric 281 Jacobi principle of least action 281 Jacobi rule for change of variables in an integral 101 Jacobi variational equation 128 Killing field 528
Реклама
, 
, 
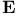
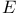
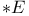
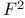
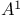
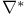
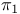
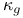
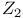
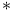operator 
|
|
О проекте