|
|
 |
| Авторизация |
|
|
 |
| Поиск по указателям |
|
 |
|
 |
|
|
 |
 |
|
 |
|
| Hille E. — Methods in classical and functional analysis |
|
|
 |
| Предметный указатель |
Space, characteristic = eigen 37
Space, complex Euclidean 1-50
Space, conjugate 88 137 221
Space, Euclidean three space 1-13
Space, Hausdorff 218
Space, Hilbert 69-80
Space, inner-product 67-80 331-361
Space, linear operator 63-67 305-330
Space, linear vector 51-84
Space, measurable 113
Space, measure 113
Space, metric 39-41 54-55 159-188
Space, null 14
Space, pre — Hilbert 67
Space, reflexive = regular 221
Space, root 36
Space, second dual 221
Space, structure 51
spaces 51-56
Spectral mapping theorem 296 302 354-361
Spectral properties 328
Spectral theorem 354-361
Spectrum 277 279
Spectrum, continuous 328
Spectrum, point 183 328
Spectrum, residual 328
Steinhaus theorem 308
Stieltjes integral 146 469
Stoll, R. R. 50
Stone, M. H. 341 361
Structure, algebraic 51
Structure, metric 51 189
Structure, topological 217
Subadditive functions 380-399
Subadditivity 12 40 380-400
Suboperative functions 385
Successive approximations 194 204
Successor 85
Summability 449-451
Summability, Ces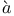 ro 95 185 ro 95 185
Summability, Fej r 152 157 r 152 157
Summability, Lebesgue 158
Supremum 163
Supremum, essential 137
Surjection, surjective = onto 15
System orthogonal, orthonormal 12 69-73
Szeg logarithmic capacity 473 logarithmic capacity 473
Szeg transflnite diameters 456 457 471 transflnite diameters 456 457 471
Szeg , G. 456 468 , G. 456 468
Szekeres, G. 172
Tangential coordinates 395
Targonski — Bourlet operators 424 426
Targonski, G. I. 424 426 435
Taylor expansion 167 255
Taylor, A. E. 84 249 264
Theorem, Acz l 427 l 427
Theorem, Acz l — Hossz l — Hossz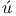 430 436 430 436
Theorem, Acz l — Ng 430-433 l — Ng 430-433
Theorem, addition 376 424 435
Theorem, Arzel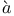 98 151 98 151
Theorem, Banach fixed point 169-172
Theorem, Banach — Steinhaus 308
Theorem, Bernstein 101
Theorem, Bohnenblust — Sobezyk 319
Theorem, Bolshoff — Kellogg 159
Theorem, Bolzano — Weierstrass 98 160
Theorem, Brouwer 159
Theorem, Carlson — Cram r — Wigert 264 r — Wigert 264
Theorem, Cayley — Hamilton 34
Theorem, closed graph 312
Theorem, consistency 450
Theorem, dominated convergence 136 240
Theorem, Fej r 157 r 157
Theorem, Fubini 135 469
Theorem, Gelfand, representation 290-296
Theorem, Gelfand, uniqueness 300
Theorem, Hahn — Banach 318
Theorem, Heine — Borel 160
Theorem, identity 255
Theorem, implicit function 189-194
| Theorem, Jordan 253
Theorem, Landau — Kallman — Rota 167 183 361
Theorem, Lebesgue approximation -s 100 158
Theorem, Liouville 257
Theorem, monodromy 263
Theorem, monotone convergence 238
Theorem, Morera 258
Theorem, Nagumo -s 285 326 366 378
Theorem, Ng 430 433
Theorem, Phragm n — Lindel n — Lindel f 263 f 263
Theorem, positive operator 345-346
Theorem, Pythagoras 69 332
Theorem, Runge 258
Theorem, Spectral 354-361
Theorem, Spectral Mapping 296 302 354-361
Theorem, Splitting 349 350
Theorem, Toeplitz — Hausdorff 356-341
Theorem, uniform boundedness 217
Theorem, Vitali — Lindel f 258-264 272-274 f 258-264 272-274
Theorem, Weierstrass approximation 99
Thomas, L. M., — Fermi equation 416
Toeplitz — Hausdorff theorem 335-341
Toeplitz, O. 335 361
topologies 217-226
Topologies, Hausdorff 218
Topologies, strong 217
Topologies, weak 218 220
Torus 172
Transformation see also Linear transformation mapping
Transformation, bounded linear 56-60 63-66 305-310
Transformation, bounded linear, one-parameter semi-group 167
Transformation, bounded non-linear 165
Transformation, bounded non-linear, semi-group 165
Transformation, closed 307 310-316
Transformation, Fourier 360
Transformation, Picard 169
Transformation, Poisson 172
Translation-invariant 448
Truncation 123
Uniform boundedness principle 212-217
Uniqueness theorems for differential equations 365-366
Uniqueness theorems for fixed points 169-179
Uniqueness theorems for functional equations 426-436
Unit element 21 86 277
Unit matrix 21
Unit of length 1
Unit operator = identity 65
Unit sphere 13
Unit vector 2
Valuations, non — Euclidean 409-410 461
Vector 1 9 51
Vector space 52
Vector, addition 2 8 52
Vector, negative of 52
Vector, negative, positive 1
Vector, positive 164
Vincze, E. 426 436
Vitali theorem 258-264 272-274
Vitali, G. 258
Volterra fixed point theorem 176-177
Volterra inequality 369
Volterra integral equations 179-181
Volterra, V. 176
Walter, W. 379
Waring, E., — Newton-formula 473
Wedderburn, J. H. Maclagan 25
Wedderburn, J. H. Maclagan, matrix norm 25
Weierstrass algebraic addition theorems 424
Weierstrass approximation theorem 99
Weierstrass — Bolzano theorem 98
Weierstrass, K. 99 179
Weyl, H. 342
Wiener, N. 249
Wigert, S. 264
Wong, E. T. 50
Yood, B. 15
Yosida, K. 167 187
Zermelo, E., Zermelo axiom of choice 163
Zorn (F)-differentiability 269
Zorn lemma, maximal principle 163
Zorn, M. 163 264
|
|
 |
| Реклама |
 |
|
|
 |
|
О проекте
|
|
О проекте



 ro
ro  r
r  logarithmic capacity
logarithmic capacity